Redução de Dimensionalidade

Ao incluirmos mais atributos no estudo das observações, podemos estar a degradar a performance do modelo. Para além disso, o número de observações de treino necessárias cresce exponencialmente com a dimensão das observações. De modo a aprender num domínio de elevada dimensão e onde existem poucas observações, procede-se ao processo da redução de dimensionalidade.

Estando perante pontos pertencentes a $\mathbb{R}^{m}$, o objetivo é transformá-los em pontos pertencentes a $\mathbb{R}^{k}$, em que $k << m$, preservando ao máximo a informação e estrutura dos dados originais. A partir dos dados transformados, podemos resolver o problema no novo espaço.

Este processo é realizado através de duas principais abordagens: a seleção de atributos e a extração de atributos.

Seleção de Atributos

Neste processo os novos atributos correspondem a um sub conjunto dos atributos originais. Tipicamente são escolhidos os $k$ melhores atributos, segundo um critério de importância. Entre os critérios encontram-se a entropia de uma variável e o ganho de informação.

Extração de Atributos

Neste processo os novos atributos correspondem a uma combinação ou transformação dos atributos originais. Estas transformações são simples e fáceis de calcular. As principais abordagens realizam transformações lineares sobre os dados originais.

Transformação Karhunen-Loève

Este método é baseado na teoria espectral. O objetivo é diagonalizar a matriz de covariância, fazendo com que toda a variância esteja "alinhada" de acordo com um único eixo do sistema de coordenadas, sendo as variâncias determinadas pelos valores próprios da matriz. Assim, acabamos por "rodar" o sistema de eixos original.

Para tal, calculam-se os valores próprios da matriz de covariância, $\Sigma$ ($k$ por $k$), através da equação abaixo.

Obtidos os $k$ valores próprios da matriz $\Sigma$, procede-se ao cálculo dos vetores próprios. Para cada valor próprio $\lambda_k$, obtemos o vetor próprio correspondente, $u_k$, através da equação seguinte.

Obtidos os vetores próprios, temos a nossa matriz de mudança de base, $U$, que, quando aplicada a um ponto do conjunto de dados original, $x$, nos dá o ponto transformado, $y$, no novo espaço

A matriz $U$ é composta pelos vetores próprios encontrados, em cada uma das suas colunas.

Componentes Principais

Obtidos os valores e vetores próprios da matriz de covariância, podemos inferir algo sobre a variância dos dados. Os vários valores próprios indicam a variância pela qual o atributo que representam é responsável. Assim, temos a seguinte relação

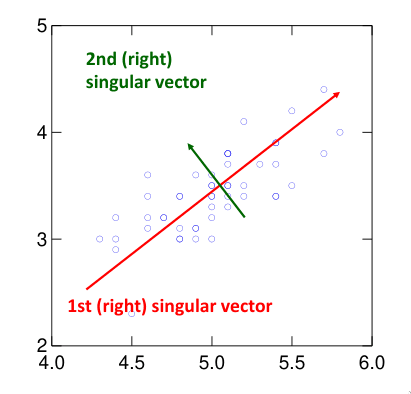
Os vetores próprios de cada componente indicam a direção de máxima variância. O vetor próprio correspondente ao maior valor próprio aponta na direção de máxima variância. O segundo vetor próprio refere a direção de máxima variância, não contando com o primeiro vetor. Este padrão continua para os $N$ vetores próprios. É de notar que os valores próprios são todos perpendiculares entre si.

As componentes principais correspondem aos vetores próprios normalizados. A i-ésima componente principal corresponde ao vetor próprio normalizado, cujo valor próprio é o i-ésimo maior valor. O vetor próprio associado ao maior valor próprio diz-se o vetor próprio mais significante.

Principal Component Analysis

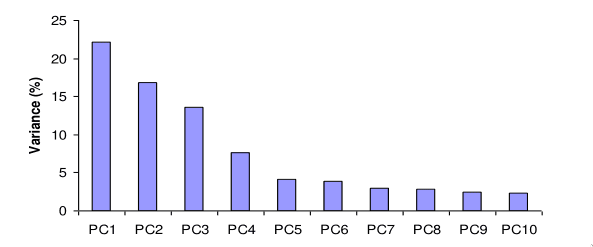
O algoritmo de PCA baseia-se no facto de a variância ser explicada pelos valores e vetor próprios e efetua a redução de dimensionalidade desejada. Tipicamente, é fixado um valor de variância que se deseja obter no novo conjunto de dados, tipicamente $\geq 85\%$. A partir desse valor, são mantidas as componentes principais necessárias para explicar esse valor de variância. Muitas vezes, uma grande parte da variância é explicada por um pequeno número de componentes.

Critério de Kaiser

O critério de Kaiser refere que devem ser descartadas as componentes principais que tenham um valor próprio menor do que 1.