Regressão Linear
Regressão Simples
A equação da reta no plano é dada pela seguinte expressão.
Podemos extender o conceito a mais dimensões, obtendo a equação de um hiperplano.
A ordenada na origem, , tem o nome de bias, pois está influenciado de forma a tender para na ausência de algum input. Damos a cada valor de o nome de peso, sendo o vetor de pesos.
De modo a simplificar a expressão, adiciona-se um termo ao vetor .
Erro Quadrático Médio
Dada um conjunto de treino, ao qual se aplica a regressão, este é composto por um vetor de observações e por um vetor de rótulos, .
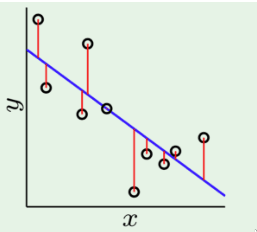
É possível quantificar o erro através das distâncias entre cada observação, representada por um ponto em , e o hiperplano da regressão. As linhas vermelhas na figura abaixo correspondem à função de resíduos, dada pela diferença .
Definimos a função do erro quadrático médio como
Ao comparamos diferentes hiperplanos, podemos guiar-nos pela métrica do erro quadrático médio. Contudo, dividir por ou por qualquer outro número não fará diferença na comparação entre os hiperplanos. Ao derivarmos a função de erro, a constante "corta" com a derivada do quadrado, originando uma expressão "bonita" para o gradiente do erro. Assim, tomamos a chamada half squared error loss como
Design Matrix e Vetor de Rótulos
Definimos a matriz como a design matrix, resultante dos dados adicionando um termo de bias a cada linha . O vetor é o vetor de rótulos das observações.
Assim, a regressão utiliza os pesos de modo a mapear as entradas em saídas.
Solução Fechada
Muitas das vezes um mapeamento linear perfeito das entradas para saídas não existe, devido a ruído nos dados. De modo a encontrar o melhor hiperplano, necessitamos de minimizar o erro , calculando o gradiente e igualando-o a 0. Definido a matriz como a design matrix, chegamos a uma solução fechada para o vetor de pesos, .
Matriz de Moore-Penrose
A matriz , derivada na solução fechada é conhecido como a pseudo-inversa de ou matriz de Moore-Penrose. Assim, a solução fechada pode ser dada por .
A matriz não é invertível quando alguns atributos são combinações lineares uns dos outros ou quando existem mais atributos do que observações. No entanto, a pseudo-inversa está sempre definida.
Transformações do Conjunto de Dados
Por vezes, o conjunto de dados não consegue ser modelado por uma regressão linear, sendo necessária uma regressão mais expressiva. De modo a solucionar este problema, podemos aplicar uma transformação ao conjunto de dados original, reescrevendo cada um dos atributos como uma transformação não linear do mesmo. Assim, realizamos uma regressão linear ao novo conjunto de dados transformado.
em que representa uma transformação não linear à entrada . Esta função é conhecida como basis function.
Assim, realizamos a regressão com a nova design matrix.
É de notar que a regressão linear sem a transformação do conjunto de dados corresponde a uma transformação de atributos realizada pela basis function .
Seleção do Modelo
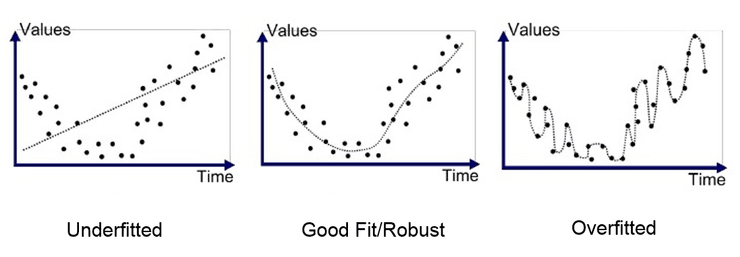
É de notar que entre dois polinómios de diferentes graus, o polinómio com maior grau tem um maior poder expressivo pois consegue modelar qualquer relação que o polinómio de grau mais baixo consegue. Assim, seria de esperar que ao realizar uma regressão num conjunto de dados para os quais não sabemos o polinómio gerador, seria melhor utilizar um polinómio com o maior poder expressivo possível.
Contudo, ao adicionar algum ruído aos dados, o polinómio com maior poder expressivo afasta-se bastante do polinómio gerador, enquanto que o polinómio com menor poder expressivo, limitado, consegue lidar melhor com a presença de outliers. Assim a escolha de um polinómio com a complexidade certa (não muito baixa, nem demasiado alta) é essencial para evitar o problema de overfitting.
Regressão Bayesiana
O conhecido classificador de Bayes pode também ser usado para tarefas de regressão. Procuramos descobrir o vetor de pesos mais provável para a evidência que temos, o conjunto de dados . corresponde ao prior e corresponde à likelihood.
Assim, definimos o vetor de pesos, , de máxima verosimilhança (maximum likelihood) como
Outra abordagem passa por maximizar , a posteriori, onde a likelihood é multiplicada pelo prior.
Solução Fechada
O objetivo é, então, calcular a distribuição de probabilidade . Chegamos à expressão seguinte.
Assume se que os exemplos são independentes e identicamente distribuídos e que o erro da regressão linear . Assim, . Obtemos então a seguinte relação.
Derivando a expressão anterior e igualando-a a 0, obtemos a seguinte solução fechada.
Se, por outro lado, realizarmos o mesmo processo para o vetor de pesos de máxima verosimilhança, obtemos a seguinte solução fechada.
Regularização
Regressão de Ridge
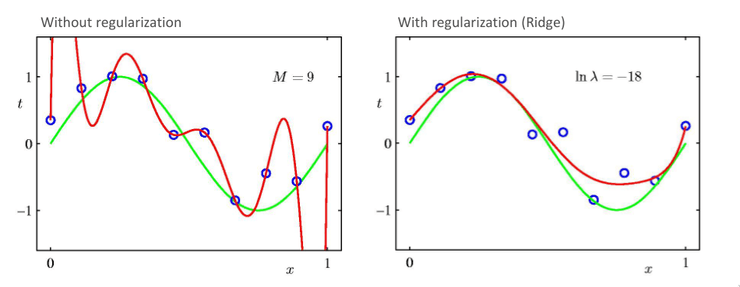
Como verificado anteriormente, polinómios com elevado valor expressivo que minimizam o erro quadrático encontrado tendem a criar modelos que sofrem de overfitting. De modo a resolver este problema, é adicionado um termo à expressão do erro, que penaliza modelos em que os valores dos pesos são muito elevados. É um facto experimental que regressões com valores pequenos de pesos produzem modelos que evitam o overfitting.
Este regularizador tem o nome de regressão de Ridge. Mais uma vez, podemos igualar a 0, encontrando a solução fechada para a regressão de Ridge.
Podemos verificar que a solução encontrada é idêntica ao estimador maximum a posteriori!
O termo de regularização descreve o quociente de duas variâncias.
Regressão de Lasso
Uma alternativa ao termo do regularizador quadrático de Ridge é o termo linear de Lasso. Esta alternativa difere do regularizador quadrática ao assumir que o erro segue uma distribuição de Laplace, ao invés de uma distribuição normal.
Contudo, este regularizador não apresenta uma solução fechada, pois o termo não é diferenciável na origem. Contudo, uma solução não fechada pode ser obtida através de outros métodos, como gradient descent. Este regularizador tende a gerar soluções mais esparsas (com mais zeros no vetor de pesos) do que o regularizador de Ridge.
Overfitting
De modo a evitar o overfitting, pode ser utilizada uma regressão com um termo de regularização, como os regressores de Ridge e Lasso.