Avaliação de Modelos

Overfitting

Quando um modelo se adapta demasiado aos dados de treino, não conseguindo rotular com sucesso objetos ainda não observados, estamos perante um modelo em overfitting.

Este fenómeno ocorre porque os dados de treino, apesar de conterem as regularidades da população, contêm também erros de amostragem. Ao ajustar o modelo aos dados, o algoritmo não consegue identificar estas irregularidades. O modelo é, então, enviesado para os dados de treino, memorizando os dados de treino, em vez de os aprender.

De modo a evitar este fenómeno, podemos dividir os dados de treino em vários subconjuntos, desde que todos eles mantenham a distribuição original dos dados. Realizada a partição, utilizam-se alguns dos subconjuntos para aprender e treinar o modelo e usamos outros para escolher o melhor modelo encontrado, aquele que apresente o melhor desempenho.

Algumas estratégias para evitar o overfitting passam por:

• De acordo com o princípio da Occam's Razor, na presença de dois modelo com desempenho semelhantes, escolher o mais simples.
• Usar conjuntos de treino e teste independentes entre si.
• Treinar com recurso ao conjunto de treino e escolher o melhor modelo com base num conjunto de validação.

Estratégias de Treino

Hold-Out

Quando estão disponíveis vários milhares de dados, dividimos este conjunto em dois subconjuntos (sempre que possível manter a distribuição original dos dados): o conjunto de treino e o conjunto de teste, normalmente numa proporção $70/30$. Contudo, ficamos com uma estimativa enviesada se escolhermos o modelo que apresenta melhor desempenho. Para solucionar isto, a partir do subconjunto de teste é criado o conjunto de validação, utilizado para escolher o melhor dos modelos. Finalmente, a exatidão do modelo é avaliada no conjunto de teste.

Leave-One-Out

Esta estratégia de treino é utilizada quando temos poucos registos com que aprender. Usualmente, o conjunto de teste é formado por apenas um registo, utilizando o resto dos registos para treinar o modelo. Este processo é repetido para cada um dos registos, criando tantos modelos quanto o número de registos. No final, a performance do modelo é avaliada com o número de registos classificados corretamente.

Cross-Validation

É uma estratégia de treino utilizada quando temos acesso a poucos milhares de registos e não conseguimos garantir a manutenção da distribuição do conjunto de dados ao proceder à sua divisão.

Através do conjunto de dados total, geram-se $k$ subconjuntos mutuamente exclusivos, com tamanhos semelhantes, mantendo a distribuição da classe dos dados originais (validação cruzada estratificada).

Utilizamos cada conjunto para avaliar o modelo aprendido pelos outros $k-1$ subconjuntos.

• Treina-se em $D_2 \cup D_3 \cup D_4$ e valida-se em $D_1$.
• Treina-se em $D_1 \cup D_3 \cup D_4$ e valida-se em $D_2$.
• Treina-se em $D_1 \cup D_2 \cup D_4$ e valida-se em $D_3$.
• Treina-se em $D_1 \cup D_2 \cup D_3$ e valida-se em $D_4$.

À semelhança da estratégia de leave-one-out, são gerados vários modelos. O processo é repetido várias vezes, de modo a aumentar a confiança nos resultados obtidos.

Avaliação

Avaliar o desempenho dos modelos é uma tarefa importante, pois nos permite dizer qual destes é o mais indicado a usar.

Com vários modelos possíveis que se ajustam aos conjunto de dados, muitas das vezes apenas podemos escolher um. Mas qual escolher? Este é problema da seleção do modelo. De modo a resolvê-lo analisam-se várias propriedades dos modelos em questão, com o objetivo de encontrar aquele que, de facto, melhor se adapta aos dados.

Matriz de Confusão (Confusion Matrix)

Considere-se um modelo de classificação $M: A \mapsto C$, como uma função que mapeia um conjunto de variáveis a um rótulo ou classe.

O modelo é treinado contra um conjunto de dados rotulados, o conjunto de treino. A informação resultante da classificação do conjunto de teste pode ser representada numa matriz de confusão. Cada linha da matriz representa as instâncias da classe real dos dados do conjunto de treino, enquanto que as colunas da matriz representam as classes atribuídas pelo modelo, durante o processo de classificação.

Exatidão e Erro

A partir da informação representada na matriz de confusão, podemos definir algumas medidas importantes.

A análise destas métricas, sem outros dados, constitui alguns problemas. A exatidão (accuracy) não indica qual o tipo de erro mais frequente (falsos positivos ou falsos negativos), que em muitos domínios precisam de ser diferenciados. Além disso, a exatidão é enviesada para um valor maior se o conjunto de treino for constituído maioritariamente por observações pertences a uma das classes.

Precision, Recall e Fallout

De modo a solucionar os problemas descritos acima, introduzem-se mais medidas.

O recall ou sensitivity indica a percentagem de observações positivas classificadas como positivas.
O fallout ou specificity indica a percentagem de observações negativas classificadas como negativas.
A precision indica a percentagem de observações positivas entre as observações classificadas como positivas.

Um elevado valor de recall sem uma boa precision não nos dá confiança acerca da qualidade da classificação. É possível obter um elevado valor de recall classificando todos os registos como positivos. Contudo, o valor de precisão será bastante baixo. Por outro lado, ao classificar apenas um registo como positivo, obtemos uma precisão máxima, mas um baixo valor de recall. Ao avaliar um modelo, temos de ter em conta estas duas medidas. Para isso, definimos uma nova medida, a F-measure ou medida de balanço, dada por uma média harmónica ponderada.

Normalmente, a medida mais utiliza é F1 measure, onde $\beta$ toma o valor 1.

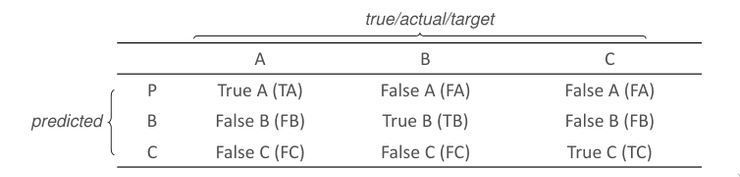
Múltiplas Classes

Na maior parte das tarefas de classificação, existem mais do que duas classes. Nesses casos, podemos extender o conceito da matriz de confusão para classificações não binárias.

As medidas tomam agora valores por classe: a classe principal é vista como positiva, enquanto que as restantes são vistas como negativas.