Estudo Gráfico de Funções

Assíntotas

Assíntotas Verticais

Diz-se que a reta de equação $x=x_0$ é uma assíntota:

• vertical à esquerda para $f$ se $f$ está definida em $]x_0 − r, x_0[$, para algum $r\in\R^+$, e $f(x_0^-)=\pm \infin.$
• vertical à direita para $f$ se $f$ está definida em $]x_0, x_0+r[$, para algum $r\in\R^+$, e $f(x_0^+)=~\pm \infin.$
• bi-lateral para $f$ se é simultaneamente uma assíntota à esquerda e uma assíntota à direita.

👉 Só é preciso estudar a existência de assíntotas verticais nos pontos em que a função não é contínua.

Podem existir infinitas assíntotas verticais numa função, tal como é o caso da função $f(x)=\tg x.$

Exemplos

Exemplo 1

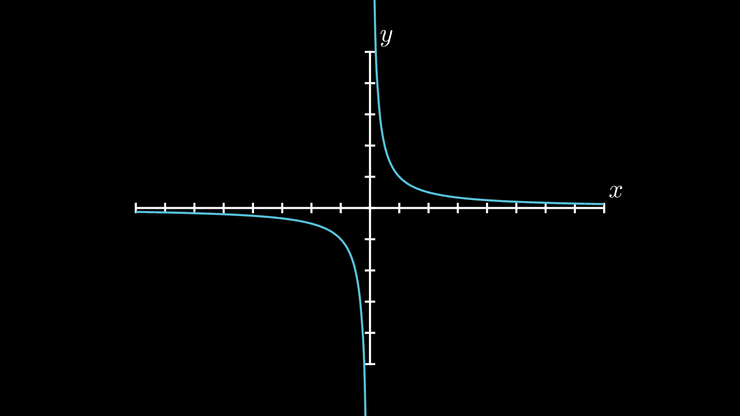
Função $f:\R\backslash \{0\}\to \R\quad,\quad f(x)=\frac 1x$

Tem uma assíntota bi-lateral de equação $x=0$.

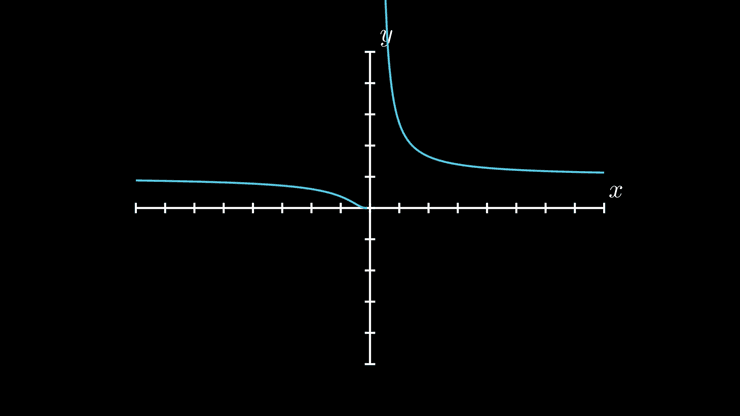
Exemplo 2

$$g:\R\to\R\quad,\quad g(x)=\begin{cases} e^{\frac 1x} &\text{se }x\ne 0\\ 0&\text{se }x=0 \end{cases}$$

Tem uma assíntota à direita de equação $x=0$. É de salientar que esta função está definida na origem, sendo mesmo contínua à esquerda. Mesmo assim, tem uma assíntota neste ponto.

Assíntotas Não Verticais

Seja $f$ uma função que está definida em $V_r(+\infin)$, para algum $r\in\R^+$.

Diz-se que a reta ${y=m_+x+b_+}$ é uma assíntota não vertical à direita de $f$ se

Também se diz, nesse caso, que a reta descreve o comportamento assintótico de $f$ quando ${x\to+\infin}$.

Define-se de modo equivalente uma assíntota não vertical à esquerda de $f$, ${y=m_{-}x+b_{-}}$.

👉 Caso $m$ ou $b$ não pertençam a $\R$, não existe assíntota não vertical (no "lado" que estiverem a verificar).

Pela unicidade do limite, existe no máximo, uma assíntota não vertical à esquerda e uma assíntota não vertical à direita.

Assíntotas Não Retilíneas

A explicação de como determinar assíntotas não retilíneas (não verticais) encontra-se nas páginas 3 e 4 do PDF da aula 19. Entre outros, exemplos destas assíntotas são assíntotas quadráticas e assíntotas exponenciais.

Paridade de funções

Seja $D_f\subset\R$ um conjunto simétrico e $f: D_f\to \R$ uma função definida em $D_f$. Diz-se que

• $f$ é uma função par se $f(-x)=f(x)$ para todo o $x\in D_f$. Também se diz, nesse caso, que $f$ é simétrica em relação ao eixo $x=0$.
• $f$ é uma função ímpar se $f(-x)=-f(x)$ para todo o $x\in D_f$. Também se diz, nesse caso, que $f$ é simétrica em relação à origem.
• $f$ é uma função simétrica se $f$ é par ou $f$ é ímpar.

Simetria em relação a $x_0$

Também é possível estudar a simetria num eixo sem ser $x=0$ ou num ponto sem ser a origem.

Uma função definida num conjunto $D_f$ simétrico em relação a $x_0$ é simétrica em relação ao eixo $x=x_0$ se $f(2x_0-x)=f(x)$ para qualquer $x\in D_f$.

Uma função definida num conjunto $D_f$ simétrico em relação a $x_0$ é simétrica em relação ao ponto $(x_0,y_0)$ se $f(2x_0-x)=2y_0-f(x)$.

Exemplo

Tenhamos

$$f :] − \infty, 0] \cup [2, +\infty[\to \R , f(x) = \sqrt{x^2 - 2x}.$$

É fácil verificar que, sendo $D_f =] − \infty, 0] \cup [2, +\infty[$,

$$x \in D_f \implies 2 − x \in D_f$$

e que $f(2 − x) = f(x)$ ou, mais simplesmente que a função $g$ definida por

$$g(x) = f(x + 1) = \sqrt{x^2 - 1}$$

é uma função par de domínio $\R \backslash ] − 1, 1[.$
Se, por exemplo, se calcular $f(2^+)$ tem-se, de imediato e sem mais cálculos, que $f(0^−) = f(2^+)$. Esta simplificação não é muito interessante, mas supondo que se pretende determinar as derivadas laterais nos ponto 0 e 2, o que tem que ser feito pela definição, o resultado já é mais interessante. Tem-se

$$f'_d(2) = \lim_{x\to 2^+} \frac{f(x) − f(2)}{x - 2} = \lim_{x \to 2^+} \frac{\sqrt{x(x-2)}}{x-2} = \lim_{x \to 2^+} \sqrt{\frac{x}{x-2}} = +\infty.$$

Para calcular $f'_e$ usando a definição ter-se-ia que fazer algo semelhante mas tendo cuidado com o passar $x$ para dentro da raiz que daria origem ao aparecimento de um sinal negativo no exterior da raiz,

$$f'_e(0) = \lim_{x\to 0^-} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0^-} \frac{\sqrt{x(x-2)}}{x} = \lim_{x \to 0^-} - \sqrt{\frac{x-2}{x}} = - \infty.$$

Usando a simetria, como a derivada de uma função par é ímpar, ter-se-ia, simplesmente,

$$f'_e(0) = −f'_d(2) = −\infty.$$

Periodicidade

Estudo Completo de uma Função

O estudo completo de uma função consiste nos seguintes passos:

1. Domínio, simetria e periodicidade. Neste ponto podem ainda incluir-se as interseções com os eixos. Caso haja simetria ou periodicidade, esse facto deverá afetar o estudo seguinte, simplificando-o.
2. Continuidade e assíntotas. Aqui deve incluir-se o estudo da existência e prolongamento contínuo aos pontos de $\overline{D_F}\backslash D_F$. Caso exista prolongamento contínuo em algum desses pontos o restante estudo deve incidir sobre esse prolongamento.
3. Diferenciabilidade, monotonia e extremos.
4. Diferenciabilidade da derivada, concavidade e inflexões. Aqui é útil incluir a determinação do declive da tangente nos pontos de inflexão.
5. Gráfico e contradomínio. Aqui é útil começar por elaborar um quadro resumo de todo o conhecimento obtido sobre a função.

Das páginas 8-10 da Aula 19 encontra-se o estudo completo da função

que é bastante importante ver.

---

PDFs:

• Aula 19