Noções topológicas
Conjunto numerável e contável
DEFINIÇÃO
- Conjunto numerável: Diz-se que é um conjunto numerável se existe uma bijeção de em .
- Conjunto contável: Um conjunto é contável se for finito ou numerável.
É de salientar que os conjuntos , e são, embora infinitos, numeráveis e, consecutivamente, contáveis. No entanto, não é numerável.
Densidade dos racionais: Em qualquer intervalo de números reais existem números racionais e irracionais (na verdade um número infinito de cada um deles).
Vizinhanças
DEFINIÇÃO
Vizinhança de raio de um ponto :
Seja e , chama-se vizinhança de raio de ao conjunto
Interior, exterior, fronteira e fecho de um conjunto
Seja . Diz-se que:
- é um ponto interior de se existe uma vizinhança de contida em
- é um ponto exterior de se existe uma vizinhança de que não contém pontos de
- é um ponto fronteiro de se em qualquer vizinhança de existem pontos de e pontos que não são de
- é um ponto aderente a se em qualquer vizinhança de existem pontos de , isto é, são pontos do interior ou da fronteira de .
Chama-se:
- Interior de , , ao conjunto dos pontos interiores de
- Exterior de , , ao conjunto dos pontos exteriores de
- Fronteira de , , ao conjunto dos pontos fronteiros de
- Fecho ou aderência de , , ao conjunto dos pontos aderentes a
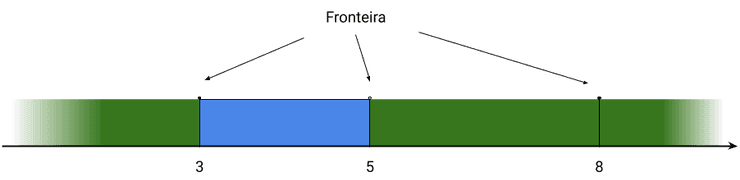
Exemplo
Abaixo está a representação do conjunto . A zona representada a azul corresponde ao interior de , enquanto que a zona a verde corresponde ao exterior de .
Conjunto Aberto. Conjunto Fechado. Conjunto Compacto
Seja , diz-se que:
- é aberto se
- é fechado se
- é compacto se é fechado e é limitado
Exemplos de conjuntos abertos, fechados e compactos estão no PDF em anexo.
Existem dois casos em que um conjunto pode ser simultaneamente aberto e fechado: e .
Ponto de Acumulação. Ponto Isolado. Derivado de um Conjunto
Seja um conjunto e . Diz-se que é um ponto de acumulação de se existem pontos de diferentes de e arbitrariamente próximos de , ou seja, se dado qualquer raio : .
A qualquer ponto de que não seja um ponto de acumulação de chama-se ponto isolado.
Ao conjunto dos pontos de acumulação de chama-se derivado de e representa-se por .
PDFs: