Algoritmo de Kuratowski
Definições
Subdivisão de um grafo
Consiste em adicionar um número de vértices qualquer ao longo de arestas quaisquer do grafo.
Grafos Isomorfos
Um grafo é isomorfo de um grafo se existe uma aplicação que coloca cada vértice do grafo no grafo , preservando as arestas.
Grafos Equivalentes
Dois grafos e são equivalentes se são isomorfos e preservam as fronteiras.
Exemplos
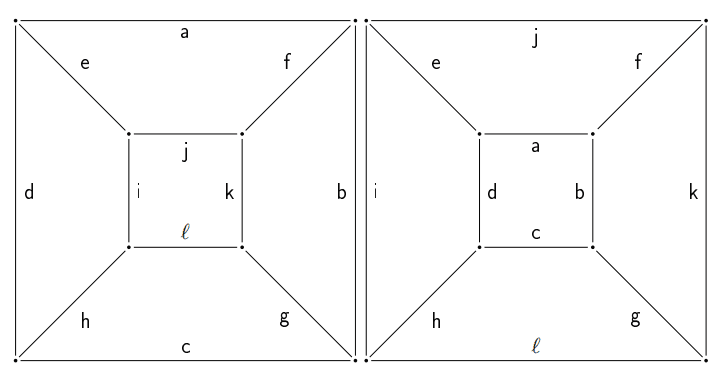
Representação Grafo Planar
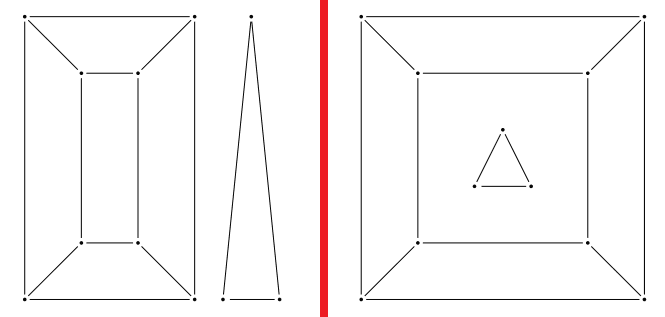
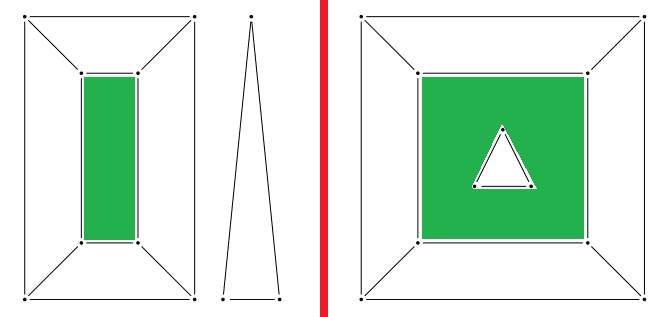
Um grafo é planar, se e só se conseguirmos representá-lo numa superfície esférica, tal que os seus vértices não se intersetem.
As projetarmos o desenho num plano, ficamos com uma representação do grafo planar.
Se rodarmos a esfera e projetarmos outra vez, teremos um desenho de um novo grafo planar, equivalente ao inicial.
Importante
Ao rodarmos a esfera sobre os eixos, conseguimos obter todas as representações do grafo planar.
Redução de um Grafo
Reduz-se um grafo, quando eliminamos um vértice de grau . Se eliminarmos , cujas arestas eram e , essas arestas desaparecem e aparece um nova:
Grafo Homeomórfico
Dois grafos são homeomórficos se conseguimos aplicar a redução, até os grafos ficarem iguais.
Teorema de Kuratowski
Um grafo é planar se e só se não contém um subgrafo homeomórfico ao grafo ou ao grafo .
Relembrar
- Grafo Completo de 5 vértices$
- Grafo bipartido com partições de dimensão