Autómatos Finitos
Pequeno Exemplo
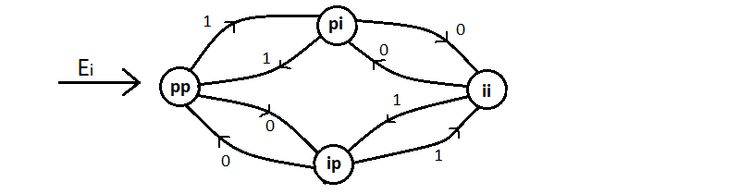
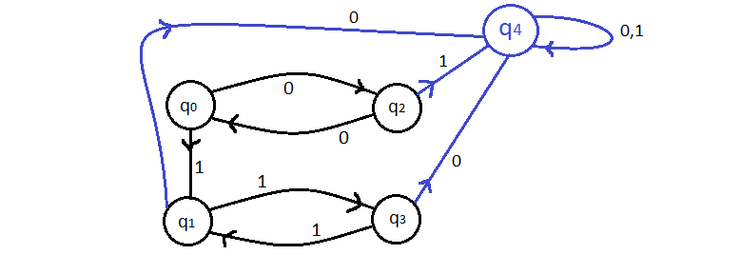
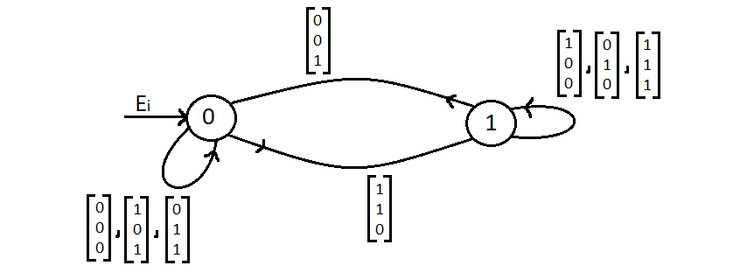
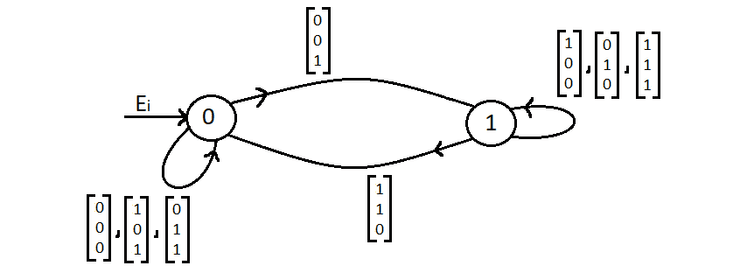
Representação gráfica de um autómato que, numa palavra de 's e 's finita, verifica se o número de 's é par e 's é ímpar.
Onde é par, ímpar e primeiro referimo-nos aos 's e depois aos 's.
"Ei" aponta para o estado inicial.
Autómato Finito Determinístico (AFD)
Um autómato finito determinístico é um quíntuplo onde:
- é um conjunto finito não vazio
- é o estado inicial do autómato
- é um alfabeto (conj. finito de símbolos)
- estados de aceitação/finais
- função que, com o estado atual e com que recebe, transita para um novo estado
Exemplo 1
Pegando no exemplo do início onde queríamos verificar se, numa palavra de 's e 's, o número de 's é par e 's é ímpar.
Relembrar que queríamos ver se a palavra tinha um número par de 's e ímpar de 's, por isso é que .
Exemplo 3
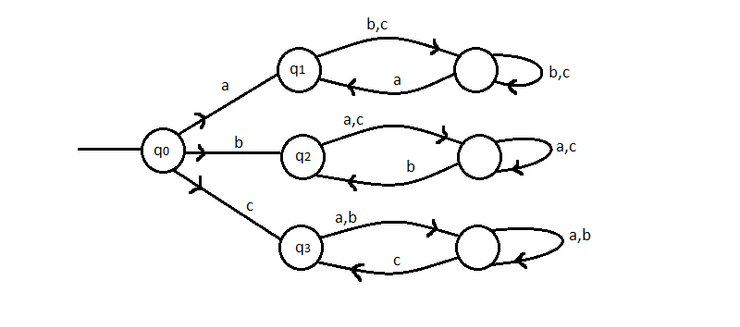
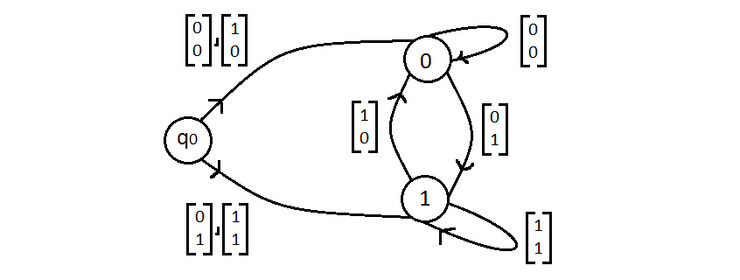
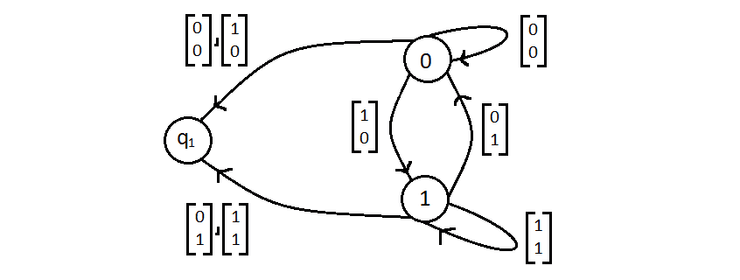
Queremos um AFD que receba palavras formadas por e que verifique se começa e acaba na mesma letra.
Neste exemplo, mostra-se apenas a representação gráfica.
IMPORTANTE
Podemos definir ainda , como sendo a função que recebe um estado e uma palavra. Pode ser definida recursivamente como:
Aceitação de um AFD
Diz-se que um AFD aceita a palavra se (O estado a que chegamos no final pertence aos estados de aceitação)
Linguagem reconhecida
A Linguagem (ou conjunto) reconhecido (ou decidido) pelo AFD é o conjunto (conjunto de palavras que o AFD aceita).
Linguagem Regular
Uma Linguagem diz-se Regular se existir um AFD que a reconheça.
Autómato Completo
Até agora, os exemplos vistos foram todos de Autómatos Completos, ou seja, para cada estado temos indicação para mudar de estado para todo o "input" recebido.
Há casos onde isto não acontece, e aí estamos perante um Autómato Não Completo (ANC).
Exemplo Importante - ANC
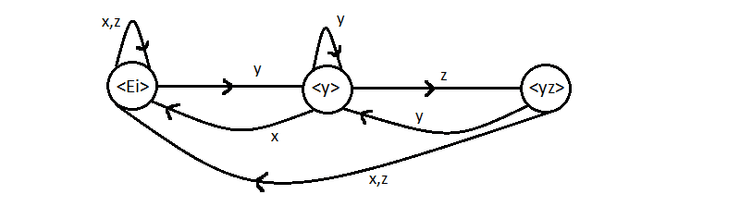
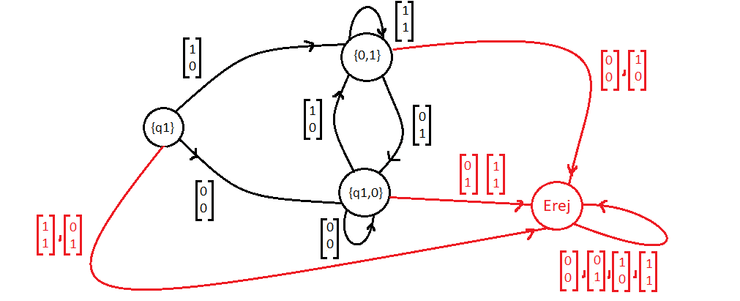
Queremos um autómato que recebe uma palavra de 's e 's e verifica se a palavra é constituída primeiro por um número par de 's e depois por um número par de 's. Por exemplo, é aceite, mas não é.
Seja o estado inicial e
Repare-se que não está especificado o que acontece se estivermos em e recebermos um , tal como em , e em se receber .
Não é sem querer que isso acontece apenas nesses casos, de facto nessas situações a palavra seria logo "não aceite".
Nos ANC, omitimos um estado onde vai parar tudo o que não está especificado, o Estado de rejeição.
NOTA
Para encontrar o complementar do autómato descrito acima, teríamos de incluir o estado omitido, porque é necessário nessa situação.
Autómato Finito Não Determinístico (AFND)
Um AFND é um quíntuplo , onde:
- é um conjunto finito não vazio
- é o estado inicial do autómato
- é um alfabeto (conj. finito de símbolos)
- estados de aceitação/finais
- função que, com o estado atual e com que recebe, pode transitar para um conjunto de estados , onde é o conjunto dos subconjuntos de
NOTAS
-
Um
AFNDé feito sabendo que tem de haver pelo menos um caminho para as palavras aceitáveis e nenhum para as que não são. -
Após aplicar um
AFNDuma vez, este não classifica uma dada palavra como aceite ou não aceite.Caso a palavra seja aceite pelo
AFNDé aceite, mas se não for, considera-se que pode (ou não) ser. -
Pode ter mudanças de estado , podem acontecer ou não. (Existe Exemplo mais à frente )
Exemplo 1
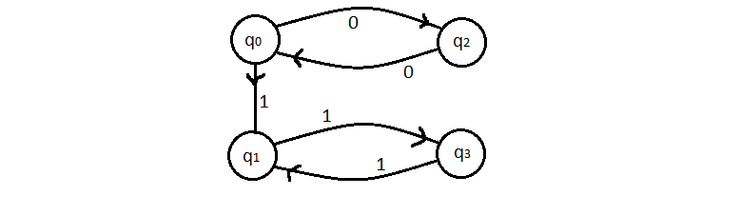
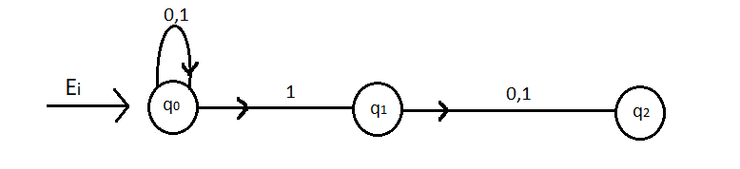
AFND para calcular se uma palavra constituída por 's e 's tem um na penúltima posição.
Este autómato não é completo
IMPORTANTE
Tal como nos AFD, nos AFND podemos definir ainda , como sendo a função que recebe um estado e uma palavra e que define a que conjunto de estados podemos acabar no final da palavra. Pode ser definido por:
Onde:
-
Ao aplicarmos a um estado e se não recebermos nada, poderá transitar para todos as transições do estado . Estes estados são representados por .
-
Ao aplicarmos a um estado quando recebe uma palavra , onde é o último símbolo da palavra e , o estado final será o resultado de aplicar , quando recebe a letra , a todos os estados a que podemos chegar quando recebemos a palavra . Não esquecendo as transições .
Aceitação AFND
Diz-se que um aceita a palavra se
Linguagem Reconhecida
A Linguagem Reconhecida por um AFND será:
Teorema 1
Qualquer que seja o AFND , existe um AFD que lhe é equivalente, ou seja as Linguagens Reconhecidas são iguais.
Passar de AFND para AFD
Exemplo
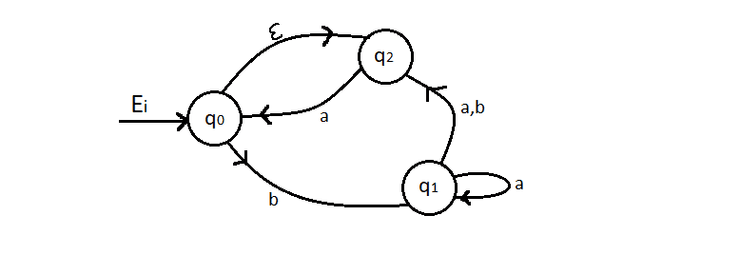
Temos o seguinte AFND
Repare-se que temos uma "transição ", ou seja, pode acontecer do nada. Deste modo, o estado inicial tanto pode ser ou .
Como fazemos para encontrar o AFD?
-
Cria-se um estado que albergue todos os estados iniciais (neste caso e )
-
Depois, dependendo do input que podemos receber (neste caso ou ) "apontamos" para um novo estado. Se não existir cria-se.
Atenção: o novo estado, tal como no estado inicial, pode ser um "conjunto de estados" -
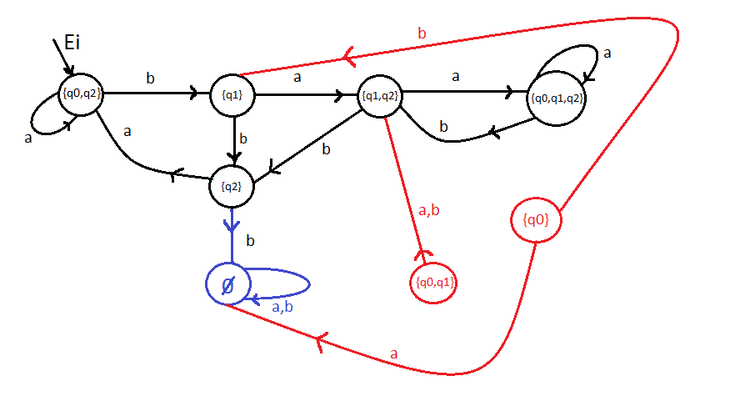
Se temos estados no
AFNDteremos no máximo noAFD(os vários conjuntos possíveis formados pelos estados doAFND), contudo pode haver estados inúteis (a vermelho abaixo). São estados a que nunca chegamos se partirmos do início. Podem ser omitidos na representação final
Atenção: Não esquecer do estado de rejeição se for necessário (abaixo está a azul)
Segue-se a representação final, com um pequeno exemplo de uma parte da execução abaixo
- Começamos nos estado que engloba os estados iniciais e
- Quando estamos em ou e recebemos , vamos sempre para . Se recebermos , tanto podemos ir para ou para , por causa da transição .
- Quando estamos em e recebemos , vamos para , mas por causa da transição , podemos voltar a . Por isso, se recebermos em continuamos no mesmo estado.
Repare-se que os estados inúteis (vermelho), nunca são atingidos desde o Ei.
Operações da Esquerda para a Direita - Autómatos
Para fazer uma operação da esquerda para a direita com autómatos (por exemplo: soma, divisão, ), basta fazer um autómato que faça a operação da direita para a esquerda e depois trocar as transições e os estados de aceitação com o estado inicial.
Para além disso, também pode ser necessário passar de um AFND para um AFD.
Exemplo 1 - Soma
Vamos definir a soma da esquerda para a direita, com
Por exemplo,
Primeira faz-se o autómato da soma da direita para esquerda
Os estados e simbolizam os restos.
e ( é o estado inicial e o de aceitação).
Agora trocamos os estados de aceitação e inicial (como é o mesmo, não trocamos), por isso apenas se trocam as transições entre estados.
Como é um AFD já é o resultado final
Relembrar
As transições não representadas, em ambos, são as transições para o estado de rejeição.
Exemplo 2 - Divisão por 2
Vamos definir a Divisão por 2 da esquerda para a direita, com
Por exemplo,
Primeira faz-se o autómato da Divisão por 2 da direita para esquerda.
Agora, para obtermos a operação da esquerda para a direita fazemos as trocas necessárias.
Agora temos que e .
Temos um AFND. Precisamos de passar para um AFD.
Neste último autómato está representado o estado de rejeição a vermelho
Propriedades
Teorema 2
O complementar de uma Linguagem Regular (LR), a interseção de duas LR e a união de duas LR também são Linguagens Regulares.
Exemplo - Complementação
O seguinte autómato serve para encontrar palavras formadas por que acabem em , onde .
A única diferença entre este e o seu complementar (palavras que não terminam em ) é o , que passa a
Teorema 3
A classe das Linguagens Regulares está fechada para a união, a concatenação e a estrela.
NOTA
Com este Teorema conseguimos construir autómatos maiores/mais complexos, a partir de autómatos mais simples.
União
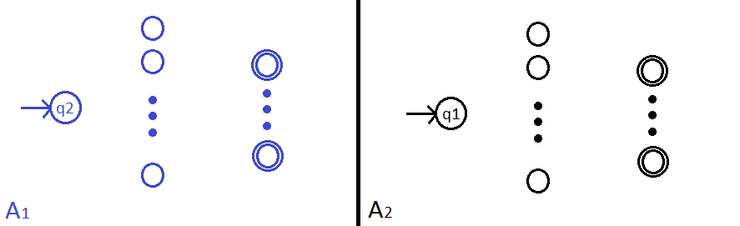
Sejam e dois autómatos diferentes, cuja representação, omitindo as transições e com estados de aceitação duplamente identificados, é a seguinte:
Seja e , (relembrar que é a linguagem de aceitação do autómato )
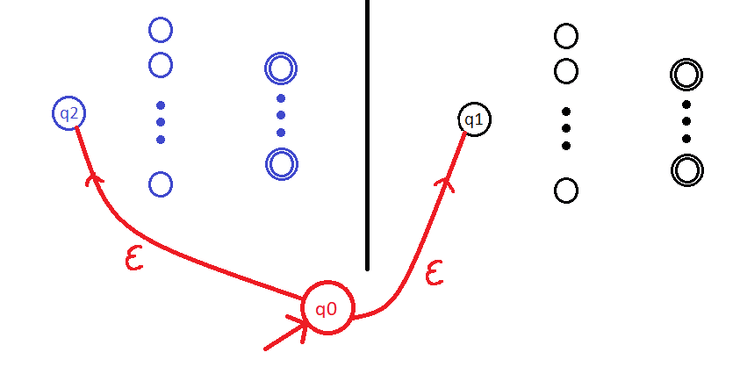
Para representar o autómato de linguagem reconhecida basta adicionar um novo estado inicial que se liga aos estados inicias de e por transições .
Esta última representação é de um AFND, para passar para AFD é só aplicar o algoritmo.
Concatenação
Sejam e dois autómatos diferentes, cuja representação, omitindo as transições e com estados de aceitação duplamente identificados, é a seguinte:
Seja e ,
Por exemplo, concatenação de dois autómatos. Um que aceita um número par de 's e a palavra nula e outro que aceita um número ímpar de 's.
O autómato final aceita apenas uma sequência de 's à direita e 's à esquerda, onde há um número par 's de e ímpar de 's.
Para representar o autómato de linguagem reconhecida basta adicionar transições , que ligam os estados de aceitação de ao estado inicial de .
O estado inicial é o estado inicial de e os de aceitação são os de .
Esta representação é de um AFND, para passar para AFD é só aplicar o algoritmo.
Estrela
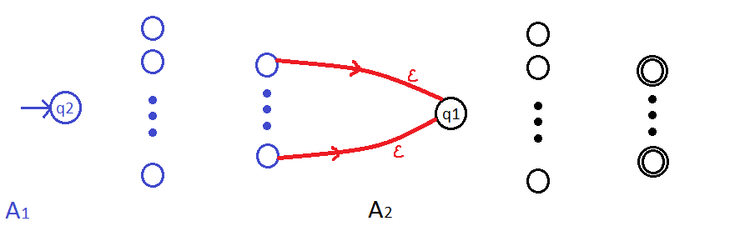
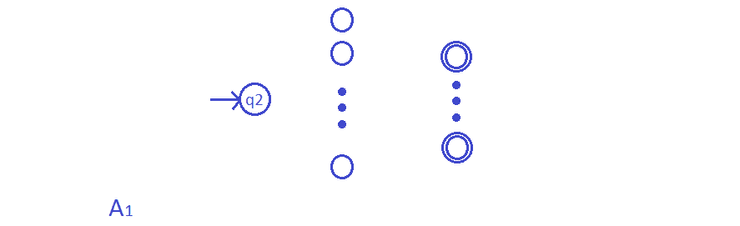
Seja um autómato, cuja representação, omitindo as transições e com estados de aceitação duplamente identificados, é a seguinte:
Seja ,
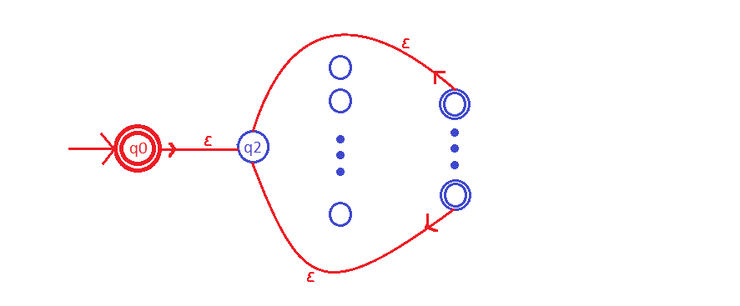
Para representar o autómato de linguagem reconhecida adicionamos um novo estado inicial, que também é de aceitação (para aceitar a palavra nula) e transições como representado abaixo.
NOTA
Também podemos chamar Fecho de Kleene à operação Estrela.
Teorema de Kleene
Uma linguagem é regular se e só se pode ser obtida a partir de conjuntos finitos por união, concatenação e/ou estrela.
NOTA
Seja uma palavra, representa o tamanho da palavra
Lema de Pumping
Se é uma linguagem regular, então existe tal que toda a palavra de tamanho , pode ser subdividida em subpalavras, de tal modo que
Demonstração
é uma linguagem regular, onde , com .
Seja e uma palavra de , onde .
Quando o autómato recebe a palavra lê letras e passa por estados, abaixo encontra-se uma pequena representação desta leitura
Como a palavra é maior ou igual ao número de estados, como mencionado, se visita estados terá de repetir pelo menos um estado (aplicação direta do Princípio de Pombal).
Sejam a primeira vez que se repete um estado, o estado .
Podemos dividir a palavra em partes: , e , onde .
- , as primeiras letras da palavra (antes de chegarmos a )
- , da letra na posição até à posição (antes de chegarmos a )
- , o resto da palavra a partir da letra na posição .
Com esta divisão, retiramos as conclusões finais
- , porque ainda não se repetiu estados
Exemplo - Provar que não é regular
Com o alfabeto , será que existe uma Linguagem Regular apenas aceita palavras com 's à esquerda, 's à direita, onde existe o mesmo número de 's e 's
Vamos supor que a linguagem é regular e vamos tentar verificar todas as condições do Lema de Pumping:
Como é regular tem de existir um tal que todas as palavras com tamanho igual ou superior a podem ser decompostas em subpalavras , tais que:
Se existe um que satisfaz as condições acima, então a palavra
Pertence à linguagem e tem de verificar as condições acima, uma vez que .
Dividindo em subpalavras , pelas condições do Lema de Pumping . Deste modo é uma palavra somente constituída por 's. (Relembrar que ).
Segundo o Lema de Pumping, e , assim, terá de ser uma palavra constituída por 's, MAS quando se repete em o número de 's será maior que o número de 's, ou seja .
Chegamos assim a uma Contradição.
Com esta contradição podemos concluir que a linguagem especificada não é regular.