Grafos Planares
Grafos que podem ser desenhados sem que haja interseções de arestas.
Teoremas
Teorema 1
Num grafo conexo planar de vértices, arestas e regiões, então
Demonstração
Por indução Simples
Base
, então o grafo terá apenas vértice e região.
Hipótese de Indução
Substituindo por temos casos:
-
Grafo é uma árvore
Se é uma árvore, sabemos que terá arestas e apenas tem região, logo, por hipótese de Indução: -
Não é árvore, tem pelo menos um ciclo
Removendo uma aresta do ciclo ficamos com arestas. Agora já não temos ciclo, por isso também temos menos uma região (a do ciclo).NOTA é o número de arestas do grafo em análise, por isso é que é verdade pela
Hipótese de Indução.
QED
Teorema 2
Num grafo conexo planar de vértices, tem-se que
Demonstração
Sabe-se que a menor região num grafo planar é limitada por vértices/arestas (um triângulo, que pode ser "torto" (exemplo no fim)).
Deste modo, seja o número de arestas na fronteira da região , o número de regiões e o número de arestas, no mínimo teremos só regiões formadas por triângulos e a soma de regiões será no máximo (repetimos cada aresta vezes)
Como pelo Teorema 1
QED
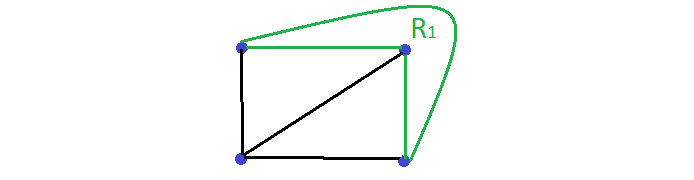
Triângulo "torto"
A região assinalada a verde é limitada por um triângulo ("torto").
Mas atenção: "torto" não foi uma designação dada pelo professor na aula, nem sei se existe.
Exemplo
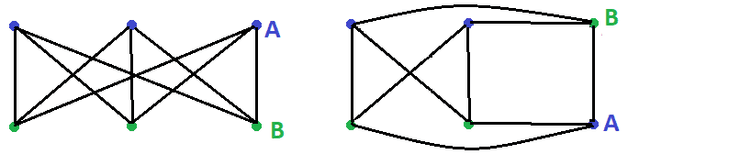
O grafo completo de vértices não é planar.
Como é completo, o número de arestas será
Onde é o número de vértices. Se , e, pelo Teorema 2 um grafo de vértices tem de ter:
Como , conclui-se que não é planar
AVISO
Um grafo pode respeitar as condições do Teorema 2 e não ser planar. Só podemos tirar conclusões se não respeitar a igualdade.
Teorema 3
Num grafo conexo planar de vértices, que não tem triângulos, tem-se
Exemplo
Um grafo bipartido com partições de dimensão não é planar.
A região mínima é um quadrado.
Se verificarmos, temos arestas. Pelo Teorema 3 temos de ter no máximo em grafos com vértices.
não é planar.
Teorema 4
Num grafo planar há sempre pelo menos um vértice de grau .
Demonstração
Imagine-se que afinal havia pelo menos um vértice de grau .
Então, para grafos onde os vértices têm todos grau , pelo Teorema Fundamental da Teoria dos Grafos
Onde é o número de vértices e o número de arestas.
O que significa que não pode ser planar pelo Teorema 2.
QED