Labirintos
Definições
Atalhos Eulerianos
Atalhos que percorrem todos os vértices e arestas.
Relembrar que um atalho nunca repete arestas.
Os Atalhos Eulerianos também podem ser fechados (se acabarem no mesmo vértice) ou abertos (se não acabarem no mesmo vértice).
Um atalho euleriano fechado também se pode designar por circuito euleriano e um atalho euleriano aberto por travessia euleriana.
Multigrafo Euleriano
Um multigrafo euleriano é um multigrafo que tem um atalho euleriano fechado.
Multigrafo Atravessável
Um multigrafo atravessável é um multigrafo que tem um atalho euleriano aberto.
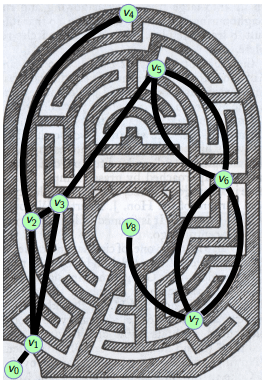
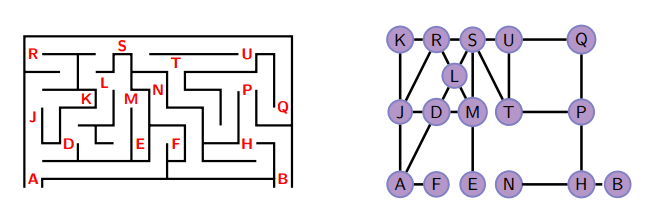
Representar um Labirinto com Grafo
Seja uma encruzilhada um sítio no labirinto, onde se pode escolher vários caminhos.
Podemos representar um Labirinto através de um grafo, onde todas as entradas, saídas, centros, encruzilhadas e becos sem saída do labirinto são vértices e as arestas são os caminhos que existem entre cada vértice.
Teoremas e Algoritmos
Teorema de Euler-Hierholzer
Um multigrafo é euleriano se e só se é conexo e todo o seu vértice é par.
Relembrar: Conexo significa que quaisquer dois vértices estão conectados (não há vértices isolados).
AVISO
No próximo teste haverá uma Demonstração, segundo o professor, que também disse que a Demonstração seguinte é Muito Importante. Se esta não ficar clara, poderá ficar mais fácil assistir à Prova feita pelo professor em aula, uma vez que são usados vários desenhos explicativos. Esta pode ser encontrada aqui e começa em 47:10 e acaba em 1:04:20.
Demonstração
- Condição Necessária
Seja um multigrafo euleriano, então este terá um atalho euleriano fechado (passa por todos os vértices e arestas, sem repetir arestas e acabando no vértice por onde começamos). Aqui podemos concluir logo que é conexo.
Supondo que começávamos o atalho num vértice , então, para todo o vértice do multigrafo diferente de , vamos ter de, obrigatoriamente, "chegar" e depois "sair" do vértice, visto que temos de percorrer todos os vértices e não podemos terminar o atalho sem ser em .
Quando saímos (e entramos) num vértice, nunca pode ser por uma aresta já percorrida, porque o multigrafo é euleriano. Deste modo, é fácil reparar que todo o vértice diferente de terá grau par, porque saímos e entramos sempre por arestas diferentes (não importa quantas vezes).
Já se provou que todo o vértice diferente de (vértice inicial) é par, agora falta provar o mesmo para .
A única diferença, face aos restantes vértices, é que em saímos primeiro. Tal como nos outros vértices, também podemos entrar e sair de , durante o atalho. Contudo, o seu grau também será par, porque no final regressamos a , por uma aresta diferente.
- Condição Suficiente - A parte mais Importante, segundo o professor
Seja um multigrafo conexo e com todos vértices são pares. Vamos tentar provar que é um multigrafo euleriano, por absurdo.
Sendo o maior atalho fechado que podemos arranjar em onde não é um atalho euleriano fechado. Deste modo, há arestas que não foram percorridas em .
Seja o grafo, que resulta de eliminar todas as arestas de . Se não era um atalho euleriano fechado, então tem de ter arestas.
Como é um atalho fechado, vamos remover a cada vértice um número par de arestas, então em vamos continuar com os vértices todos pares (relembrar que tinha os vértices todos pares).
Como era conexo, existe um vértice de onde passava o atalho , que não é isolado (relembrar que tem arestas). Esse vértice terá grau par .
Uma vez que os vértices têm todos grau par, será sempre possível "entrar" e "sair" de um vértice e se começarmos por sair de um, vamos, obrigatoriamente, ter de regressar ao mesmo, algures no atalho. Então existirá um atalho fechado a começar e acabar em , que vamos designar por
Finalmente, se existe um atalho fechado a começar e acabar em , com arestas não pertencentes a , será possível juntar os dois atalhos num só. Repare-se que, se é um atalho fechado, então podemos fazer um atalho semelhante, só que acaba e começa em , mas, em vez de terminarmos, passamos a percorrer o atalho , acabando finalmente em .
Chegamos a um absurdo, afinal não é o maior atalho fechado que podemos arranjar em se não for um atalho euleriano fechado.
QED
NOTA
É importante referir também que este processo é recursivo. Poderíamos voltar a considerar um novo grafo, mas que a agora seria o resultado de retirar o atalho "" e chegaríamos à mesma conclusão. Só terminará se for um grafo de vértices isolados (sem arestas) e nesse caso conclui-se que o atalho fechado era um atalho euleriano fechado.
Teorema 2
Um multigrafo é atravessável se e só se tem apenas dois vértices ímpares.
Para além disso, o atalho Euleriano aberto começa e acaba nos vértices ímpares, onde o primeiro é diferente do último.
AVISO
Demonstração semelhante à anterior. Também é Muito Importante, segundo o professor e na aula o professor usou desenhos explicativos que podem ajudar a perceber.
Podem encontrar a aula no mesmo link começa em 1:06:50 e acaba em 1:20:00.
Demonstração
-
Condição Necessária
Seja um multigrafo atravessável, significa que, se eu partir de um vértice , consigo percorrer um
atalho euleriano aberto(travessia euleriana), ou seja, que percorre todas as arestas sem repetições e termina num vértice diferente, .Supondo que agora criávamos uma nova aresta de a , de modo a que fosse possível percorrer um
circuito euleriano(atalho euleriano fechado). Basta pensar natravessia eulerianaque tinhamos e agora acrescenta-se uma aresta que liga a .
NOTA: e poderiam até já ter arestas que os interligassem, mas não eram suficientes para formar umcircuito euleriano.Como se sabe, um
circuito eulerianotem todos os vértices pares. Então, se removermos a aresta que adicionámos e passaram a ter grau ímpar e serão os únicos, pois a aresta removida era comum aos dois. Os outros vértice permanecerão com grau par.Logo, se é atravessável , então tem pelo apenas vértices com grau ímpar.
-
Condição Suficiente
(A ideia é quase igual à da Condição Necessária)
Seja um multigrafo com apenas vértices com grau ímpar.
Se unitrmos esses vértices com uma nova aresta, pelo Teorema de Euler-Hierholzer terá um
circuito euleriano.
Então, se eu remover a aresta adicionada, passará a ter umatravessia euleriana, logo será atravessável.
QED
NOTA
A prova para grafos (não multigrafos) é muito parecida. A única diferença é que temos de adicionar um vértice com duas arestas, uma que se liga a outra a , porque podemos ter uma travessia como:
Como estamos a trabalhar com grafos, não podemos ter mais do que aresta a ligar vértices.
Apesar desta exceção a prova é igual, só que retiramos/adicionamos arestas e vértice como descrito.
Teorema 3 - Teorema de Euler
Se tivermos um grafo que não seja Euleriano, podemos duplicar cada aresta e dessa maneira todos os vértices terão grau par, assim já é Euleriano.
NOTA: Outra solução é percorrer cada aresta duas vezes, em vez de duplicar.
Teorema 4 - Teorema de Lucas
Um multigrafo conexo com vértices ímpares pode ser descrito por exatamente atalhos abertos que não partilham arestas.
Algoritmo de Fleury
Com este Algoritmo consegue-se percorrer um atalho euleriano fechado num multigrafo euleriano.
- Começa-se num vértice qualquer
- Se houver mais que aresta possível a percorrer, escolhe-se uma que não seja
Ponte(não interessa qual, desde que não seja umaPonte) - Só se atravessam as
Pontesem último caso (quando já não há mais arestas disponíveis).
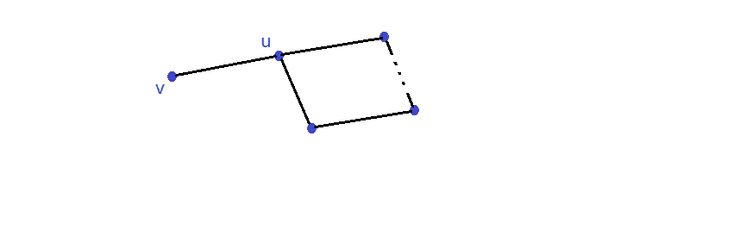
Relembrar: Ponte é uma aresta que, se removida, cria uma nova componente.
Exemplo
O exemplo encontra-se neste link
Algoritmo Fleury - Multigrafo Atravessável
O Algoritmo de Fleury foi concebido para multigrados eulerianos.
Mas, também o podemos aplicar, informalmente, em multigrafos atravessáveis.
Para isso, basta começar num vértice ímpar, é a única mudança no Algoritmo. Mas, neste caso, não vamos acabar no mesmo vértice, mas sim no outro vértice ímpar.
Reparem que, se, num multigrafo atravessável, ligarmos os dois vértices ímpares com uma aresta, ficamos com um multigrafo euleriano. Nesse caso, já poderíamos acabar no vértice inicial.
Desvantagens
Não funciona em Labirintos se não o conhecermos, uma vez que nesses caso não sabemos se um aresta (caminho do Labirinto) é Ponte ou não.
Algoritmo de Trémaux
Com as regras deste Algoritmo, qualquer um pode sair de qualquer labirinto.
Passamos agora à descrição do Algoritmo:
- Sempre que chegamos a um vértice não visitado anteriormente, seguimos por uma aresta também não percorrida, qualquer.
- Sempre que chegarmos a um vértice através de uma aresta ainda não percorrida anteriormente, se chegarmos a um vértice já visitado ou a um beco sem saída, voltamos para o vértice de onde viemos pela aresta.
- Sempre que chegarmos a um vértice através de uma aresta que já tinha sido percorrida anteriormente e chegarmos a um vértice já visitado, escolhemos a aresta ainda não percorrida que incide no vértice. Se não existir, escolhemos percorrer uma aresta que já tenha sido percorrida apenas uma vez.
Exemplo
O exemplo encontra-se neste link
Algoritmo de Tarry
Se chegarmos a um vértice, escolhemos continuar por qualquer aresta que não tenha sido percorrida vezes (dando prioridade às arestas ainda não percorridas), com exceção da aresta onde chegamos pela primeira vez ao vértice atual.
Só percorremos essa aresta em último caso, ou seja, se for um beco sem saída, ou se as outras arestas já tiverem sido percorridas vezes.
Exemplo
O exemplo encontra-se neste link.
Teorema de Tarry
Iniciando um caminho num grafo conexo qualquer, e seguindo as regras do Algoritmo de Tarry, regressaremos ao vértice inicial, depois de ter percorrido cada aresta do grafo vezes em sentidos opostos.