Algoritmos de Gale-Shapley
Definições
Grafo k-partido
Um grafo diz-se -partido se existe uma partição do conjunto dos seus vértices em conjuntos, nenhum deles contendo vértices adjacentes.
Se pode-se chamar bipartido, se tripartido e para multipartido.
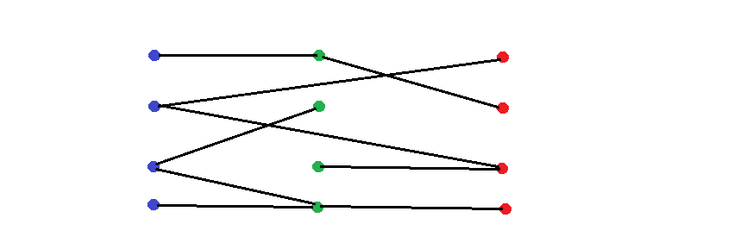
Exemplo
É um grafo tripartido. Repare-se que existe uma partição em conjuntos (azuis, verdes e vermelhos), e em cada conjunto não há vértices adjacentes.
Algoritmo da Estabilidade
Relacionamento
Sejam e dois conjuntos finitos equipolentes (com o mesmo tamanho), que representam o conjunto de Rapazes e Raparigas, respetivamente. Seja uma bijeção, representa um relacionamento entre rapazes e raparigas que consiste numa lista de pares , designada Lista de Relacionamentos.
Como é uma bijeção, também podemos ter a relação inversa .
Bloqueio
Usando o exemplo do Relacionamento entre Rapazes e Raparigas, diz-se que o par , , é um Bloqueio na lista de relacionamentos, se não pertence à lista de relacionamentos, mas preferia estar com do que com e preferia estar com do que com .
Uma Lista de Relacionamentos diz-se Estável se não existirem pares de bloqueio em .
Lista de Preferências
Usando mais uma vez o exemplo do Relacionamento entre Rapazes e Raparigas, cada Rapaz e cada Rapariga poderá ter uma Lista de Preferências onde apresenta os membros do conjunto oposto que prefere por ordem.
Exemplo
Neste exemplo vamos trabalhar com o Relacionamento entre Rapazes e Raparigas, onde temos Raparigas e Rapazes.
A seguinte tabela é um exemplo de Lista de Preferências
Exemplo de Lista de Relacionamentos Estável:
Exemplos de Listas de Relacionamentos Instáveis:
-
Esta lista tem umBloqueio. Repare-se que o Rapaz prefere a Rapariga à Rapariga (o seu par na lista) e a Rapariga prefere o Rapaz ao Rapaz (o seu par na lista). -
Esta lista temBloqueios:
Algoritmo da Estabilidade
Serve para verificar se uma Lista de Relacionamentos é estável ou instável.
O Algoritmo é descrito pelo seguinte pseudo-código.
Algoritmo de Gale-Shapley
Descrição Do Algoritmo
Informal
- Cada Rapaz e Rapariga ou estão comprometidos ou livres
- Cada Rapariga, assim que fica comprometida, continuará nesse estado durante o resto da execução do algoritmo. Poderá, eventualmente, trocar de par
- Todo o Rapaz que pede em namoro mais do que uma vez, fica com namoradas cada vez menos desejáveis
- As Raparigas ficam tanto mais favorecidas quanto maior for o número de trocas de namorado
- Quando um Rapariga livre recebe uma proposta, aceita e fica comprometida
- Quando uma Rapariga comprometida recebe nova proposta, compara o novo pretende com o namorado e escolhe ficar com o que lhe favorece mais
- Cada Rapaz pede namora às Raparigas seguindo a sua ordem de preferência
- Assim que um Rapaz é rejeitado, propõe-se imediatamente à Rapariga seguinte na sua Lista de Preferências.
Pseudo-Código
NOTA
Não importa qual a ordem das propostas dos Rapazes, o Algoritmo acabará sempre na mesma Lista
Correção Do Algoritmo de Gale-Shapley
Para toda a instância do problema do relacionamento estável, o algoritmo Gale-Shapley termina com uma lista de relacionamentos estáveis.
Demonstração
- Provar que cada Rapaz está associado a uma Rapariga
Como cada Rapariga aceita sempre uma proposta se estiver livre, se um Rapaz pedir namoro à última rapariga da sua Lista de Preferências, significa que as outras Raparigas têm par (namorado), a última só o rejeitará se também tiver namorado.
Isso é impossível, pois só se confirmaria se o número de Rapazes fosse maior que o número de Raparigas, o que nunca se verifica.
Se um Rapaz chegar à última Rapariga ela aceita-o sempre.
- Provar que o algoritmo termina.
Como nenhum rapaz se pode propor vezes à mesma Rapariga, o número máximo de propostas que poderá haver são , onde . Como é um número finito, o Algoritmo tem fim.
- Provar que no final a Lista é Estável
Se o Rapaz acabou por não ficar relacionado com uma rapariga , que preferia em relação à com quem ficou , então é porque o rejeitou.
Se o rejeitou foi porque tinha recebido uma proposta de um pretendente que preferia, não havendo assim Bloqueio.
Deste modo, será impossível encontrar Bloqueios na Lista final que resulta de aplicar o Algoritmo.
QED
Exemplos da Emulação do Algoritmo
No teste só poderemos usar Maneiras, ambas exemplificadas abaixo.
Maneira 1
Resolução:
- Rapaz propõe-se à Rapariga ; ela aceita
- Rapaz propõe-se à Rapariga ; ela rejeita
- Rapaz propõe-se à Rapariga ; ela aceita e rejeita o Rapaz
- Rapaz propõe-se à Rapariga ; ela aceita e rejeita o Rapaz
- Rapaz propõe-se à Rapariga ; ela aceita
- Rapaz propõe-se à Rapariga ; ela aceita e rejeita o Rapaz
- Rapaz propõe-se à Rapariga ; ela aceita
- Rapaz propõe-se à Rapariga ; ela aceita
A Lista de Relacionamentos obtida é que é estável.
Maneira 2
Resolução:
Consequências
Teorema 1
Todas as possíveis execuções do algoritmo de Gale-Shapley (tendo os rapazes como proponentes *) produzem o mesmo relacionamento estável, e, neste relacionamento estável, cada rapaz obtém a melhor das parceiras que pode ter em qualquer relacionamento estável.
* são os Rapazes que se propõem às raparigas, como descrito inicialmente no Algoritmo. Se fossem as Raparigas as proponentes, os papeis invertiam-se.
Demonstração
Sendo um parceiro estável de , um par com numa dada Lista Estável.
Supondo que uma certa execução do Algoritmo de Gale-Shapley produz um Relacionamento estável que inclui o par .
Imaginemos que não é o Relacionamento estável que mais beneficia , porque existe outro Relacionamento estável , onde está relacionado com , que prefere a .
Pelo Algoritmo, conclui-se que, numa dada iteração de , teve de rejeitar (Relembrar que os Rapazes vão se propondo às Raparigas segundo a sua preferência).
Supondo que essa rejeição (de face a ), foi a primeira vez em que uma rapariga rejeito um parceiro estável, pois preferia outro Rapaz a .
Se nenhuma rapariga rejeitara um parceiro estável antes, então não tem nenhuma parceira estável que prefira a .
Então, como em temos o par e está relacionado com uma Rapariga que não prefere, em relação a , é óbvio que o par é um bloqueio de . Assim, este Relacionamento não é estável.
Conclui-se que, qualquer Relacionamento, onde um Rapaz fica com uma Rapariga que prefere em relação ao seu par que resultou da Aplicação do Algoritmo de Gale-Shapley, é Instável.
QED
Teorema 2
No relacionamento estável optimal para os rapazes, cada rapariga obtém o pior parceiro que pode obter em qualquer relacionamento estável.
NOTA
Relacionamento Estável Otimal para Rapazes/Raparigas:
Relacionamento Estável, onde os Rapazes/Raparigas obtêm o melhor parceiro possível.
Demonstração
Tentando provar por absurdo.
Vamos supor que o Teorema é Falso e que, sendo o relacionamento estável otimal para os Rapazes, que resulta do Algoritmo de Gale-Shapley, existe outro relacionamento estável , onde uma dada Rapariga fica com um rapaz , que prefere menos em relação ao rapaz com que ficou em .
Como é otimal para os Rapazes , em ficará com uma rapariga que prefere menos, em relação a . Para além disso, também ficou com um Rapaz que prefere menos em relação ao .
Conclui-se que é um Bloqueio de , logo não é estável.
QED