Teoria do Fluxo

Definições

Digrafo

Grafo dirigido, todas as arestas têm orientação.

Exemplo

Grau de Entrada/Saída

Seja $v$ um vértice de um digrafo $d$:

• Grau de Entrada: Quantas arestas estão direcionadas para $v$
• Grau de Saída: Quantas arestas partem de $v$ para outro vértice

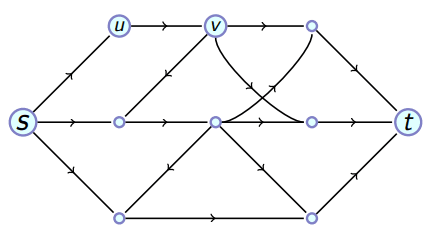
Exemplo

Neste exemplo, o vértice v tem

• Grau de entrada $1$
• Grau de saída $3$

O vértice S tem

• Grau de entrada $0$
• Grau de saída $3$

Fonte e Sumidouro

Fonte é o vértice de um digrafo conexo com grau de entrada nulo.
Sumidouro é o vértice de um digrafo conexo com grau de saída nulo.

Rede Capacitada

Uma rede capacitada $N=(V,E,s,t,\operatorname{cap})$ é um digrafo-$s$-$t$ $(V,E,s,t)$, com uma função capacidade $\operatorname{cap}: V \times V \rightarrow \N$, tal que, para vértices $v_i, v_k \in V$:

• $\operatorname{cap}(xy)=0$ se $xy \notin E$ (não é aresta do digrafo)
• $\operatorname{cap}(xy)\geq0$ se $xy \in E$

Fluxo

Um Fluxo numa Rede Capacitada $N=(V,E,s,t,\operatorname{cap})$ é uma atribuição de valores $\operatorname{f}: V \times V \rightarrow \N$ às arestas do digrafo-$s$-$t$ $(V,E,s,t)$, onde:

• $\operatorname{f}(xy)=0$ se $xy \notin E$
• $\operatorname{f}(xy)\geq0$ se $xy \in E$
• $\operatorname{f}(xy) \leq \operatorname{cap}(xy)$ (Fluxo não pode exceder capacidade)
• Fluxo que entra num vértice $v$ é igual ao fluxo que sai de $v$

Valor do Fluxo

O Valor de um Fluxo numa Rede Capacitada será igual ao somatório do fluxo que sai da Fonte, ou Fontes se houver mais do que uma.

Dica

Podemos ver uma Rede Capacitada, como uma rede de canalização da água, onde há uma fonte, destino(sumidouro) e as arestas são canos de água. Tal como na Rede Capacitada, um cano não tem água a circular nos dois sentidos, apenas num.
Seguindo esta ideia,

• Capacidade $(\operatorname{cap})$ indica a quantidade máxima de água que cada cano aguenta.
• Fluxo $(\operatorname{f})$ indica a quantidade de água que está a passar em cada um dos canos
• O Valor do Fluxo é quantidade de água que emitimos na fonte.

Fluxo Máximo

Fluxo máximo é um fluxo $\operatorname{f}$, tal que o seu valor é maior ou igual ao valor de qualquer outro fluxo possível na mesma Rede capacitada.

Corte

Numa Rede $N=(V,E,s,t,\operatorname{cap})$, sejam $V_s$ e $V_t$ uma partição de $V$ $(V_s\cap V_t = \emptyset \quad \wedge \quad V_s\cup V_t =V)$, tal que $s \in V_s$ e $t \in V_t$.
Ao conjunto de arestas orientadas de vértices em $V_s$ para vértices em $V_t$, ou dá-se o nome de Corte na rede $N$ e denota-se por $(V_s,V_t)$

Capacidade do Corte

Soma das capacidades de todas as arestas do corte.

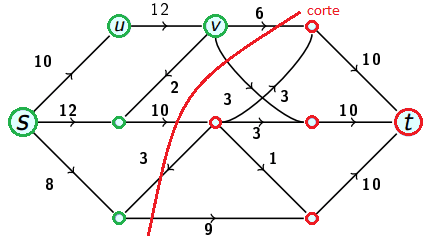
Exemplo

Neste Corte a vermelho a capacidade do Corte será:

$$6+3+10+9 = 28$$

Nota

A aresta com capacidade $3$ mais abaixo não é incluída, porque vai de $V_t$ para $V_s$

Balanço de Fluxo

Balanço de fluxo, através de um corte $C = (V_s,V_t)$, que também pode ser identificado por Fluxo do Corte $C$, é a soma dos fluxo das arestas orientadas de $V_s$ para $V_t$ (fluxo positivo) menos a soma dos fluxos das arestas orientadas de um vértice de $V_t$ para $V_s$ (fluxo negativo).
Qualquer Corte numa Rede Capacitada tem sempre o mesmo Balanço de Fluxo.

Exemplos

O Balanço do Fluxo deste corte será:

$$6+3+10+9 - 3=25$$

Corte mínimo

Corte, cuja capacidade é menor ou igual à capacidade de qualquer outro corte da mesma Rede.

Trajetória num Digrafo

Uma trajetória numa rede capacitada $N=(V,E,s,t,\operatorname{cap})$ é uma trajetória aberta de $s$ a $t$.

Relembrar dos Grafos: Trajetória aberta é um caminho que não repete vértices nem arestas, e que não é fechada (não acaba no mesmo vértice)

Quasi-trajetória

Trajetória, mas que pode ter arestas negativas. Seja

uma Quasi-trajetória, pode existir uma aresta $a_i$ (*com $1<i<k$) que está dirigida de $v_i$ para $v_{i-1}$. Este tipo de arestas é designado por arestas negativas

Exemplos

Ambas representam Quasi-Trajetórias, mesmo que a vermelha não tenho arestas negativas

Frouxidão

Seja $Q$ uma Quasi-Trajetória e $a$ uma aresta que faz parte de $Q$, a Frouxidão de $a$ é dada por:

(Obrigado ao Rafael Oliveira)

A Frouxidão mínima de uma Quasi-trajetória $(\Delta_Q)$ será a mínima frouxidão de entre todas as arestas de $Q$.

Incremento do Fluxo

Seja $Q$ uma Quasi-Trajetória, é possível incrementar o seu fluxo, se a Frouxidão mínima for maior que $0$.

Nesse caso, seja $(\Delta_Q)$ a frouxidão mínima de $Q$, adicionamos $(\Delta_Q)$ ao fluxo das arestas positivas, e retiramos $(\Delta_Q)$ do fluxo das arestas negativas

Teoremas

Teorema 1

O valor de um fluxo é menor ou igual à capacidade de um corte mínimo numa rede capacitada.
Se o valor do fluxo $\operatorname{f}$ é igual à capacidade de um corte $(V_s,V_t)$, então o fluxo $\operatorname{f}$ é máximo e o corte $(V_s,V_t)$ é um corte mínimo.

Demonstração

Seja $\operatorname{f_c}$ o fluxo de um corte $C = (V_s,V_t)$.
Se $\operatorname{f_c}$ é igual à capacidade do corte, então, pela fórmula do fluxo de um corte, a soma dos fluxos das arestas orientadas de um vértice de $V_t$ para $V_s$ (fluxo negativo) será $0$.

Deste modo, o fluxo será máximo, porque é igual à capacidade, e por isso, o corte também será mínimo

QED

Teorema 2

Um fluxo $\operatorname{f}$ numa Rede Capacitada $N$ é um fluxo máximo se e só se não existir uma Quasi-trajetória de incremento do fluxo.

Demonstração

Condição Necessária - Se não existe Quasi-Trajetória de aumento, o fluxo é máximo.

Vamos definir um corte $(V_s,V_t)$ mínimo:

1. $s \in V_s$ (relembrar que $s$ é a fonte)
2. Se $u \in V_s$ e $\operatorname{f}(uv)<\operatorname{cap}(uv)$, então $v \in V_s$
3. Se $u \in V_s$ e $\operatorname{f}(vu)>0$, então $v \in V_s$
4. $V_t = V - V_s$

Face a estas restrições, $t$ (o sumidouro) terá de pertencer a $V_t$, pois, se não pertencesse haveria uma Quasi-Trajetória de aumento, que não existe como assumido no início da Condição Necessária.
Logo, $(V_s,V_t)$ é um corte.

O fluxo será máximo se for igual à capacidade do corte.
Seja $a_1$ uma aresta do corte $(V_s,V_t)$, esta aresta tem de estar saturada, caso contrário ambos os vértices das arestas pertenceriam a $V_s$ (ponto $2$)
Seja $a_2$ uma aresta que vai de $V_t$ para $V_s$, terá fluxo $0$ (ponto $3$).

Aplicando o Teorema 1, o Teorema 2 fica demonstrado

QED

Aviso do Professor

Isto só se verifica numa Rede Capacitada com números Racionais. Há situações com números Reais onde não podemos concluir nada.
Contudo, esta exceção não deve ser avaliada.

Algoritmo de Ford-Fulkerson

Numa Rede capacitada $N=(V,E,s,t,\operatorname{cap})$, permite-nos encontrar o Fluxo máximo e, consequentemente, o Corte mínimo.

Pseudo-Código

Descrição Informal

Sempre que houver uma Quasi-Trajetória $Q$ com Frouxidão mínima positiva, aumentamos o fluxo de $Q$.
Quando já não houver termina o algoritmo (pelo Teorema 2), e teremos uma Rede Capacitada com Fluxo máximo.

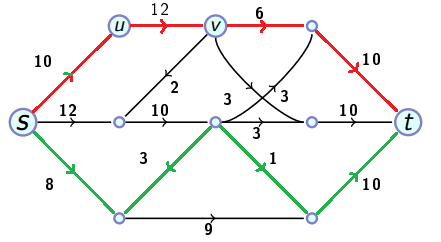
Corte mínimo pelo Ford-Fulkerson

Seja $V_s$ o conjunto dos vértices alcançáveis no final do Algoritmo de Ford-Fulkerson e $V_t$ tal que $V_s\cap V_t = \emptyset \quad \wedge \quad V_s\cup V_t =\{\text{conjunto de todos os vértices}\}$, $(V_s,V_t)$ é um Corte Mínimo, porque respeita as condições do Teorema 1.

Vértice alcançável

Um vértice $v$ é alcançável se é possível aumentar o fluxo de uma "pseudo" Quasi-trajetória que começa na fonte e vai até ao vértice $v$.

Exemplo do Ford-Fulkerson + Corte

Link