Funções Geradoras
Definição
Tome-se o número de maneiras que se pode fazer x euros com moedas de 1 euro:
1z0+1z1+1z2+1z3+…1zx
Onde o coeficiente de zx representa o número de formas possíveis de distribuir as moedas.
Assim, o número de maneiras que se pode fazer x euros com moedas de 2 euros é:
1z0+0z1+1z2+0z3+⋯+0z2x−1+1z2x
Abaixo está como averiguar o número de formas possíveis de obter 8 euros com moedas de 1 euro e de dois.
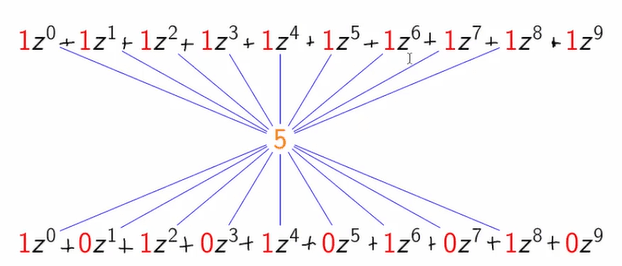
ou, de modo geral:
cn=k=0∑nakbn−k
Generalização e Exemplos
Em geral, uma sucessão un é gerada por:
un⟶v(z)=k=0∑+∞ukzk
seja un=1,1,1,1,1,1,0,0,…:
v(z)=1+z+z2+z3+z4+z5 ouv(z)=1−z1−z6=z−1z6−1
ou então un=1,3,3,1,0,0,…:
v(x)=1+3z+3z2+z3=(1+z)3
ou então un=1∀n∈N:
v(z)=1+z+z2+z3+z4+…z⋅v(z)=z+z2+z3+z4+⋯⇔v(z)−z⋅v(z)=1⇔v(z)=1−z1
Com estes exemplos, já podemos conhecer a função geradora de un=n+1
:
v(z)=1z0+2z1+3z2+4z3+…z⋅v(z)=z+2z2+3z3+4z4+…(1−z)v(z)=1+z+z2+z3+z4+⋯=1−z1⇔v(z)=(1−z)21
Repare-se que a partir desta fórmula pode-se também chegar a geradora de un=n:
un=n+1⟹v(z)n+1=k=0∑+∞(k+1)zk=k=0∑+∞kzk+k=0∑+∞zk
onde o primeiro somatório da última igualdade representa a geradora da sucessão un=n. Assim, viria:
v(z)n=(1−z)2z
Agora, para un=3n:
v(z)=k=0∑+∞3kzk=k=0∑+∞(3z)k=(1−w1)w=3z=1−3z1
Ou, de um modo geral:
un=an⟹v(z)un=1−az1
Já agora, a função geradora para as moedas de dois euros seria:
D(z)=k=0∑+∞(z2)k=1−z21
Voltando agora ao exemplo inicial, vamos ver quantas formas há de obter x euros a partir de moedas de 1 e 2 euros:
G(z)=v(z)D(z)=(1−z)(1−z2)1=(1−z)2(1−(−z))1
Agora, tem-se:
(1−z)2(1−(−z))1=1−z41+(1−z)221+1−(−z)41
agora, relacionando com as fórmulas já vistas:
(1−z)2(1−(−z))1=41×1+41(n+1)+41×(−1)n 42n+3+(−1)n
Exemplo, há 42(6)+3+(−1)6=4 formas possíveis de formar 6 euros a partir de moedas de 1 e 2 euros.
