Grafos - Início
O que é um Grafo?
Um grafo é um par , onde:
- é um conjunto de vértices finito e não vazio
- é o conjunto dos dos pares de vértices que estão ligados por uma aresta
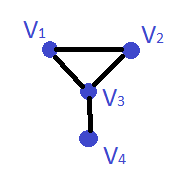
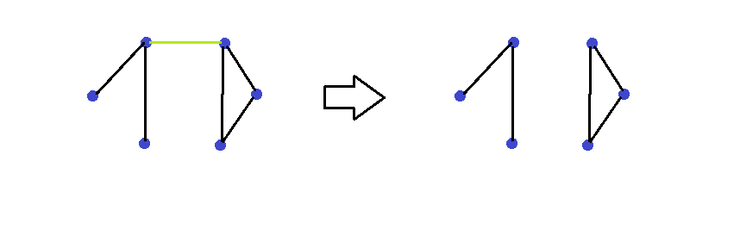
Por exemplo
Como uma aresta não tem direção, em representa-se os dois pares das "direções" de cada aresta.
Contudo, como isto é uma propriedade conhecida dos grafos, também se pode represente um grafo por , onde é o conjunto sem repetições.
No caso do exemplo acima, um possível seria
Definições e Teoremas
Ordem e Tamanho do grafo
Ordem do grafo, , é o número de vértices do grafo.Tamanho do grafo, , é o número de arestas do grafo
Seja ,
Relembrar
= número de elementos do conjunto
Grau de um vértice
. Para um vértice , o seu grau em corresponde ao número de arestas de que incidem em .
Representa-se por:
Teorema Fundamental da Teoria dos Grafos
Num grafo , a soma dos graus dos seus vértices é igual ao dobro do Tamanho do grafo.
Demonstração
Primeiro define-se a seguinte operação
Seja um vértice e uma aresta de ,
número de vezes que a aresta incide em
Seja a soma dos graus dos vértices de ,
QED
é 2, pois cada aresta está associada a 2 vértices.
Teorema 2
Num grafo , o número dos seus vértices ímpares é par.
NOTA
vértice é par/ímpar tem grau par/ímpar.
Demonstração
Para , onde
Pelo Teorema Fundamental da Teoria dos Grafos, a soma dos graus é , com o número de arestas.
Assim sendo, será um número par. Como a soma dos graus dos vértices pares é par, para o resultado final também ser par, é obrigatório haver um número par de vértices ímpares.
QED
Aplicações
Exercício 5 da Série 4
Um certa comissão parlamentar da Assembleia da República é composta por 15 deputados. Conclua que
não é possível que cada um deles já tenha estado em comissões parlamentares anteriores com exatamente 5
dos outros deputados que fazem parte desta comissão.
Se se desenhar um grafo onde os vértices são os deputados e as arestas ligam dois deputados que tenham estado juntos em comissões anteriores, o grafo teria um número ímpar de vértices com grau ímpar , o que pelo Teorema 2 é impossível.
QED
Grafo Regular
Um grafo diz-se regular se todos os seus vértices têm o mesmo grau.
Um grafo diz-se -regular se os seus vértices têm grau .
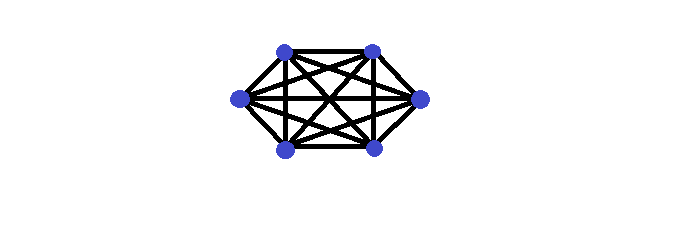
Grafo Completo
Um grafo diz-se completo quando cada par de vértices constitui uma aresta (está tudo ligado).
NOTA
- Todo o grafo completo de vértices é -1 regular
- é o número máximo de arestas que um grafo pode ter
- grafo completo de vértices
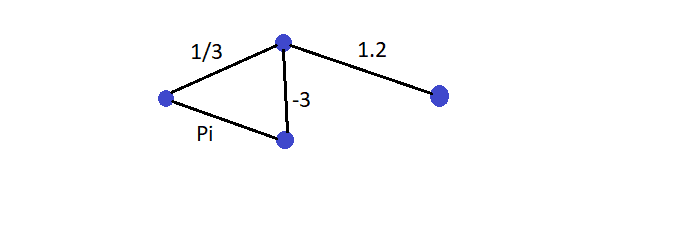
Rede
É um terno , onde é um grafo subjacente à Rede e uma aplicação (todos os elementos de têm correspondência).
Em suma, uma Rede é um grafo onde as arestas têm valores reais associados.
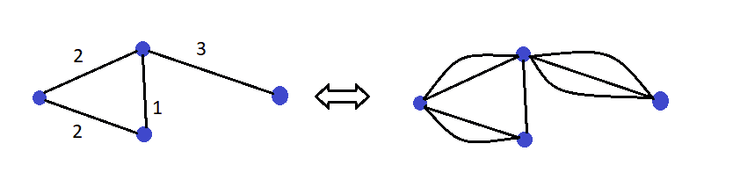
Multigrafo
É uma Rede onde as arestas estão associadas a valores naturais. Pode-se representar um multigrafo substituindo cada aresta por arestas, onde é o valor associado. (Com o exemplo fica claro)
NOTA
É normal referir-se a multigrafos como apenas grafos. O novo termo é só usado para evitar ambiguidade quando temos grafos e multigrafos.
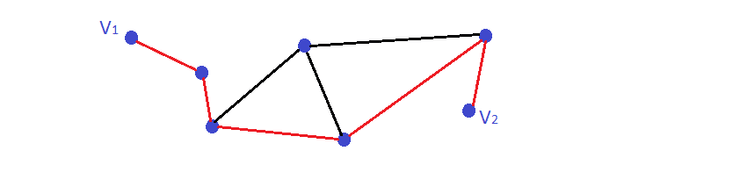
Caminho
Num grafo é uma sequência alternada de vértices e arestas , onde , , ou seja, cada aresta liga os vértices ao seu lado.
Atalho
Caminho que não repete arestas.
Trajetória
Caminho que não repete vértices, exceto no caso dos vértices inicial e final coincidirem. Neste caso a Trajetória é fechada, caso contrário é aberta.
Vértices Conectados
Dois vértices e de um grafo dizem-se conectados se forem o mesmo vértice ou se existir um caminho onde as extremidades são e
Grafo Conexo
Um grafo é conexo se quaisquer dois vértices do grafo estão conectados.
Subgrafo
Dado um grafo , diz-se que o grafo é subgrafo de se ou .
Um grafo é subgrafo de si mesmo
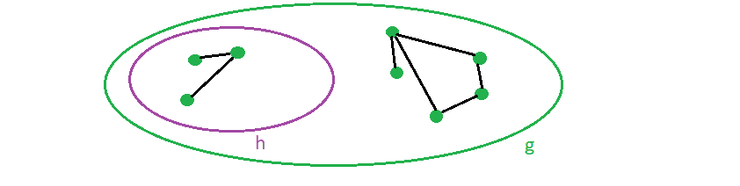
Componente
é uma componente de um grafo , se for um subgrafo conexo de e não for subgrafo de nenhum outro subgrafo conexo de .
Grafo Planar
Grafo que é possível desenhar sem cruzar arestas.
Teorema 3 - Lei de Euler
Seja um Grafo Planar, existe a seguinte relação:
NOTA
A Região "Exterior" também conta
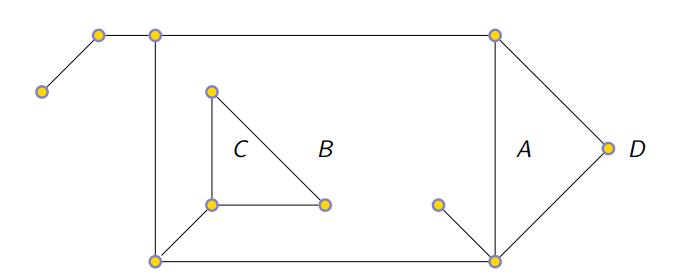
Ponte
Aresta de um grafo, que, se for removida, aumenta o número de componentes.
Teorema 4
Num grafo de vértices e componentes, o nº de arestas é tal que:
Demonstração
- Provar que
Por indução simples, variando o Tamanho do Grafo
,
Neste caso o número de vértices é igual ao número de componentes.
Hipótese: Grafos com arestas (não importando o nº de componentes e vértices): .
Para esta prova, vamos supor que o grafo é esquelético, ou seja, todas as arestas são pontes. (No final da Demonstração há um exemplo de grafo esquelético.)
Se a prova funcionar para grafos esqueléticos funcionará para qualquer um, pois estes têm o menor número de arestas para um dado número de vértices.
Se removermos uma aresta de um grafo esquelético, o número de componentes aumenta.
Deste modo, por hipótese de indução
O que é válido, pois .
A primeira inequação está provada .
- Provar que
Como estamos a tentar provar que o número de arestas tem um limite máximo, vamos ter em conta sempre os casos "máximos".
Seja uma componente do grafo em estudo. Se essa componente tem vértices, tem no máximo arestas.
Se o grafo tem componentes, o que acontecerá se transferirmos um vértices de uma componente para outra?
Seja e duas componentes com e , respetivamente e (o que é verdade para quaisquer duas componentes, haverá com mais vértices, ou têm as duas o mesmo número).
Seja a variação do número de arestas nas componentes e , quando "transferimos" um vértice de para .
A variação total será e será positiva pois
Assim, com o que acabamos de verificar, podemos concluir que um grafo com componentes terá o números máximo de arestas se e só se tem:
- vértices isolados
- componente com vértices
Nestas condições, o número máximo de arestas será:
Finalmente, podemos concluir que
A segunda inequação está provada .
QED
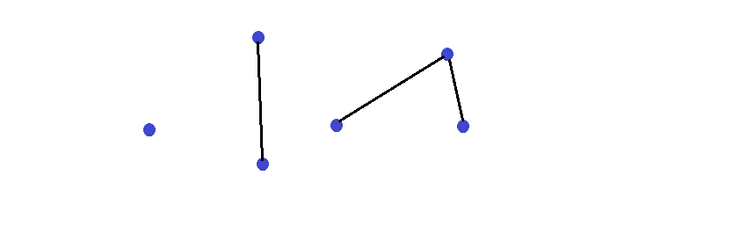
Exemplo Grafo Esquelético
Teorema 5
Se um grafo de vértices tem mais de arestas, então é conexo.
Demonstração
Se o grafo não for convexo tem pelo menos componentes. Seja o número de arestas, pelo Teorema Anterior
Logo, como também vimos no Teorema Anterior que a "transferência" de vértices entre componentes aumenta , se passarmos todos os vértices de uma componente para outra (passando agora a ter apenas ), conclui-se que será maior do que a expressão acima.
QED