Algoritmos Elementares de Ordenação

Características de Algoritmos

Bem, vamos contactar com algoritmos de ordenação, sejam eles elementares ou avançados, ao longo da nossa carreira como engenheiros informáticos: é importante saber como funcionam, quais as vantagens e desvantagens de cada um, e por conseguinte em que cenários é que devemos aplicar cada um.

Os algoritmos presentes nesta página são, devido à sua natureza elementar, mais fáceis de programar: regra geral, não têm um conjunto muito complexo/extenso de instruções, e a lógica que os acompanha é relativamente simples.

Posto isto, vamos definir agora algumas noções úteis para o estudo que vamos fazer sobre algoritmos:

Abstrações Úteis?

A ordenação de itens de uma lista é feita através de uma chave: o problema associado a esta noção encontra-se no facto de cada item poder ter chaves (e propriedades em geral) diferentes, pelo que é da maior utilidade criar abstrações que nos permitam (re)utilizar o código de um dado algoritmo para mais que um tipo de item. Algumas abstrações clássicas, usualmente abordadas nas aulas teóricas da UC e que vamos também utilizar ao longo das próximas páginas, são as seguintes:

typedef int Item;
/* As barras (escaping) permitem escrever em varias linhas */
/* o que estamos a definir para não ficar tudo sobreposto */
#define key(A) (A)
#define less(A, B) (key(A) < key(B))
#define exch(A, B)  \
    {               \
        Item t = A; \
        A = B;      \
        B = t;      \
    }

#define compexch(A, B) \
    if (less(B, A))    \
        exch(A, B)

Selection Sort

Dentro dos algoritmos de ordenação elementares, um dos mais simples de compreender.

Pensando numa abordagem de ordenação crescente, começamos por procurar o elemento com menor chave do vetor, trocando-o com o primeiro elemento do mesmo. [O primeiro elemento do vetor diz-se agora ordenado], e não voltamos a tocar nele. Realizamos a mesma operação, com a procura agora a partir do segundo elemento da lista, e realizamos esta pesquisa até só restar a pesquisa que corresponde a passar apenas pelo último elemento da lista: nesse momento, a lista diz-se ordenada. A ordenação decrescente segue um processo análogo a este, trocando o elemento escolhido com o último do vetor em vez do primeiro.

void selection_sort(int a[], int left, int right) {
    int i, j;
    for (i = left; i < right; i++) {
        int aux, min = i;
        for (j = i + 1; j <= right; j++) { /* procura o menor */
            if (a[j] < a[min]) {
                min = j;
            }
        }

        aux = a[i]; /* troca elementos */
        a[i] = a[min];
        a[min] = aux;
    }
}

O tempo de execução deste algoritmo é quadrático ($O(n²)$): na verdade, é do tipo $n + (n - 1) + (n - 2) + ...$, que corresponde a uma soma geométrica do tipo $\sum_{i = 1}^{n} i$, de natureza quadrática. O melhor caso é igual ao pior, já que percorremos necessariamente todos os elementos que restam ordenar. A sua implementação trivial (disposta acima) não é estável, sendo contudo possível recriar o Selection Sort de forma a que apresente essa propriedade.

Insertion Sort

Mais um para a coleção de algoritmos simples, mesmo em relação aos restantes elementares, e que todos temos de saber.

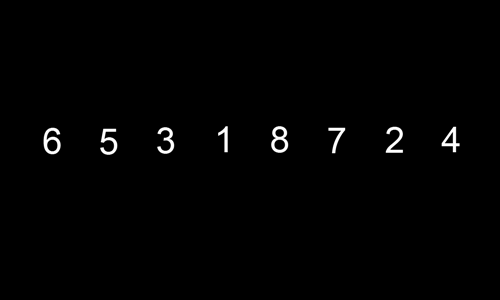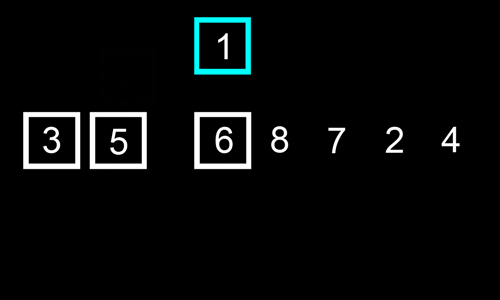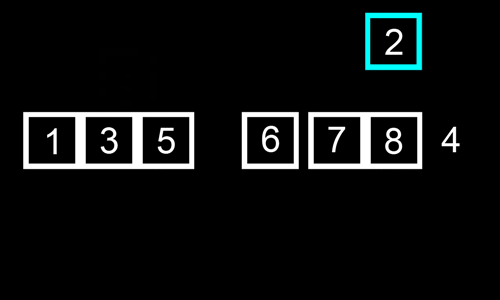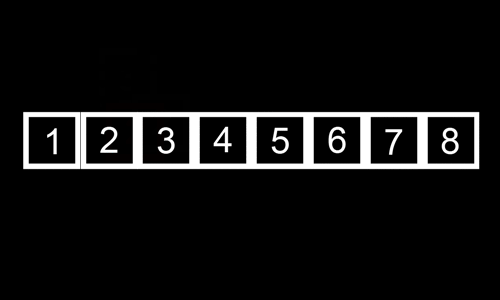
Podemos pensar neste algoritmo como alguém que joga às cartas e gosta de manter o seu baralho ordenado: sempre que recebe uma nova carta, percorre a lista do início para o fim (ou vice-versa), procurando colocar a carta entre um elemento com chave abaixo da sua e um acima da sua.

void insertion_sort(Item a[], int left, int right) {
    int i, j;
    for (i = left + 1; i <= right; i++) {
        Item v = a[i]; /* var auxiliar para guardar o valor de a[i] */
        j = i - 1;
        while (j >= left && less(v, a[j])) { /* percorrer o vetor */
                                             /* até encontrar o elemento menor que v */
            a[j + 1] = a[j];                 /* percorrer uma casa para a direita */
            j--;
        }
        a[j + 1] = v; /* guarda o valor na casa acima ao valor menor */
    }
}

O tempo de execução deste algoritmo também é quadrático: por cada carta a inserir, podemos ter que iterar por todo o vetor. Temos, contudo, uma diferença em relação ao Selection Sort: neste caso, o melhor caso é linear, já que a carta a inserir pode ser sempre no "topo do baralho"! É um algoritmo estável, já que inserir uma carta não altera as posições relativas das cartas já presentes no baralho.

Bubble Sort (Borbulhamento)

Este algoritmo já possui uma lógica mais interessante que os dois últimos, mantendo contudo alguma da simplicidade que caracteriza os algoritmos inseridos nesta categoria. Costuma ser abordado em FP, pelo que é natural que alguns de vocês tenham alguma memória (ainda que vaga) dele.

A sua lógica acaba por ser bastante straight-forward: começamos por pegar no primeiro elemento do vetor, seja esse o elemento $v$.O nosso objetivo aqui vai ser percorrer o vetor até encontrar um elemento com chave maior que a de $v$ - assim que o encontrarmos, passamos a considerar $v$ como esse movo elemento. Enquanto estivermos a pesquisar pelo vetor e não encontrarmos um elemento maior que $v$, vamos trocando $v$ com o elemento a comparar atualmente (tal como podem ver no gif acima). Quando se chega ao fim do vetor, dizemos que o elemento que lá (no fim) está encontra-se ordenado, e não voltamos a tocar nele. Realizamos estas trocas sucessivamente, até faltar ordenar apenas o primeiro elemento: nessa situação, o vetor está completamente ordenado.

void bubble_sort(Item a[], int left, int right) {
    int i, j;
    for (i = left; i < right; i++) {
        for (j = left; j < right + (left - i); j++) {
            compexch(a[j], a[j + 1]);
        }
    }
}

O algoritmo é também quadrático: temos sempre de percorrer o vetor até ao fim, de forma em tudo semelhante à referida na subsecção do Selection Sort. Tal como no Selection Sort, o melhor caso é também quadrático. É estável (ou pelo menos a implementação de bubble estável é trivial).

Shell Sort

O menos trivial dos quatro algoritmos apresentados nesta secção, corresponde a uma espécie de insertion sort (com coisas bastantes estranhas a acontecer lá pelo meio).

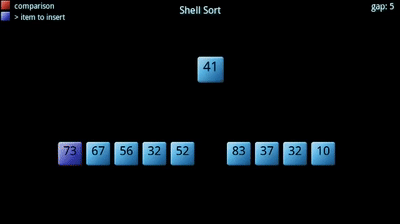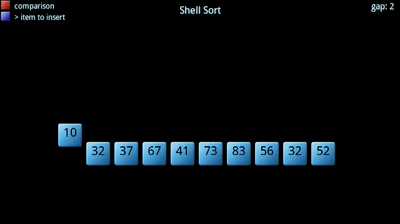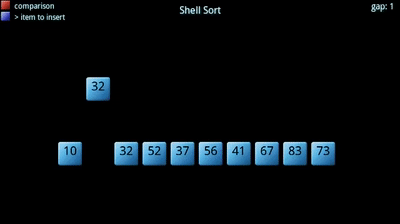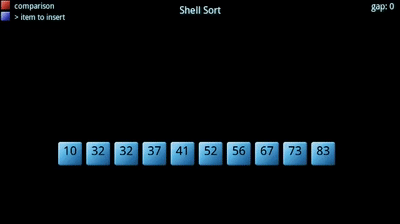
O algoritmo procura dividir um dado vetor em sub-vetores, que posteriormente são ordenados segundo um outro algoritmo de ordenação (normalmente o insertion sort). Tem uma constante, $h$, associada: $h$ corresponde ao número de sub-vetores a criar, tipicamente primo. Quanto maior o número de sub-vetores, menor o tamanho de cada um. A sequência e o $h$ "ótimos" ainda não foram encontrados!

void shell_sort(Item a[], int left, int right) {
    int i, j, h;
    for (h = 1; h <= (right - left) / 9; h = 3 * h + 1);

    for (; h > 0; h /= 3) {
        for (i = left + h; i <= right; i++) {
            Item v = a[i];
            int j = i;
            while (j >= left + h && less(v, a[j - h])) {
                a[j] = a[j - h];
                j -= h;
            }
            a[j] = v;
        }
    }
}

É efetivamente um algoritmo difícil de entender, pelo que aconselhamos, para além de ler (várias vezes) o código acima, a visualização do seguinte vídeo (e de outros relacionados com o tema):

A complexidade temporal do algoritmo está inerentemente ligada ao $h$ escolhido: o pior caso, contudo, é quadrático, sendo até possível encontrar melhores casos lineares. A complexidade média anda à volta de $n(\log{n})^2$. Não é um algoritmo estável.

Os slides que tipicamente acompanham a cadeira costumam incluir alguns exercícios para ajudar a entender o funcionamento dos algoritmos em questão. Mais ainda, aconselhamos também a consulta deste site para ajudar à visualização dos mesmos.