Algoritmos Elementares de Ordenação (Continuação)
Counting Sort
É um algoritmo frequentemente utilizado para ordenados elementos de um vetor em que sabemos que os mesmos podem aparecer repetidamente e as respetivas chaves são inteiros de valores relativamente baixos. Esta última "restrição" fará sentido mais à frente.
O procedimento-base do algoritmo é bastante simples: passa por guardar uma lista de ocorrências de cada chave durante o vetor. Percorrido o vetor inicial, preenche um vetor com as chaves ordenadas, tantas vezes quantas estas ocorrerem.
Este preenchimento do segundo vetor é realizado iterando o vetor auxiliar, que guarda a contagem de ocorrências de cada chave, do início para o fim, onde cada índice corresponde a uma chave! É então daqui a limitação de chaves com valores baixos: para valores muito grandes, deixa de fazer sentido utilizar o algoritmo (podemos pensar num vetor com 4 elementos, mas em que os vetores variam entre e - não faz sentido usar o counting sort).
/* Quantos elementos diferentes podem aparecer */
/* No exemplo da imagem acima, podem aparecer 9, os números entre 0 e 8 */
#define DISTINCT_ELEMENTS 9
/* Tamanho máximo do vetor que queremos ordenar */
#define MAX_SIZE 10
void counting_sort(int vec[], int left, int right) {
/* Vetor count que irá guardar quantas vezes aparece cada elemento */
int i, count[DISTINCT_ELEMENTS + 1];
/* Vetor auxiliar onde vamos guardar o vetor ordenado */
/* Mais à frente iremos ver como alocar dinamicamente
o espaço a ser alocado pelo mesmo (com malloc) */
int sorted_vec[MAX_SIZE];
/* Inicializar vetor count a zeros */
for (i = 0; i < DISTINCT_ELEMENTS; i++) {
count[i] = 0;
}
/* Para cada elemento de vec, somar 1 ao índice correspondente de count */
for (i = left; i < right; i++) {
count[vec[i] + 1]++;
}
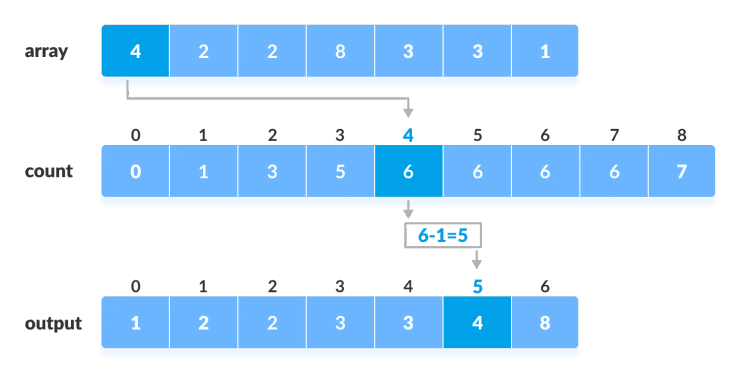
/* Para o exemplo da imagem, iremos obter o vetor: */
/* count = [0, 0, 1, 2, 2, 1, 0, 0, 0, 1] */
/* Passar a contagem de elementos para uma contagem cumulativa */
for (i = 1; i < DISTINCT_ELEMENTS + 2; i++) {
count[i] += count[i - 1];
}
/* Ficamos agora com um vetor count igual ao da imagem exemplo */
/* Cada índice indica a primeira posição onde iremos inserir o elemento,
daí existir uma posição no início que não está associada a nada. */
/* Para cada elemento do vetor original, vamos ver qual o índice inicial
no vetor ordenado. Para colocarmos corretamente valores repetidos no
vetor ordenado, temos de incrementar o valor no count, de forma a colocar
os repetidos na posição seguinte. */
for (i = left; i < right; i++) {
sorted_vec[count[vec[i]]++] = vec[i];
}
/* O vetor sorted_vec contém agora o resultado final, ordenado */
/* sorted_vec = [1, 2, 2, 3, 3, 4, 8] */
/* Finalmente, inserir o vetor ordenado de volta no vetor original */
for (i = left; i < right; i++) {
vec[i] = sorted_vec[i - left];
}
}A complexidade temporal do algoritmo é dada por , onde é o tamanho do vetor original e o valor máximo considerado. É um algoritmo estável, mas não é in-place: o vetor original não é alterado, é utilizado um vetor auxiliar, e é esse vetor que estará ordenado no fim.
Radix Sort
O radix sort baseia-se na estrutura dos elementos que pretende ordenar: ordena elementos processando cada dígito/bit/caracter do elemento atual separadamente (utilizando para esse efeito um outro algoritmo de ordenação, tipicamente o counting sort).
A sua complexidade temporal é , onde é a quantidade de elementos a ordenar e o tamanho da palavra a considerar: se estivermos a ordenar números com dígitos cada, por exemplo, teríamos e .
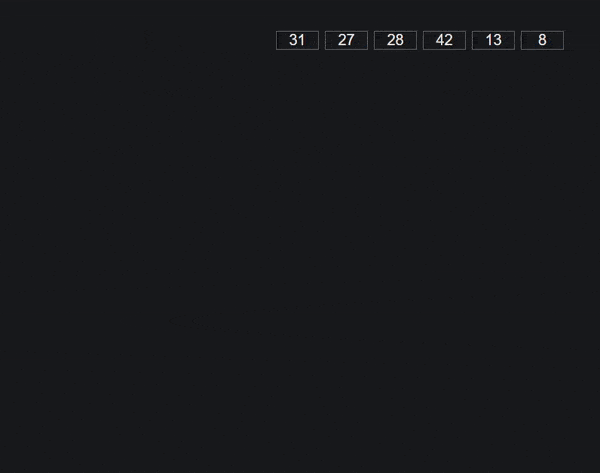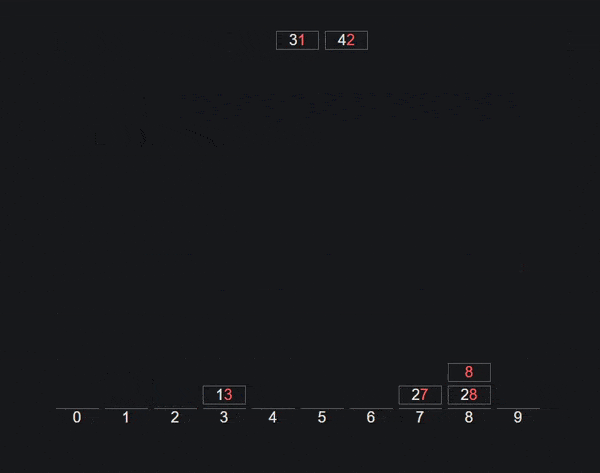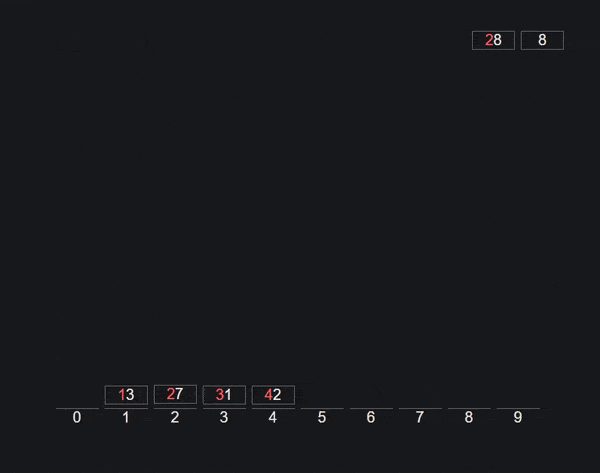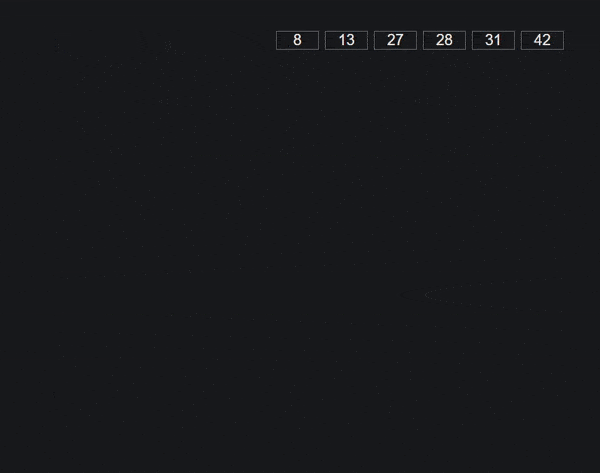
Em IAED vamos abordar as versões LSD e MSD do Radix sort: least significant digit e most significant digit, respetivamente.
RADIX LSD
Possui um funcionamento bastante simples: limita-se a aplicar o counting sort sucessivamente, dos dígitos menos significativos para os mais significativos.
/* Estamos a ordenar inteiros */
typedef int Item;
/* Existem 10 dígitos diferentes */
#define DISTINCT_ELEMENTS 10
/* Como exemplo, vamos usar números de 3 dígitos */
#define INT_LENGTH 3
/* Número máximo de elementos a ordenar */
#define MAX_SIZE 100
/* Obter dígito de num no índice digit_i */
int digit(int num, int digit_i) {
while (digit_i > 0) {
num = num / 10;
digit_i--;
}
return num % 10;
}
void radix_lsd(Item vec[], int left, int right) {
int i, curr_digit, count[DISTINCT_ELEMENTS + 1];
int sorted_vec[MAX_SIZE];
for (curr_digit = 0; curr_digit < INT_LENGTH; curr_digit++) {
/* Counting sort em cada dígito */
for (i = 0; i < DISTINCT_ELEMENTS; i++) {
count[i] = 0;
}
for (i = left; i < right; i++) {
count[digit(vec[i], curr_digit) + 1]++;
}
for (i = 1; i < DISTINCT_ELEMENTS + 2; i++) {
count[i] += count[i - 1];
}
for (i = left; i < right; i++) {
sorted_vec[count[digit(vec[i], curr_digit)]++] = vec[i];
}
for (i = left; i < right; i++) {
vec[i] = sorted_vec[i - left];
}
}
}Abaixo podem ver um exemplo da aplicação do Radix LSD:
RADIX MSD
Funcionamento análogo ao Radix LSD, com a diferença óbvia da ordenação ser "invertida": ordenamos do dígito mais significativo para o menos significativo.
void radix_msd(int a[], int l, int r, int w) {
int i = l, j = r;
if (r <= l || w > bitsword) {
return;
}
while (j != i) {
while (digit(a[i], w) == 0 && (i < j)) {
i++;
}
while (digit(a[j], w) == 1 && (j > i)) {
j--;
}
exch(a[i], a[j]);
}
if (digit(a[r], w) == 0) {
j++;
}
radix_msd(a, l, j - 1, w + 1);
radix_msd(a, j, r, w + 1);
}Abaixo podem ver um exemplo da aplicação do Radix MSD:
Mais uma vez, e tal como no final das duas últimas páginas, recomendo consultar a demonstração visual dos algoritmos referidos nesta página.