Análise Quantitativa
Análise Estatística
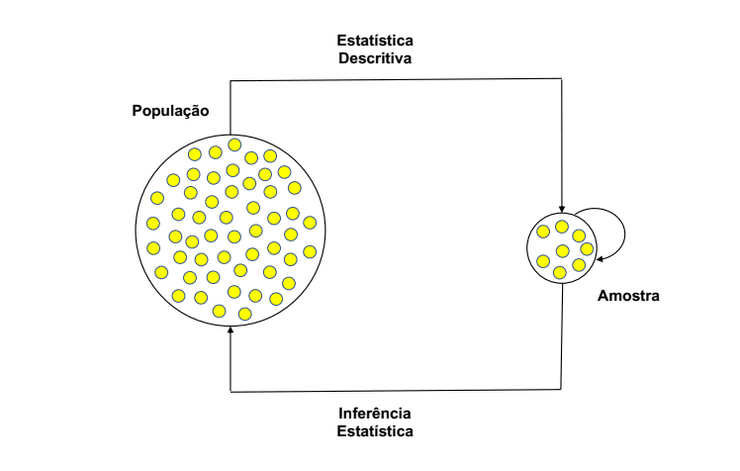
Quando estamos a trabalhar para uma empresa, esta não se importa com a amostra, contudo, temos que saber se a amostra é representativa da população ou não. Temos que perceber qual é a probabilidade da amostra ser característica da população.
Para tal temos que avaliar as variáveis.
Variáveis
Antes de fazermos inferências sobre os dados, é essencial examinar as variáveis. Mas porquê? Se recrutamos e-athletes e pessoas sem grande experiência para testar um videojogo, é normal que os e-athletes tenham mais sucesso do que as outras pessoas. Caso contrário, há algum bug no nosso jogo.
Assim, avaliar as variáveis ajuda a:
- Identificar potenciais erros
- Detetar padrões
- Garantir que as conclusões estão corretas
- Gerar e testar hipóteses
- Evitar problemas mais tarde
Podemos considerar variáveis dependentes ou independentes, como já tínhamos visto na aula passada. Variáveis dependentes são, por exemplo, o tempo, erros, SUS; enquanto que variáveis independentes são, por exemplo, cor, layout, idade, etc.
Escalas de Medida
Existem três tipos de escalas de medida:
-
Nominal
- Cor
- Marca
- Nome
-
Ordinal (a relação entre os pontos não é comparável)
- Leve, médio, pesado
- Satisfeito, neutro, insatisfeito
-
Contínua (mais usado em IPM)
- Idade;
- Altura;
- Peso;
- Tempo;
- Erros
Mensagens importantes
- É importante utilizarmos análise estatística para generalizar resultados a partir de uma amostra.
Segundo bake-off
Para o vídeo do segundo bake-off, não é necessário pôr a nossa análise estatística, porque não afeta minimamente a nota, no entanto, é recomendado.
-
Utilizamos estatística descritiva: é o primeiro passo para examinar dados
-
Tipos de variáveis e dados representam independentes/dependentes, nominais/ordinais/contínuas.
Estatística Descritiva
Para estatística descritiva, são importantes algumas fórmulas.
-
Média:
-
Soma dos quadrados das diferenças
-
Variância
-
Desvio-padrão
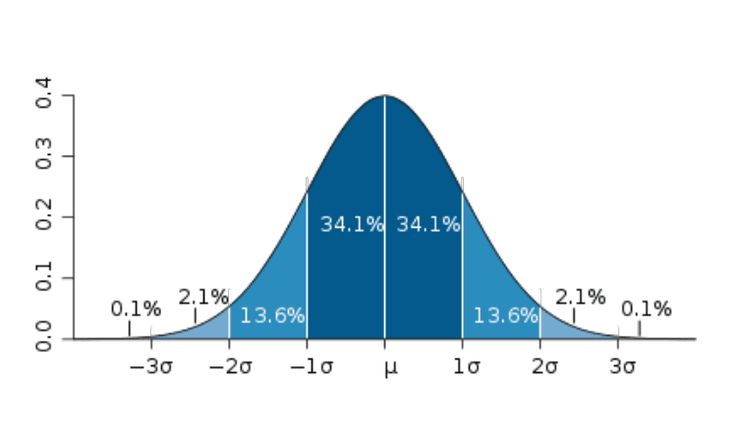
Desvio-Padrão
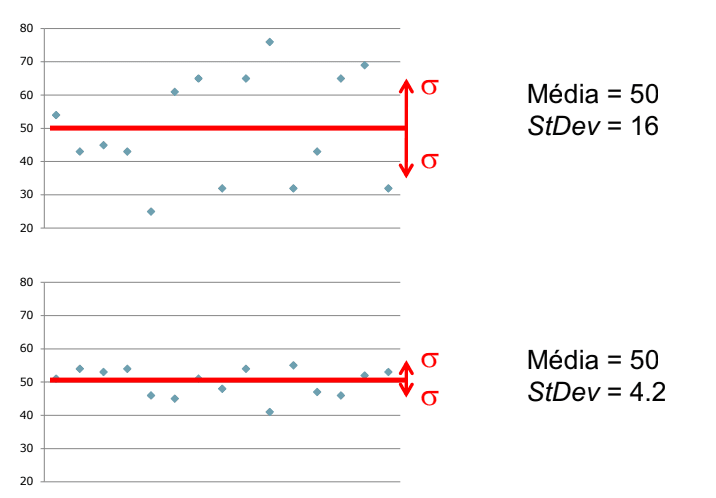
O desvio-padrão é muito importante para conseguirmos identificar se há uma variação muito grande entre os resultados dos nossos participantes e se há algum outlier.
Segundo bake-off
Para o segundo bake-off, vai ser tomado em conta o outlier, ou seja, a pessoa que está muito fora da média num sentido negativo. Contudo, o outlier apenas representa uma pessoa que, a meio do teste, se distraiu e começou a fazer outras coisas, ou seja, só em casos muito excessivos. Se houver algum caso destes, o grupo será descontado na nota final.
Mediana vs. Média
A mediana é calculada após ordenarmos todos os valores e encontrarmos o valor que está no meio, é muito útil ao compararmos a mediana e a média, pois, se houver uma diferença entre os dois, então há algo invulgar no nosso projeto.
Quartis
Os quartis ajudam a segmentar a população. Por exemplo, se tivermos uma amostra com os valores
sabemos que 25% corresponde ao primeiro 2, 50% corresponde ao 3 e 75% dos valores corresponde ao primeiro 9. Resumidamente, dividimos os valores da nossa amostra em 4 e vemos a que valor corresponde.
Moda
A moda corresponde ao valor mais comum, ou seja, ao valor mais repetido dentro da nossa amostra. É mais útil quando estamos a tratar de valores nominais, por exemplo, em resposta à pergunta "Qual o teu clube favorito?"
O quê? Quando?
-
Variáveis Nominais: moda
"Quantos preferem A, B ou C?"
-
Variáveis Ordinais: mediana, moda, quartis
"Nível de satisfação, de 1 a 5."
-
Variáveis Contínuas: média, desvio-padrão, mediana, quartis
"Tempo médio para fazer a tarefa."
Inferência Estatística
Ao completarmos uma iteração do nosso projeto, temos que verificar se a nossa solução cumpre os objetivos, ou seja, se os nossos critérios de usabilidade são atingidos.
Exemplo
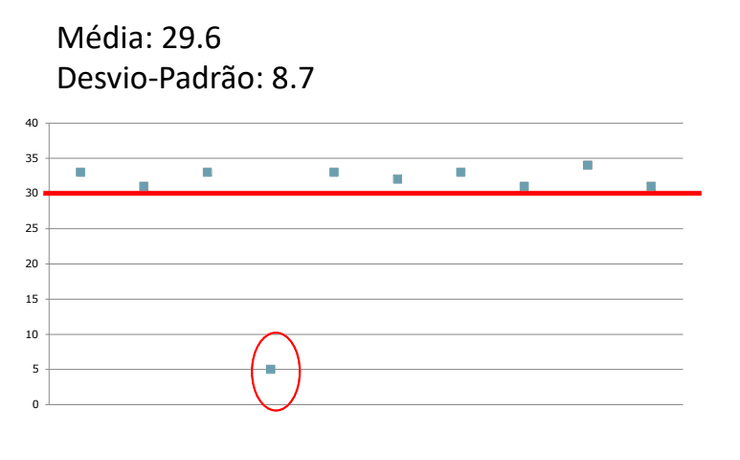
Ao acabarmos um projeto, pretendemos verificar se a nossa solução possibilita o nosso participante a terminar uma tarefa em menos do que 30 segundos
Ao fazemos testes com 10 utilizadores, reparamos que a média é 29,6 segundos, o que tecnicamente está dentro do nosso objetivo, visto que 29,6 é menor que 30. Contudo, ao avaliarmos o desvio-padrão, reparamos que toda a gente está entre os 30/35 segundos, tirando uma pessoa que conseguiu completar a tarefa em 5 segundos!
Se recorrermos ao mesmo teste, mas em vez de 10 utilizadores, tivermos 20 utilizadores, já será mais difícil ter uma média perto de 30 segundos, se só houver um outlier. Porém, se houver mais do que um, então já será mais complicado obtermos uma média correta.
Isto prova, exatamente, que as amostras nem sempre são viáveis por causa dos outliers, haverá sempre pelo menos um. Assim, temos que comparar a nossa média com os dados que obtivemos.
Então quais são os testes mais viáveis que podemos utilizar?
Há vários:
- Teste t-student
- Intervalos de Confiança
- Qui-Quadrado
- Coeficiente de correlação de Pearson
Testes de Hipótese
Existe um certo procedimento ao qual devemos recorrer de modo a que os nossos testes corram da melhor forma possível.
O primeiro passo refere-se à Escolha da amostra representativa, isto é, temos que escolher um grupo de pessoas que possam representar o nosso público-alvo, como vimos na última aula. Este grupo tem que ser relevante para o nosso produto.
O segundo passo refere-se à Formulação da hipótese nula (). A hipótese nula retrata um caso onde não há diferenças nenhumas, nada muda, por exemplo a mudança de menus não afeta o desempenho. Após a hipótese nula, temos que avaliar a hipótese experimental, , ou seja, diz o que queremos verificar, por exemplo, os novos menus melhoram o desempenho.
Procedimento - Grau de Confiança
Probabilidade de parecer que se verifica, mas afinal estarmos errados
Por outras palavras, representa a probabilidade de apanharmos o nosso utilizador fora do vulgar, o outlier.
Assim, podemos classificar o Grau de Confiança como:
Exemplo
Se tivermos , então, sabemos que temos um grau de confiança de 95%, que é bastante aceitável.
Por outro lado se tivermos um , sabemos que temos um grau de confiança de 99%, ou seja, temos um grau de confiança ainda melhor.
O terceiro passo refere-se à Realização dos testes, ou seja, à recolha de dados. Ao realizarmos os testes, temos que ter cuidado com o nosso número de amostras, visto que maiores amostras conferem melhores resultados. É importante relembrar Nielsen, que disse que o melhor número de participantes é 20, pois quanto mais pessoas houver, mais outliers haverá.
O último passo refere-se à Aplicação de tratamento estatístico. Ao fazer o nosso teste estatístico, vamos aferir se podemos rejeitar e aceitar . Mas, qual é o melhor teste para aplicarmos?
Quatro Testes Diferentes
warning
Os testes que vão ser apresentados foram escolhidos aleatoriamente, não são os melhores testes e há muitos mais
-
Intervalos de confiança: Comparar uma média com valor objetivo; Variáveis contínuas
-
Qui-quadrado: Comparar frequências esperada e observada; Variáveis normais
-
Coeficientes de correlação de Pearson: Relação entre variáveis dependentes
-
T-student para médias
T-student
William Sealy Gosset e T-student
William Sealy Gosset era um trabalhador para a Guinness que trabalhava para averiguar qual o melhor campo de cultivo através de testes A/B (mas com cerveja). Em 1908, este queria publicar um artigo sobre o seu estudo, mas não queria que o seu nome estivesse associado ao mesmo, então, publicou sobre o pseudónimo Student. Daí, nasceu o T-student e o seu nome.
O t-student pode ser usado com variáveis contínuas, como tempo, erros, altura, etc. Pode também ser usado para comparar duas médias, nomeadamente menus vs. atalhos, códigos-base vs. a nossa implementação, entre outros.
Segundo bake-off
Para o vídeo do segundo bake-off, não é necessário pôr a nossa análise estatística, porque não afeta minimamente a nota, no entanto, é recomendado.
O t-student para médias
As médias são todas iguais. Isto significa que, se rejeitarmos , podemos dizer que são diferentes com uma confiança de .
Existe uma série de pressupostos para o t-test:
- Há uma distribuição normal?
- Temos pelo menos 20 samples?
- O que estamos a medir está bem distribuído?
- Há uma variância similar?
- ...
Atenção que existe uma exceção para samples que estejam bem distribuídas. Se quisermos algo funcional, não queremos que o resultado esteja bem espalhado, queremos que exista uma flatline no 100.
O t-test é especialmente útil, pois conseguimos ver a olho todos os parâmetros.