Coordenação e Consenso
Exclusão mútua distribuída
Já fomos introduzidos ao problema da exclusão mútua em Sistemas Operativos (SO), que tem como objetivo garantir que dois processos/threads não acedem concorrentemente ao mesmo recurso (ex: ficheiro, bloco de memória, ...), uma vez que tal pode causar incoerências (ao tentarmos ler e escrever no mesmo espaço por ex.).
Em Sistemas Distríbuidos existe o mesmo problema: é necessário coordenar os processos de forma a garantir que não acedem simultaneamente ao mesmo recurso, mas com a diferença de que agora a exclusão mútua é distribuída, baseando-se na troca de mensagens.
Algoritmos de exclusão mútua
Consideramos um sistema de processos , que não partilham variáveis. Os processos acedem a recursos comuns, mas fazem-no numa secção crítica.
Os requisitos essenciais para exclusão mútua são:
- ME1 (safety): apenas um processo pode estar na secção crítica
- ME2 (liveness): os pedidos para entrar e sair da secção crítica eventualmente são bem sucedidos (esta condição previne deadlocks e starvation)
- ME3 (happened-before ordering): se um pedido para entrar na secção crítica ocorreu antes de outro, então a entrada é concedida nessa ordem.
Algoritmo do servidor central
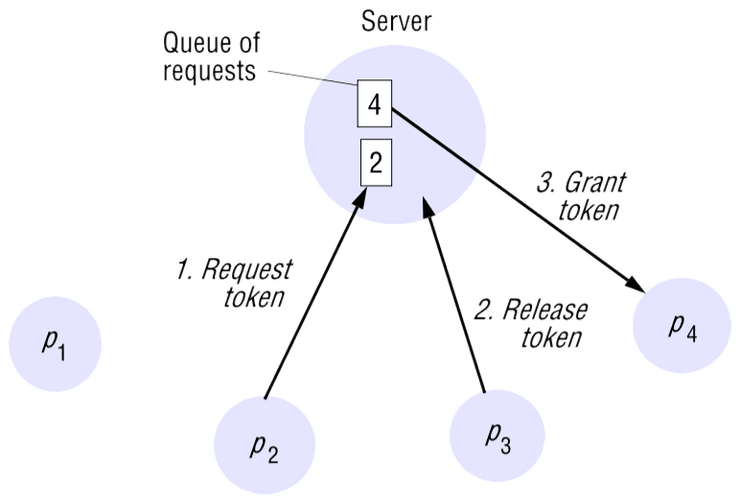
Esta é a forma mais simples de alcançar a exclusão mútua, utilizando um servidor que concede permissão para entrar na secção crítica.
Para entrar na secção crítica, um processo envia um pedido ao servidor e aguarda uma resposta deste. Conceptualmente, a resposta é uma chave que significa permissão para entrar na secção crítica. Se nenhum outro processo tiver a chave, então o servidor responde imediatamente, concedendo a chave. Se a chave estiver detida por outro processo, então o servidor não responde, mas coloca o pedido numa fila de espera. Quando um processo sai da secção crítica, envia uma mensagem ao servidor, devolvendo-lhe a chave.
Desvantagens:
- Pode existir sobrecarga do servidor.
- Se o servidor falhar, o sistema fica bloqueado.
- É necessário entregar a "chave" ao servidor para que este depois a passe a outro cliente (entregar diretamente ao próximo cliente seria muito mais eficiente)
Devemos assim tentar implementar uma solução descentralizada!
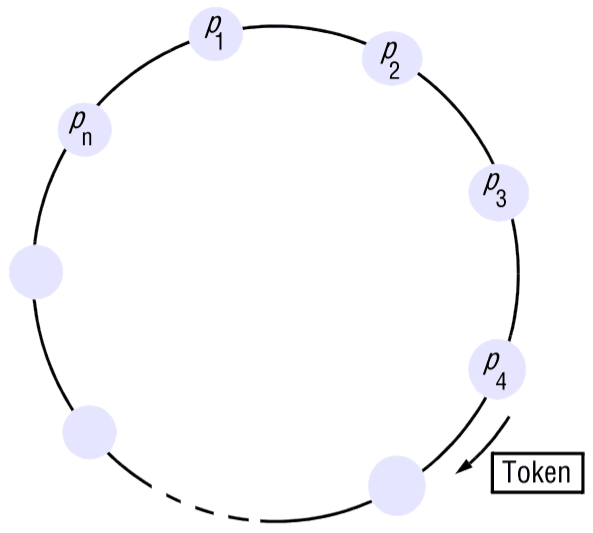
Algoritmo baseado em anel
Uma das formas mais simples de estabelecer exclusão mútua entre processos sem utilizar um processo adicional é organizá-los num anel lógico. Isto apenas requer que cada processo tenha um canal de comunicação com o próximo processo no anel, .
A ideia é que a exclusão mútua é concebida passando a chave de processo para processo numa única direção (por exemplo, no sentido horário) ao redor do anel. Se um processo não precisa de entrar na secção crítica quando recebe a chave, encaminha-a para o seu vizinho. Um processo que precise da chave espera até recebê-la (e retém-a após receber). Para sair da secção crítica, o processo encaminha a chave para o seu vizinho.
Algoritmo de Ricart and Agrawala
Este algoritmo utiliza 3 estados:
HELD: significa que temos acesso exclusivo à região críticaWANTED: não temos acesso mas queremos obtê-loRELEASED: não precisamos de aceder à região crítica
Se um processo deseja aceder à região, deve enviar requests a todos os outros clientes e esperar obter "OK" de todos estes. Se todos responderem afirmativamente, o processo recebe acesso exclusivo à região.
On initialization
state := RELEASED;
To enter the section
state := WANTED;
Multicast request to all processes; // É omitido o processamento dos requests
T := request’s timestamp;
Wait until (number of replies received = (N – 1)); // Espera receber N-1 OK's
state := HELD; // Temos acesso
On receipt of a request <T_i, p_i> at p_j (i != j)
// Se (já temos acesso) ou (queremos ter e enviámos o pedido há mais tempo),
// colocamos os pedidos em espera
if (state = HELD or (state = WANTED and (T, p_j) < (T_i, p_i)))
then
queue request from p_i without replying;
else
reply immediately to p_i;
end if
To exit the critical section
state := RELEASED;
reply to any queued requests;Exemplo
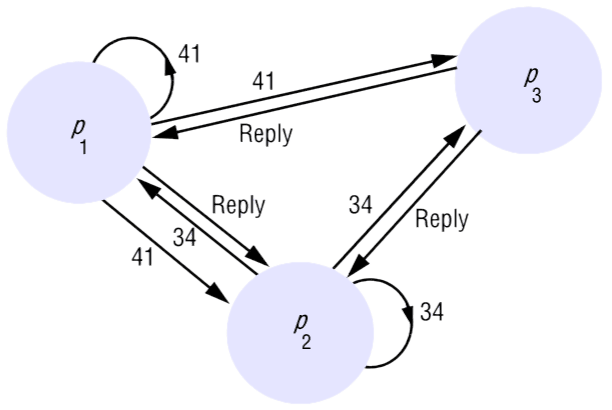
Para ilustrar o algoritmo, considere uma situação envolvendo três processos, , e , conforme mostrado na figura. Vamos supor que não está interessado em entrar na secção crítica, e que e solicitam entrada simultaneamente. O timestamp do pedido de é 41, e o de é 34.
Quando recebe os pedidos, responde imediatamente. Quando recebe o pedido de , verifica que o seu próprio pedido tem timestamp menor e, portanto, não responde, mantendo em espera. No entanto, verifica que o pedido de tem um timestamp menor do que o seu próprio pedido e, portanto, responde imediatamente. Ao receber esta segunda resposta, pode entrar na secção crítica. Quando decidir sair da secção crítica, responderá ao pedido de e concederá a sua entrada.
Este algoritmo já permite que a "chave" seja passada diretamente para outro cliente, mas tem 2 problemas:
- Não é tolerante a faltas
- Em vez de sobrecarregar o servidor, sobrecarrega todos os processos!
Cuidado
Poderíamos pensar que uma alternativa seria basear este algoritmo em prioridades em vez de timestamps, mas isto não funciona! Vejamos o seguinte exemplo:
Em (*), o processo com prioridade 0 responde com "OK" apesar de ter feito o pedido antes, visto que a sua prioridade é inferior à do cliente que pediu acesso. Desta forma, ambos recebem OK's e têm acesso "exclusivo" à zona crítica.
Algoritmo de Maekawa
Maekawa observou que, para um processo entrar numa secção crítica, não é necessário que todos os seus peers concedam o acesso (só precisa de obter permissão de um subconjunto destes).
Este algoritmo associa um voting set (também chamados quóruns) a cada processo , onde . Os sets são escolhidos de forma a que, para todo :
- – há pelo menos um membro comum entre quaisquer dois voting sets
- – de forma a ser justo, todos os voting sets têm o mesmo tamanho
- Cada processo está contido em dos voting sets
Nota
Maekawa demonstrou que a solução ótima (que minimiza e permite que os processos alcancem a exclusão mútua) tem e . Como não é trivial calcular os sets ótimos , uma forma simples de derivar estes sets tal que , é colocar os processos numa matriz por e ser a união da linha e coluna que contém .
Cada processo pode votar num pedido de acesso à região crítica, mas não pode votar em mais que um em simultâneo, o que origina a seguinte propriedade:
Propriedade fundamental
Em qualquer par de quóruns, há sempre interseção em pelo menos um processo, o que implica que dois pedidos concorrentes nunca podem ambos receber os votos de quóruns completos.
K = |V_i| ~ sqrt(N)
On initialization
state := RELEASED;
voted := FALSE;
For p_i to enter the critical section
state := WANTED;
Multicast request to all processes in V_i;
Wait until (number of replies received = K);
state := HELD;
On receipt of a request from p_i at p_j
if (state = HELD or voted = TRUE)
then
queue request from p_i without replying;
else
send reply to p_i;
voted := TRUE;
end if
For p_i to exit the critical section
state := RELEASED;
Multicast release to all processes in V_i;
On receipt of a release from p_i at p_j
if (queue of requests is non-empty)
then
remove head of queue – from p_k, say;
send reply to p_k;
voted := TRUE;
else
voted := FALSE;
end ifEste algoritmo consegue distribuir a carga, ou seja, não existe um processo que recebe todos os pedidos, mas tem um grande problema: sofre de interbloqueio (deadlock-prone).
deadlock-prone
Considere 3 processos, , e , com , e . Se os três processos solicitarem simultaneamente acesso à seção crítica, então é possível que:
- responda a si mesmo e meta em espera
- responda a si mesmo e meta em espera
- responda a si mesmo e meta em espera
Desta forma, cada processo recebeu apenas uma resposta (de dois pedidos), e nenhum pode prosseguir.
Nota
O algoritmo pode ser adaptado de forma a tornar-se deadlock-free. No protocolo adaptado, os processos colocam na fila de espera pedidos pendentes em ordem happened-before, garantindo assim que o requisito ME3 também seja satisfeito.
(ver o exemplo ilustrativo de Ordem Total baseada em acordo coletivo)
Comparação dos algoritmos
Terminologia:
- Bandwith usage : total de mensagens trocadas entre enter /exit por um mesmo cliente
- Client delay : tempo para um processo entrar numa secção crítica livre
- Synchronization delay : tempo entre exit por um processo e enter por outro que estava à espera
| Algoritmo | Bandwith usage | Client delay | Synchronization delay |
|---|---|---|---|
| Centralizado | |||
| Ricart and Agrawala | |||
| Maekawa |
* assumindo que os 2 quóruns se intercetam em apenas 1 processo
Distribuição de carga:
- Centralizado: tudo passa pelo servidor, possível sobrecarga
- Ricart and Agrawala: todos os processos são sobrecarregados
- Maekawa: cada pedido apenas afeta um subconjunto de processos (quórum)
Tolerância a falhas:
- Todos assumem rede fiável! Nenhum tolera perdas de mensagens
- Centralizado: não tolera falha do servidor, mas tolera falha de cliente
em estado
RELEASED - Ricart and Agrawala: nenhum processo pode falhar
- Maekawa: cada pedido tolera falhas dos processo que não estejam no quórum
Eleição de líder
Tal como vimos anteriormente, muitos algoritmos distribuídos precisam de atribuir cargos especiais a certos processos. Por exemplo, na variante "servidor central" dos algoritmos para exclusão mútua, o servidor é escolhido entre os processos que precisam de utilizar a secção crítica. É necessário um algoritmo de eleição para esta escolha, sendo essencial que todos os processos concordem com a mesma.
É necessário assegurar principalmente 2 propriedades:
- E1 (safety): todos os processos escolhem o mesmo líder (tipicamente o processo com id maior)
- E2 (liveness): a execução do algoritmo é finita
Ao longo deste capítulo, iremos assumir que:
- O detetor de falhas é perfeito, ou seja, nunca diagnostica erradamente um processo como morto
- Os processos não recuperam, ou seja, não voltam ao ativo depois de morrerem
Eleição em anel
Este algoritmo é adequado para um conjunto de processos organizados num anel lógico. Cada processo tem um canal de comunicação com o próximo processo no anel, , e todas as mensagens são enviadas no sentido horário ao redor do anel.
Funcionamento do algoritmo
Quando um processo p decide iniciar uma eleição:
- Marca-se como participante
- Prepara uma mensagem
election(id(p))e envia-a para o próximo anel
Quando um processo p recebe uma mensagem election(id):
- Se o id na mensagem é superior ao identificador local:
preencaminha-a ao próximo e marca-se como participante. - Se o id na mensagem é inferior e
painda não participava: substitui o id na mensagem pelo dep, reencaminha-a ao próximo e marca-se como participante. - Se o id na mensagem é o de
p, entãoptorna-se o novo líder! Marca-se como não participante e envia mensagemelected(id(p))ao próximo no anel.
Quando um processo p recebe uma mensagem elected(id):
- Aprende que o novo líder é aquele indicado na mensagem, reencaminha a mensagem e marca-se como não participante.
- Se o id na mensagem for
p, não faz nada (o algoritmo terminou).
Exemplo
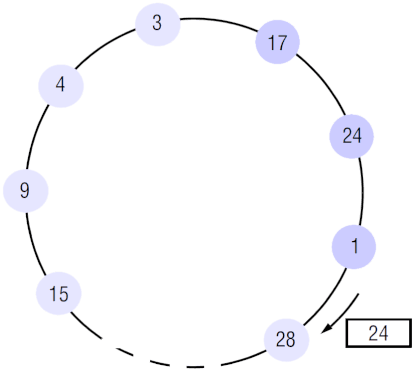
A execução do algoritmo começou no nó 17 e até agora participaram 3 nós: 17, 24
e 1 (realçados com uma cor ligeiramente diferente). O nó 1 envia election(24)
já que o seu id é menor que o da mensagem. Ao receber election(24), o nó 28
envia election(28), pois possui um id maior. Assumindo que o maior id é 28,
os restantes nós irão reencaminhar esta mensagem até chegar ao emissor. Após a
receção, o nó 28 irá emitir a mensagem elected(28). O algoritmo termina quando
esta última mensagem dá uma volta completa ao anel e regressa ao líder (28).
No caso em que apenas um processo dá início ao processo de eleição, podem ser geradas até mensagens.
Justificação
Ao começar no processo seguinte ao que possui o maior id:
- irão ser trocadas mensagens até chegar ao processo com maior id
- mensagens para circular todo o anel com a mensagem
election(max(id))até regressar ao processo com maior id, que irá emitir a mensagemelected(max(id)) - mensagens para circular novamente todo o anel e terminar ao regressar ao emissor
Nota
Se todos os processos decidirem começar o processo de eleição ao mesmo tempo, o algoritmo tem uma complexidade temporal quadrática.
Eleição em anel por torneio
- Os processos procuram um líder num horizonte que duplica em cada turno
- Em cada turno o número de competidores vai sendo reduzido para metade
- Isto resulta na execução de turnos para uma complexidade total de
Algoritmo "Bully"
O objetivo deste algoritmo é, tal como anteriormente, eleger o processo com maior identificador.
Tem alguns pressupostos:
- existem tempos máximos conhecidos para a comunicação (sistema síncrono; canais fiáveis)
- os processos podem falhar
- todos os processos conhecem os identificadores dos restantes
Existem 3 tipos de mensagens trocadas neste algoritmo:
election: que assinala o início de uma eleiçãoanswer: serve de resposta a uma mensagemelectioncoordinator: assinala o id do processo elegido (o novo coordenador)
Funcionamento do algoritmo
Um processo inicia uma eleição quando se apercebe, através de timeouts, que o coordenador falhou (vários processos podem descobrir isto simultaneamente):
- se for o processo com id mais alto:
- elege-se a si próprio e envia uma
coordinatormessage para todos os processos com id mais baixo
- elege-se a si próprio e envia uma
- se não:
- envia a todos os processos com ids mais altos uma
electionmessage:- se não receber nenhuma
answermessage, considera-se o coordenador e envia umacoordinatormessage a todos os processos com id mais baixo - se receber, espera durante um período de tempo por uma mensagem
coordinatore caso não receba nenhuma, começa uma nova eleição
- se não receber nenhuma
- envia a todos os processos com ids mais altos uma
Quando um processo receber uma coordinator message:
- regista o id recebido na mensagem e passa a tratar esse processo como coordenador
Quando um processo recebe uma election message:
- envia de volta uma
answermessage - começa uma nova eleição (a não ser que já tenha começado uma)
Quando um novo processo vem substituir um outro crashed:
- começa uma nova eleição:
- se tiver o id mais alto: decide que é o líder e anuncia-o (mesmo que o atual líder esteja a funcionar, daí ser chamado bully)
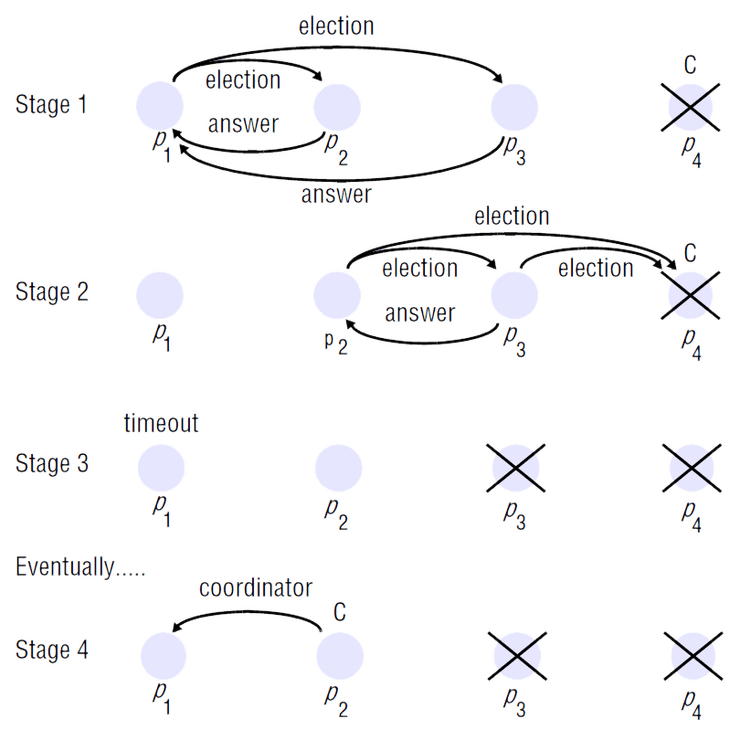
Exemplo
O processo deteta a falha do líder e começa uma eleição (stage 1).
Ao receber a mensagem election do , os processos e enviam
answer's de volta e começam as suas próprias eleições. envia uma answer
ao mas não recebe do uma (stage 2).
decide assim que é o líder, mas antes de enviar a mensagem coordinator a
e , falha (stage 3).
Quando o timeout de dispara (assumimos que é menor que o de ),
este começa uma nova eleição, já que não recebeu uma mensagem coordinator.
O vai enviar mensagens a e e ao não obter resposta elege-se
como líder, notificando (stage 4).
No melhor caso, o processo com o segundo maior identificador percebe a falha
do coordenador e elege-se imediatamente, e envia mensagens coordinator.
No pior caso, o processo com o identificador mais baixo é o primeiro a detetar a falha do coordenador. Assim, processos iniciam eleições simultaneamente, cada um enviando mensagens para os processos com identificadores mais altos. Desta forma, o algoritmo requer mensagens.
Nota
O algoritmo não garante cumprir a condição E1 se os processos que falharam forem substituídos por outros com os mesmos identificadores, visto que é possível que dois processos anunciem simultaneamente que são coordenadores. Além disso, esta condição pode ser violada se os valores de timeout forem imprecisos.
Algoritmo do "Luís"
O professor desenhou um algoritmo bastante simples, que consiste em ter um detetor de falhas que notifica todos os processos sempre que algum falha:
-
Inicialização:
-
Quando um processo () falha:
Bully vs "Luís":
Algoritmo do Luís:
- simples
- modular
- menos eficiente pois obriga a detetar falhas em processos que não são candidatos a líder
Algoritmo Bully:
- Mistura deteção de falhas com eleição de líder
- Cada processo apenas precisa de detetar falhas de outros com id maior
Deteção de falhas
Todos estes algoritmos têm um grande problema: assumem que a deteção de falhas é perfeita. Só assim conseguem garantir que todos os nós funcionais elegem o mesmo líder (ou seja, garantir a safety do algoritmo).
Uma deteção de falhas perfeita implica que:
- um processo funcional nunca é diagnosticado como falhado
- a falha é sempre detetada
Mas para se fornecer tais garantias é preciso que:
- o sistema seja síncrono, para que se possa detetar as falhas com exatidão com recurso a temporizadores
- não hajam falhas na rede
Por outro lado, se a deteção de falhas não for perfeita:
- os processos podem discordar sobre a identidade do líder
- podem existir vários líderes ao mesmo tempo
O ideal seria construirmos algoritmos que são tolerantes a falhas, de forma a não dependerem de uma deteção perfeita.
Deteção de falhas "alguma-vez" perfeita
O detetor pode temporariamente errar, mas há um momento a partir do qual volta a estar correto (por ex. declarando um processo como falhado mas mais tarde reconhecendo que está ativo). Um detetor com estas características é designado por "alguma-vez" (do inglês "eventually") perfeito.
Problema do Consenso
O consenso é um dos problemas mais difíceis e estudados de Sistemas Distribuídos. Foi provado que, num sistema assíncrono em que podem ocorrer falhas, este problema não tem solução (resultado conhecido como FLP).
Definição de Consenso
Dado um conjunto de processos:
- Cada processo propõe um valor (input)
- Todos os processos decidem o mesmo valor (output)
Notas:
- O valor decidido deve ser um dos valores propostos
- invalidando assim uma solução que decide sempre um valor por omissão independentemente dos inputs dados
- Pode ser qualquer um dos valores propostos:
- Não tem de ser o valor proposto por mais processos
- Não existe qualquer tipo de hierarquia de processos ou critério de qualidade que distinga os valores (i.e. não existem valores nem processos melhores que os outros)
Tipos específicos de consenso
Note que já utilizámos consenso anteriormente:
- na exclusão mútua, os processos concordam sobre o processo que pode entrar na secção crítica
- na eleição de líder, os processos concordam sobre o processo eleito
- no multicast totalmente ordenado, os processos concordam sobre a ordem de entrega das mensagens
Existem diversos protocolos para tipos específicos de consenso. No entanto, nesta secção vamos considerar formas mais gerais de consenso, analisando características e soluções comuns.
Podemos concluir assim três propriedades do Consenso:
- Terminação: todos os processos correctos decidem ("alguma-vez")
- Acordo uniforme: se dois processos decidem, decidem o mesmo valor
- Integridade: o valor decidido (output) foi proposto por um processo
Quanto a soluções para este problema em sistemas:
- síncronos: ou seja, onde é possível concretizar um detetor de falhas perfeito, iremos abordar o algoritmo FloodSet
- assíncronos: ou seja, onde é possível concretizar um detetor de falhas "alguma-vez" perfeito, não iremos abordar nenhum algoritmo, mas podem consultar o algoritmo "Paxos" do Lamport
Falhas bizantinas
Os processos podem falhar de formas arbitrárias (falhas bizantinas), enviando valores aleatórios para os restantes processos (estes valores aleatórios podem resultar de bugs ou operações maliciosas).
Nesta cadeira não iremos estudar algoritmos que têm este tipo de falhas em consideração. Se tiveres interesse em aprender mais recomendamos o vídeo introdutório do Martin Kleppmann ao "Byzantine generals problem" e o PBFT Consensus Algorithm.
Floodset Consensus
A ideia essencial deste algoritmo é cada processo enviar para todos os outros o seu valor (input), de forma a que no fim todos conheçam todos os valores possíveis e possam tomar a mesma decisão de forma determinística.
O funcionamento do algoritmo é baseado em rondas:
- em cada ronda, cada processo faz broadcast do seu valor
- ao receber um valor de outro processo, adiciona-o ao seu conjunto
- ao fim de rondas, é escolhido o output com base num critério
determinístico utilizado por todos os processos
- em que é o número de processos que pode falhar
Pseudocódigo
// Send only values that have not been sent
NOTA: o critério utilizado neste algoritmo para a escolha do output foi encontrar o valor mínimo, mas pode ser qualquer critério!
Exemplo
Exemplo de execução com :
Algumas notas acerca do algoritmo:
- Pressupõe um sistema síncrono
- se um processo não recebe o valor de outro processo no turno então o processo falhou de certeza (e não participa nos próximos turnos)
- É possível adaptar o algoritmo de forma a utilizar um detetor de falhas perfeito:
- Caso um processo não tenha recebido o valor de um processo num turno , apenas avança para o turno caso o detetor de falhas declare como falhado
- Em alguns casos, caso não ocorram falhas, é possível terminar em menos turnos
Propriedade
Qualquer algoritmo desenhado para resolver o consenso permitindo até falhas, requer pelo menos rondas de trocas de mensagens, independentemente da forma como foi construído.
Problemas relacionados
Iremos agora abordar dois exemplos de problemas que são semelhantes ao problema do Consenso e que podem ser utilizados para o resolver ou utilizá-lo na construção da sua solução.
Coerência Interativa
O problema da coerência interativa é outra variante de consenso, na qual cada processo propõe um único valor. O objetivo do algoritmo é fazer com que os processos corretos concordem com um vetor de valores, um para cada processo. Por exemplo, o objetivo poderia ser para cada processo de um grupo obter a mesma informação sobre os estados respectivos (de cada processo).
- Conjunto de processos
- Cada processo propõe um valor ()
- Todos os processo decidem o mesmo vetor ()
- O vetor decidido tem uma entrada por cada processo em que:
- ou
- ou
Propriedades:
- Terminação: todos os processos correctos decidem ("alguma-vez")
- Acordo uniforme: se dois processos decidem, decidem o mesmo vetor
- Integridade: se o processo não falhar,
Pseudocódigo das implementações
Consenso usando Coerência Interativa:
Quando Consenso.propoe(valor):
CoerenciaInteractiva.propoe(valor)
Quando CoerenciaInteractiva.decide(vector):
valor = primeiraEntradaDiferenteDeNull(vector);
Consenso.decide(valor)
Coerência Interativa usando consenso:
// este codigo é executado por todos os processos
fun PRONTO(vector):
se para todo o p_x: p_x não pertence a falhados e tivermos vector_proposta[x] != null
retorna VERDADEIRO
caso contrário
retorna FALSO
Init:
falhados = {}
para cada valor de i < N
vector_proposta[i] = null;
Quando falha(p_x):
falhados = falhados U {p_x}
Quando IC.propoe(valor_i)
DifusaoFiavel.envia(p_i, valor_i)
Quando DifusaoFiavel.entrega(p_j, valor_j)
vector_proposta[j] = valor_j;
Quando PRONTO(vector_proposta)
Consenso.propoe(vector_proposta) // só propõe uma vez
Quando Consenso.decide(vector)
IC.decide(vector)Derivar Consenso a partir de Coerência Interativa
Por vezes é possível derivar uma solução para um problema utilizando uma solução para outro. Esta propriedade é muito útil porque aumenta a nossa compreensão dos problemas e economiza esforço de implementação.
Suponha que existem as seguintes soluções para o consenso (C) e para a consistência interativa (IC):
- retorna o valor de decisão do processo numa execução da solução para o problema do consenso, onde são os valores propostos pelos processos
- retorna o j-ésimo valor no vetor de decisão do processo numa execução da solução para o problema da consistência interativa, onde são os valores propostos pelos processos
Caso a maioria dos processos estejam corretos, construímos uma solução executando IC para produzir um vetor de valores em cada processo, e depois aplicando uma certa função sobre os valores do vetor para derivar um único valor:
Nota
Em sistemas com falhas, resolver o consenso é equivalente a resolver o multicast confiável e totalmente ordenado: dada uma solução para um, podemos resolver o outro. Implementar o consenso com base em operações de multicast confiável e totalmente ordenado é trivial.
Dado um grupo de processos , para alcançar o consenso, cada processo executa . Em seguida, cada processo escolhe , onde é o primeiro valor que .
Difusão com terminação
- Conjunto de processos
- Um processo pré-definido envia uma mensagem
- Se o processo é correto, todos os processos corretos entregam
- Se o processo falha, os processos entregam ou
- Todos os processos corretos entregam o mesmo valor (ou ou )
Propriedades:
- Terminação: todos os processos correctos decidem ("alguma-vez")
- Acordo uniforme: se dois processos decidem, decidem o mesmo valor
- Integridade: se o processo não falhar,
Pseudocódigo das implementações
Difusão com Terminação usando Consenso:
Quando ConsensoPropoe(v) no processo i
i.DifusaoComTerminacaoEnvia(v)
Para todo o i
i.DifusaoComTerminacaoEntrega(v_i)
Escolhe v_final como sendo o menor v_i: v_i != null
ConsensoDecide(v_final)Consenso usando Difusão com Terminação:
No emissor:
Quando DifusaoComTerminacao(m)
DifusaoFiavelEnvia(m)
ConsensoPropoe(m)
No restantes processos, executa um e apenas um destes passos:
Quando DifusaoFiavelEntrega(m)
ConsensoPropoe(m)
Quando suspeita a falha do processo "s"
ConsensoPropoe(null)
Em todos os processos:
Quando ConsensoDecide(v)
DifusaoComTerminacaoEntrega(m)Impossibilidade em sistemas assíncronos
As soluções para o consenso que abordámos assumem que o sistema é síncrono, ou seja, assumem que um processo falhou se não lhes enviou uma certa mensagem dentro da ronda desejada (atraso máximo excedido).
Fischer et al. [1985] provaram que nenhum algoritmo pode garantir alcançar o consenso num sistema assíncrono, visto que os processos podem responder a mensagens com latências arbitrárias, fazendo com que um processo que realmente falhou seja indistinguível de um lento.
Note que este resultado não significa que os processos não podem alcançar o consenso distribuído num sistema assíncrono. Este permite que o consenso possa ser alcançado com alguma probabilidade maior que zero, confirmando o que sabemos na prática (por exemplo, existem sistemas de transações assíncronos que têm alcançado o consenso regularmente há anos).
Ainda assim, existem diversas técnicas (não abordadas em aula) para contornar o resultado da impossibilidade. Por exemplo:
- Mascarar falhas: envolve técnicas como o uso de armazenamento persistente e replicação de componentes para ocultar falhas, permitindo que os processos continuem a funcionar corretamente
- Consenso usando detetores de falhas: envolve o uso de detetores de falhas (não perfeitos) em sistemas assíncronos para alcançar o consenso, seja considerando processos não responsivos como falhados ou permitindo que processos suspeitos continuem a participar no consenso
- Consenso usando randomização: envolve introduzir aleatoriedade no comportamento dos processos para neutralizar os efeitos negativos dos sistemas assíncronos, permitindo que o consenso seja alcançado em tempo (esperado) finito
Referências
- Coulouris et al - Distributed Systems: Concepts and Design (5th Edition)
- Secções 15.1-15.5
- Departamento de Engenharia Informática - Slides de Sistemas Distribuídos (2023/2024)
- SlidesTagus-Aula03a
- SlidesTagus-Aula04
- SlidesAlameda-Aula08