Replicação e Tolerância a Faltas
- Introdução a sistemas replicados
- Registos partilhados e replicados
- Teorema CAP
- Coerência fraca
- Coerência forte
- Consenso e Replicação
- Referências
Introdução a sistemas replicados
A replicação consiste no processo de manter cópias de dados e software de um serviço em várias máquinas.
Benefícios de replicar um sistema
- melhor disponibilidade: mesmo que alguns nós falhem ou fiquem indisponíveis devido a falhas na rede, o sistema continua disponível
- melhor desempenho e escalabilidade:
- Podem existir cópias mais próximas do cliente
- Algumas operações não precisam de ser executadas sobre todo o sistema, podendo ser executadas apenas sobre algumas cópias (distribuindo assim a carga e aumentando a escalabilidade)
Linearizabilidade
Uma das garantias essenciais que um sistema replicado tem que assegurar é a coerência. O ideal seria um cliente ler a versão mais recente do recurso sempre que lê de uma réplica (mesmo que essa versão tenha sido escrita noutra réplica). Um critério de coerência que podemos utilizar é a linearizabilidade. Antes de definirmos o que é, é necessário ter em conta o seguinte quanto à ordenação de operações:
- As operações realizadas sobre um sistema replicado não são instantâneas:
- A operação é invocada por um cliente, executada durante algum tempo e o cliente só recebe a resposta mais tarde.
- Se uma operação X começa depois de outra operação Y acabar, então X ocorre depois de Y
- Se uma operação X começa antes de outra operação Y acabar, então X é concorrente com Y
Exemplo
- A concorrente com B
- A anterior a C
- B anterior a C
- C concorrente com D
- C anterior a E
- D concorrente com E
Definição
Um sistema replicado diz-se linearizável se e só se:
-
Existe uma serialização virtual que respeita o tempo real em que as operações foram invocadas, isto é:
- Se ocorre antes de (em tempo real), então tem de aparecer antes de na serialização virtual. (se e forem concorrentes, a serialização pode ordená-las de forma arbitrária)
-
A execução observada por cada cliente é coerente com essa serialização (para todos os clientes), ou seja:
- Os valores retornados pelas leituras feitas por cada cliente refletem as operações anteriores na serialização
Exercício
Considere os seguintes exemplos em que um cliente escreve sobre um inteiro replicado. Quais das execuções são serializáveis?
Exemplo 1:
Exemplo 2:
Exemplo 3:
R: Apenas o 1º exemplo:
Registos partilhados e replicados
Um registo suporta duas operações:
- Escrita:
- uma escrita substitui o valor da anterior
- apenas um cliente pode escrever no registo num dado instante, ou seja, as escritas são ordenadas
- Leitura:
- múltiplos clientes podem ler do registo ao mesmo tempo
Tipos de registos
Lamport definiu três modelos de coerência para registos:
-
Safe:
- Se uma leitura não for concorrente com uma escrita, lê o último valor escrito
- Se for, pode retornar um valor arbitrário
-
Regular:
- Se uma leitura não for concorrente com uma escrita, lê o último valor escrito
- Se for, ou retorna o valor anterior ou o valor que está a ser escrito
- NOTA: este tipo de registo não é linearizável, já que enquanto decorre uma escrita, é possível que leituras seguidas leiam sequências incoerentes de valores (primeiro o novo valor e depois o antigo)
-
Atomic:
- Equivalente a linearizabilidade quando aplicada a registos
- O resultado da execução é equivalente ao resultado de uma execução em que todas as escritas e leituras ocorrem instantaneamente num ponto entre o início e o fim da operação
Exemplos
- registo "Unsafe":
- registo "Safe":
- registo "Regular":
- registo "Atomic":
De onde surgiu a ideia de um registo "safe"?
Considere um registo com o valor (em binário: ) e que se quer escrever o valor (em binário: ). Se não existir um mecânismo de sincronização que impeça o leitor de ler o registo durante a escrita, a leitura pode retornar um dos seguintes valores:
- =
- =
- =
- =
(já que os bits são alterados individualmente em instantes diferentes)
Registos distribuídos
Uma forma de implementar registos distribuídos é a seguinte:
- Cada processo mantém uma cópia do registo
- Cada registo guarda um tuplo
<valor, versão> - Para executar uma operação (leitura ou escrita), os processos trocam mensagens entre si
É possível implementar este funcionamento de forma a que seja tolerante a faltas e não bloqueante!
Algoritmo ABD
Registo regular (com um só escritor):
-
Escrita:
- O escritor incrementa o número de versão e envia o tuplo
<valor, versão>para todos os processos. - Quando os outros processos recebem esta mensagem, atualizam a sua cópia do registo (caso seja uma versão mais recente que a local) e enviam uma confirmação ao escritor.
- A operação termina quando o escritor receber resposta de uma maioria.
- O escritor incrementa o número de versão e envia o tuplo
-
Leitura:
- O leitor envia uma mensagem a todos os processos solicitando o tuplo mais recente
- Cada processo envia o seu tuplo
<valor, versão> - Após receber resposta de uma maioria, retorna o valor mais recente e atualiza o valor local (caso necessário)
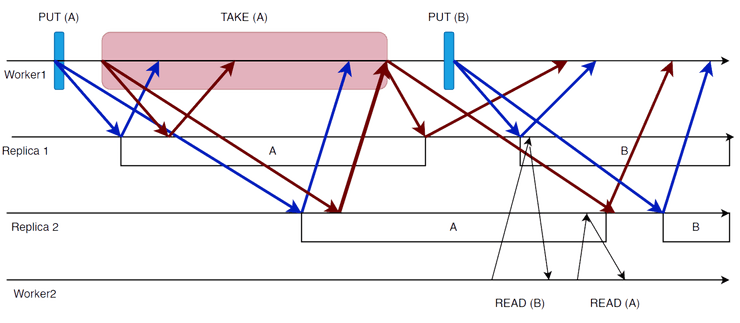
Exemplo
O algoritmo não é atómico
Tal como ilustrado no diagrama, é possível obter leituras diferentes consoante as réplicas que contactamos (lendo , depois e novamente), violando o princípio da linearizabilidade.
Registo atómico (com um só escritor):
-
Escrita:
- Idêntico ao anterior.
-
Leitura:
- Executa o algoritmo de leitura anterior mas não retorna o valor
- Executa o algoritmo de escrita, usando o valor lido
- Retorna o valor lido apenas após a escrita ter terminado
Espaço de Tuplos
Espaço de Tuplos "Linda"
Consiste num espaço partilhado que contêm um conjunto de tuplos (ex: <"A">,
<"A", 1>, <"A", "B">) e que suporta 3 operações:
Put: adiciona um tuplo (sem afetar os tuplos existentes) no espaçoRead: retorna o valor de um tuplo (sem afetar o conteúdo do espaço)Take: também retorna um tuplo mas remove-o do espaço- Tanto
ReadcomoTakesão bloqueantes caso o tuplo não exista - Tanto
ReadcomoTakeaceitam wildcards:Read(<"A", *>)pode retornar<"A", 1>ou<"A", "B">
Como o Take é bloqueante, pode ser usado para sincronizar processos:
- Elege-se um tuplo especial, por ex.
<lock>. - Cada processo remove o tuplo do espaço antes de aceder à região crítica e volta a colocá-lo no fim, garantindo assim exclusão mútua
- Conseguimos assim através de uma única interface partilhar memória e sincronizar processos
Enquanto que nos registos uma escrita fazia override do valor antigo, aqui o
processo equivalente é realizar um Take seguido de um Put (os tuplos são
imutáveis). O Take permite fazer operações que em memória partilhada requerem
uma instrução do tipo
compare-and-swap.
Nota
Note que as operações Put, Read e Take são conhecidas como out, rd e
in no modelo Linda, usamos estes nomes mais descritivos como simplificação.
Xu-Liskov
Muitas das implementações de espaços de tuplos adotam uma solução centralizada. Isto tem vantagens em termos de simplicidade, mas tais soluções não são tolerantes a falhas nem escaláveis.
Xu-Liskov é uma implementação distribuída e tolerante a faltas do "Linda".
Algumas observações prévias
-
A tolerância de faltas pressupõe um serviço de filiação que gere o grupo de réplicas:
- Quando uma réplica falha, a filiação do grupo é alterada
-
Sendo assim, quando o algoritmo espera por "todas" as respostas ou pela maioria delas, refere-se à filiação do grupo num dado instante.
-
Esta alteração dinâmica da filiação é um problema bastante complexo por si só e portanto não vai ser abordado
-
Os autores optam por usar UDP (portanto pode haver perda de mensagens), sendo o próprio algoritmo responsável por retransmitir mensagens.
- Solução modular: usar TCP
O objetivo dos autores com este design era obter a solução mais eficiente e com o menor tempo de resposta possível, mas assegurando linearizabilidade.
Funcionamento do algoritmo
Put:
- The requesting site multicasts the
putrequest to all members of the view; - On receiving this request, members insert the tuple into their replica and acknowledge this action;
- Step 1 is repeated until all acknowledgements are received. For the correct operation of the protocol, replicas must detect and acknowledge duplicate requests, but not carry out the associated put operations.
Read:
- The requesting site multicasts the
readrequest to all members of the view; - On receiving this request, a member returns a matching tuple to the requestor,
- The requestor returns the first matching tuple received as the result of the operation (ignoring others);
- Step 1 is repeated until at least one response is received.
Take:
Phase 1: Selecting the tuple to be removed
- The requesting site multicasts the
takerequest to all members of the view; - On receiving this request, each replica acquires a lock on the associated tuple
set and, if the lock cannot be acquired, the
takerequest is rejected; - All accepting members reply with the set of all matching tuples;
- Step 1 is repeated until all sites have accepted the request and responded with their set of tuples and the intersection is non-null;
- A particular tuple is selected as the result of the operation (selected randomly from the intersection of all the replies);
- If only a minority accept the request, this minority are asked to release their locks and phase 1 repeats.
Phase 2: Removing the selected tuple
- The requesting site multicasts a remove request to all members of the view citing the tuple to be removed;
- On receiving this request, members remove the tuple from their replica, send an acknowledgement and release the lock;
- Step 1 is repeated until all acknowledgements are received.
Visto que este algoritmo foi projetado para minimizar o delay :
- Operações
readapenas bloqueiam até que a primeira réplica responda ao pedido - Operações
takebloqueiam até o final da fase 1, quando o tuplo a ser excluído foi acordado - Operações
putpodem retornar imediatamente
No entanto, isto introduz níveis inaceitáveis de concorrência. Por exemplo, uma
operação read pode aceder a um tuplo que deveria ter sido excluído na segunda
fase de uma operação take. Assim, são necessárias as seguintes restrições adicionais:
- As operações de cada worker devem ser executadas em cada réplica na mesma ordem em que foram emitidas pelo worker
- Uma operação
putnão deve ser executada em nenhuma réplica até que todas as operaçõestakeanteriores, emitidas pelo mesmo worker, tenham sido concluídas em todas as réplicas (na visão do mesmo)
Nota
Operações
takebloqueiam até o final da fase 1, quando o tuplo a ser excluído foi acordado
Note que isto é uma otimização para minimizar a latência, no algoritmo original o worker fica bloqueado até o final da fase 2. Esta otimização não faz parte do projeto.
Imaginemos que o Read não era bloqueante, ou seja, ou retornava o tuplo
ou "null". O sistema continuaria a ser linearizável? Não, pois seria possível:
- Um cliente executa
Putde um tuplo - Um cliente executa
Read(t)várias vezes, concorrentemente com oPut - Se o leitor recebe respostas de réplicas diferentes em cada
Read, pode ler e de seguida "null"
Quanto ao Take, é possível que dois processos tentem fazer Take do mesmo tuplo
concorrentemente e nenhum consiga a maioria (deadlock). Para resolver este problema
introduz-se um fator de aleatoriedade: cada processo repete o seu pedido um tempo
aleatório depois (solução não determinista).
Teorema CAP
Segundo este teorema, é impossível um sistema apresentar simultaneamente:
- Consistency (coerência)
- Availability (disponibilidade)
- Partition-tolerance (tolerância a partições na rede)
Apenas pode ter 2 destas propriedades (quaisquer duas).
Coerência fraca
Nesta secção, vamos explorar técnicas de replicação para tornar os serviços altamente disponíveis. O objetivo é dar aos clientes acesso ao serviço (com tempos de resposta razoáveis) durante o máximo de tempo possível, mesmo que alguns resultados não respeitem a consistência sequencial.
Garantias de sessão
- Read Your Writes:
- Se um Read procede um Write numa sessão, então o valor de é incluído em
- Monotonic Reads:
- Se um Read precede um Read numa sessão, tem que incluir todos os Writes completos incluídos em (mas pode ter alterações mais recentes)
- Writes Follow Reads:
- Se um Read precede um Write numa sessão e é executado no servidor , então qualquer servidor que inclui também inclui qualquer Write incluido em na ordem em que foram escritos
- Monotonic Writes:
- Se um Write precede um Write numa sessão, então qualquer servidor que inclua também inclui na ordem em que foram escritos
| Guarantee | Session state updated on | Session state checked on |
|---|---|---|
| RYR | Write | Read |
| MR | Read | Read |
| WFR | Read | Write |
| MW | Write | Write |
Pseudocódigo de operações de escrita e leitura
Write(W,S) = {
if WFR then
check S.vector dominates read-vector
if MW then
check S.vector dominates write-vector
wid := write W to S
write-vector[S] := wid.clock
}
Read(R,S) = {
if MR then
check S.vector dominates read-vector
if RYW then
check S.vector dominates write-vector
[result, relevant-write-vector] := read R from S
read-vector := MAX(read-vector, relevant-write-vector)
return result
}Propagação epidémica (gossip propagation)
De forma a introduzir o conceito de propagação de informação, vamos pensar sobre a forma menos coordenada possível de fazê-lo:
- Periodicamente, cada processo contacta os outros e envia-lhes informação/atualizações
- A informação é assim propagada como uma espécie de "rumor" (do inglês gossip)
- Apresenta a grande vantagem de ser totalmente descentralizada, balanceando a carga por todos os processos
Ao propagar informação desta forma surgem, naturalmente, duas questões essenciais:
- Por que ordem devem ser aplicadas as atualizações recebidas dos outros processos?
- Se um processo contacta primeiro uma réplica R1 e depois outra R2, que garantias mínimas devem existir?
Pensemos no exemplo em que existem três réplicas R1, R2 e R3 e que se está a executar uma aplicação de preparação de slides de forma cooperativa:
- Em R1 um cliente executa a instrução "criar círculo", que é propagada para R2
- Em R2 outro cliente executa a instrução "pintar círculo", que é propagada para R3
- R3 recebe primeiro a instrução "pintar círculo" antes de "criar círculo", o que pode gerar um erro
Outro exemplo:
- Em R1 um cliente executa a instrução "label=distribúidos" e propaga-a para R2
- Em R2 um cliente apercebe-se da gralha e corrige-a: "label=distribuídos"
- R3 recebe primeiro a instrução executada em R2 e só depois a executada em R1
- Se aplicar as atualizações por esta ordem, a correção da gralha fica sem efeito
A grande maioria dos sistemas de propagação epidémica aplica as atualizações de forma a respeitar a relação aconteceu-antes, ou seja, respeita a ordem causal dos acontecimentos.
E no caso dos clientes móveis?
- Um cliente muda a sua password na réplica R1
- Muda para a réplica R2 antes da alteração ser propagada
- Não consegue utilizar a sua nova password
Existem sistemas capazes de garantir a relação aconteceu-antes para clientes móveis, enquanto que outros oferecem garantias ainda mais fracas como as garantias de sessão apresentadas acima.
Todas estas garantias podem ser atingidas com o uso de relógios lógicos (pouco eficiente).
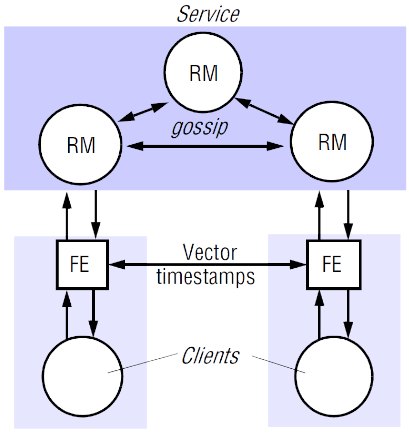
Lazy Replication - gossip architecture
Foi proposta em 1922 e inspirou muitos dos sistemas fracamente coerentes dos dias de hoje. Tem como objetivo:
- garantir acesso rápido aos clientes
- mesmo quando existem partições na rede
- com o trade-off de sacrificar a coerência
O nome gossip vem de as réplicas propagarem as alterações periodicamente em background, como se fossem boatos.
O algoritmo oferece coerência fraca, mas assegura duas propriedades:
- Monotonic reads
- mesmo que o cliente aceda a réplicas diferentes
- O estado das réplicas respeitam a ordem causal das alterações
- se uma modificação depende de outra , a réplica nunca executa antes de
Interação cliente-réplica
-
Cada cliente mantém um timestamp vetorial denominado
- vetor de inteiros, um por réplica
- reflete a última versão acedida pelo cliente
-
Em cada contacto com uma réplica, é enviado também o : (pedido, )
-
A réplica devolve (resposta, )
- em que é o timestamp vetorial que reflete o estado da réplica
- se a réplica estiver atrasada em relação ao cliente, espera até se atualizar para devolver uma resposta (caso seja uma leitura)
-
Cliente atualiza de acordo com , confrontando cada entrada de com a correspondente de
- se ,
-
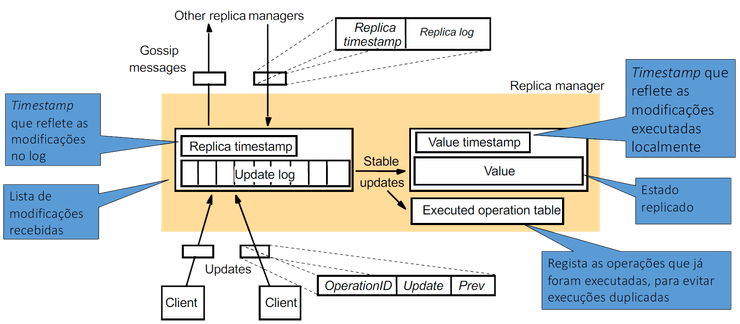
Cada réplica mantém também localmente um update log
- uma réplica pode já ter recebido uma modificação mas não a poder executar devido a ainda não ter recebido/executado dependências causais, pelo que a mantém em estado pendente no log
- pode assim propagar modificações individuais para as outras réplicas, mantendo o update no log até receber confirmação de todas elas
Quando uma réplica recebe um pedido de leitura:
- verifica se
- se sim, retorna o valor atual juntamente com o
- se não, o pedido fica pendente até estar atualizada
Quando uma réplica recebe um pedido de modificação:
- verifica se já o executou e em caso afirmativo descarta-o
- incrementa a entrada do seu em uma unidade
- atribui à modificação um novo timestamp calculado por:
- com a entrada substituída pelo novo valor calculado acima (gerando assim um timestamp único para este update)
- adiciona a modificação ao log e retorna o novo timestamp ao cliente
- espera até se verificar para executar o
código localmente
- garantindo assim que a execução respeita a ordem causal
- quando finalmente executar o pedido, atualiza o
- para cada entrada : se ,
Para propagar as modificações:
- periodicamente, cada gestor de réplica contacta outro gestor
- envia de forma ordenada a as modificações do seu log que estima que não tem
- para cada modificação que recebe:
- se não for duplicada, adiciona ao seu log
- atualiza o seu
- assim que , executa a modificação
- NOTA: As modificações não são apenas propagadas desta forma (comunicação periódica). Quando um gestor de réplicas descobre que precisa de uma certa atualização para processar um pedido, este pode pedi-la diretamente.
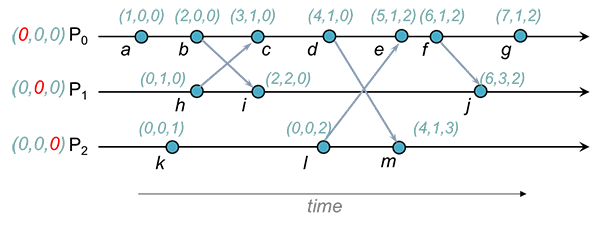
Aconteceu-antes vs protocolo gossip
Enquanto que quando estudámos a relação aconteceu-antes vimos que 3 tipos de eventos atualizavam os timestamps vetoriais:
- Eventos locais genéricos
- Envio de uma mensagem
- Receção de uma mensagem
No gossip apenas existe um tipo de eventos que causa esta atualização: Updates
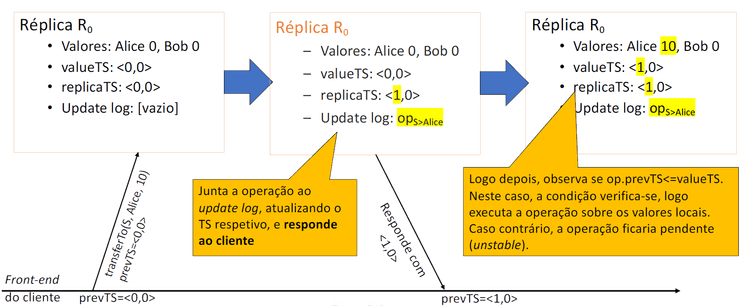
Exemplo
Imaginemos um sistema com 2 réplicas e , em que ambas mantêm saldos de contas bancárias. As contas da Alice e Bob começaram com saldo nulo e mais tarde receberam transferências de uma conta (que assumimos que contava com saldo suficiente para realizar ambas as transferências). Cada operação foi aceite por uma réplica diferente:
:
- aceite por com e
:
- aceite por com e
Execução da primeira operação:
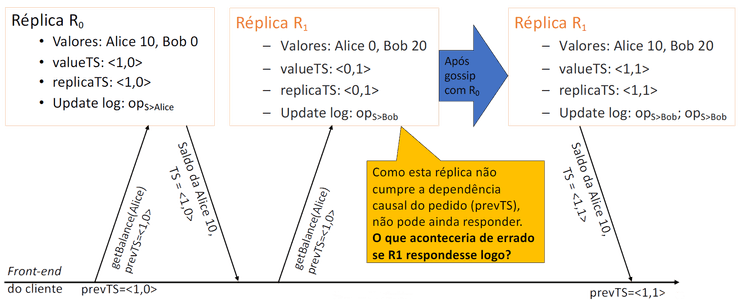
Execução de reads de réplicas diferentes:
Nota
Os clientes também podem comunicar diretamente entre si. Visto que estas comunicações podem originar relações causais entre operações realizadas no serviço, os clientes devem incluir os seus timestamps nestas mensagens de forma a que os destinatários consigam fazer merge dos timestamps. Assim, estas relações causais podem ser inferidas corretamente pelas réplicas do serviço.
Existem outros tipos de algoritmos para suportar operações que requerem modelos de coerência mais fortes, como por exemplo:
- Forced operations (total e causal)
- Immediate operations
As atualizações immediate-ordered são aplicadas numa ordem consistente em relação a qualquer outra atualização em todos os gestores de réplicas. Esta ordenação é utilizada porque, por exemplo, uma atualização forced e outra causal que não têm uma relação happened-before podem ser aplicadas em ordens diferentes nos diversos gestores de réplicas.
Estas garantias de ordenação não são abordadas nesta cadeira.
Algoritmo de Bayou
No sistema de Lazy Replication assume-se que as operações concorrentes são comutativas, ou seja, independentemente da ordem pela qual são aplicadas, o resultado final é o mesmo (por ex: "desenhar círculo" e "alterar cor da linha"). Se as operações não forem comutativas, é necessário utilizar primitivas mais fortes (forced/immediate).
O Bayou introduz uma solução para reconciliar automaticamente réplicas divergentes:
- Ordenar operações concorrentes por uma ordem total
- Cancelar as operações que foram executadas por uma ordem diferente
- Re-aplicar estas operações pela ordem total, aplicando uma função de reconciliação que é específica da aplicação
- As operações podem ser codificadas de forma a facilitar a reconciliação automática
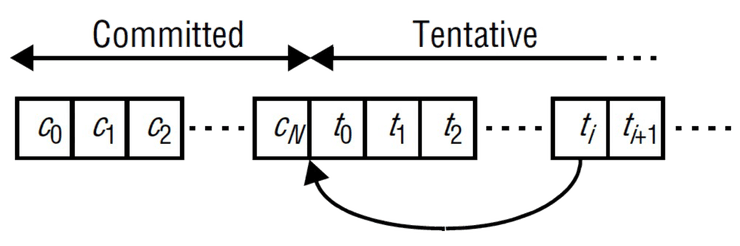
Updates: tentativo e commit
- Quando se faz um update, ele fica marcado como tentativo
- podendo ainda sofrer alterações nesta fase
- Quando o update é commited, a sua ordem já não pode ser alterada
- quem decide a ordem é tipicamente uma réplica especial, o primário
- quando um update é commited, as outras réplicas podem por isso ter que o ordenar
Na figura acima, tornou-se commited. Todas as atualizações tentative após precisam de ser desfeitas; é então aplicado após e de a e , etc., reaplicados após .
Exemplo de operação
Bayou_Write(
update = {insert, Meetings, 12/18/95, 1:30pm, 60min, "Budget Meeting"},
dependency_check = {
query = "SELECT key FROM Meetings WHERE day = 12/18/95
AND start < 2:30pm AND end > 1:30pm",
expected_result = EMPTY
},
mergeproc = {
alternates = {{12/18/95, 3:00pm}, {12/19/95, 9:30am}};
newupdate = {};
FOREACH a IN alternates {
# check if there would be a conflict
IF (NOT EMPTY (SELECT key FROM Meetings WHERE day = a.date
AND start < a.time + 60min AND end > a.time))
CONTINUE;
# no conflict, can schedule meeting at that time
newupdate = {insert, Meetings, a.date, a.time, 60min, "Budget Meeting"};
BREAK;
}
IF (newupdate = {}) # no alternate is acceptable
newupdate = {insert, ErrorLog, 12/18/95, 1:30pm, 60min, "Budget Meeting"};
RETURN newupdate;
}
)CRDTs (Conflict-Free Replicated Datatypes)
Um CRDT é uma estrutura de dados que é replicada em vários computadores numa rede, com as seguintes características:
- A aplicação pode atualizar qualquer réplica de forma independente, concorrente e sem precisar de comunicar com outras réplicas (ou seja, sem coordenação, ao contrário da abordagem operational transformation usada por Bayou)
- Um algoritmo (que faz parte da própria estrutura de dados) resolve automaticamente quaisquer inconsistências que possam surgir entre réplicas
- Embora as réplicas possam ter estados diferentes num determinado momento, é garantido que eventualmente irão convergir
Pequeno exemplo de um contador (CRDT) que apenas suporta as operações "increment" e "read":
// Replica i
increment() {
value[i]++;
}
read() {
return SUM k: 1..N_REPLICAS (value[k])
}
merge_with_replica_j() {
for k: 1..N_REPLICAS {
i.value[k] = max(i.value[k], j.value[k])
}
}Os CRDTs foram apresentados em aula apenas como uma curiosidade, se tiveres interesse em aprender mais recomendamos a palestra do Martin Kleppmann na QCon London 2018.
Coerência forte
Tolerância a faltas
Existem duas estratégias principais:
- Recuperação "para trás":
- guardar o estado do sistema de forma periódica ou em momentos relevantes, utilizando um algoritmo de salvaguarda distribuída
- quando os processos falham, são relançados o mais rapidamente possível
- os novos processos recomeçam a partir do último estado guardado
- solução tipicamente designada por "checkpoint-recovery"
- Recuperação "para a frente":
- são mantidas várias cópias (réplicas) do processo
- quando é feita uma alteração a uma réplica, esta deve ser propagada para todas as outras de forma a estarem atualizadas/sincronizadas
- se uma réplica falha, o cliente pode passar a utilizar outra
- estrutura de dados replicada:
- registo (algoritmo ABD)
- espaço de tuplos (Xu-Liskov)
- qualquer estrutura de dados que ofereça uma interface remota (exige algoritmos de replicação genéricos, tema deste capítulo)
De forma resumida:
- na recuperação para trás os estados guardados pelos vários processos que falharam devem estar mutuamente coerentes
- na recuperação para a frente os estados das réplicas que sobrevivem devem estar mutuamente coerentes.
Iremos analisar dois algoritmos de replicação genéricos (por recuperação para a frente):
- Primário-secundário
- Replicação de máquina de estados
Objetivo: assegurar linearizabilidade (coerência forte).
Algoritmo Primário-secundário (esboço)
- É eleito um processo como primário (sendo outro eleito em caso de falha)
- Os pedidos dos clientes são enviados para o primário
- Quando o primário recebe um pedido:
- executa-o
- propaga o estado para os secundários e aguarda confirmação de todos
- responde ao cliente
- (processa o próximo pedido que estiver na fila)
Vantagem: Suporta operações não determinísticas (primário decide o resultado).
Desvantagens:
- Se o primário produzir um valor errado, o erro vai ser propagado para as réplicas
- Se o detetor de falhas não for perfeito, pode existir mais que um primário concorrentemente, havendo o risco dos estados divergirem
Replicação de máquina de estados (esboço)
- Os clientes enviam os pedidos para todas as réplicas
- Os pedidos são ordenados por ordem total
- Todas as réplicas processam os mesmos pedidos, pela mesma ordem
- assume-se que as operações são determinísticas, de forma a todas as réplicas ficarem idênticas
- Cada réplica responde ao cliente (o número de respostas pelo qual o cliente aguarda depende das suposições de falhas)
Vantagem: Se uma réplica produzir um valor errado, não afecta as outras.
Desvantagens:
- As operações necessitam de ser determinísticas.
- Se o detetor de falhas não for perfeito, pode ser impossível estabelecer uma ordem total dos pedidos
Abstrações para a construção de sistemas replicados
Construir sistemas replicados com estes algoritmos é bastante complicado e complexo, pelo que iremos falar de algumas abstrações sobre as quais podemos construir de forma a facilitar a implementação dos mesmos.
| Aplicação |
|---|
| Difusão Atómica |
| Sincronia na Vista |
| Ordem FIFO e Causal |
| Difusão Fiável Uniforme |
| Difusão Fiável Regular |
| Canais Perfeitos |
| TCP ou UDP |
Canais Perfeitos
-
Garante a entrega de mensagens ponto a ponto de forma ordenada, caso nem o emissor nem o destinatário falhem
-
Implementação prática: retransmitir a mensagem até que a receção desta seja confirmada pelo destinatário
Difusão Fiável
-
Permite difundir uma mensagem com a garantia de que ou todos os destinatários a recebem ou nenhum recebe
-
Duas variantes: Regular e Uniforme
Difusão Fiável Regular
Propriedades:
- Seja uma mensagem enviada para um grupo de processos por um elemento do grupo
- Validade: se um processo correto envia então eventualmente entrega
- Não-duplicação: nenhuma mensagem é entregue mais que uma vez
- Não-criação: se uma mensagem é entregue então foi enviada por um processo correto
- Acordo: se um processo correto entrega então todos os processos corretos entregam
Algoritmo:
- O emissor envia a mensagem usando canais perfeitos para todos os membros do grupo
- Quando um membro do grupo recebe a mensagem, entrega-a à aplicação e reenvia-a para todos os membros do grupo
Difusão Fiável Uniforme
Propriedades:
- Seja uma mensagem enviada a para um grupo de processos por um elemento do grupo
- Validade, Não-duplicação e Não-criação tal como Difusão Regular
- Acordo: se um processo entrega então todos os processos corretos entregam
Algoritmo:
- O emissor envia a mensagem usando canais perfeitos para todos os membros do grupo
- Quando um membro do grupo recebe a mensagem, reenvia-a para todos os membros do grupo
- Quando um membro receber uma mensagem de membros distintos, entrega a mensagem à aplicação
- Em que é o número de processos que pode falhar
Sincronia na Vista
Vista: conjunto de processos que pertence ao grupo:
- Novos membros podem ser adicionados dinamicamente
- Um processo pode sair voluntariamente do grupo ou ser expulso caso falhe
Propriedades:
- Permite alterar a filiação de um grupo de processos de uma forma que facilita a tolerância a faltas
- A evolução do sistema é dada por uma sequência totalmente ordenada de vistas
- Exemplo:
- Um processo é considerado correto numa vista se faz parte dessa vista
e de
- Por outro lado, se um processo pertence à vista mas não faz parte de , pode ter falhado durante
- Uma aplicação à qual já foi entregue a vista mas à qual ainda não foi entregue a vista diz-se que "está na vista "
- Uma aplicação que usa o modelo de Sincronia na Vista recebe vistas e mensagens
- Se uma aplicação envia uma mensagem quando se encontra na vista , diz-se que foi enviada na vista
- Se uma mensagem é entregue à aplicação depois da vista mas antes da vista , diz-se que foi entregue na vista
- Uma mensagem enviada na vista é entregue na vista
- Se um processo se junta a um grupo e se torna indefinidamente alcançável a partir do processo (sendo ), então eventualmente estará sempre nas views que entrega (a mesma lógica pode ser aplicada a processos que não conseguem comunicar)
Todas estas propriedades culminam nestas duas principais:
-
Comunicação fiável:
- Se um processo correto na vista envia uma mensagem na vista , então é entregue a na vista
- Se um processo entrega uma mensagem na vista todos os processos corretos da vista entregam na vista
-
Corolário:
- Dois processos que entregam as vistas e entregam exactamente o mesmo conjunto de mensagens na vista
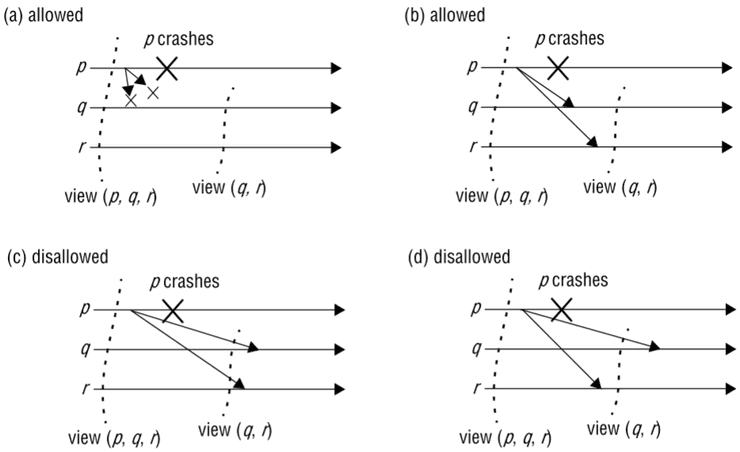
Exemplo
Considere um grupo com três processos, , e . Suponha que envia uma mensagem na view , mas este falha depois de enviar . A seguinte figura ilustra as execuções possíveis:
Para mudar de vista:
- é necessário interromper temporariamente a transmissão de mensagens de forma a que o conjunto de mensagens a entregar seja finito
- é necessário executar um algoritmo de coordenação para garantir que todos os
processos corretos chegam a acordo sobre:
- qual a composição da próxima vista
- qual o conjunto de mensagens a ser entregue antes de mudar de vista
Difusão Atómica
Consiste em ter as garantias de Difusão Fiável + Ordem total:
- Difusão Fiável: se uma réplica recebe o pedido, todas as réplicas recebem o pedido
- Ordem total: todas as réplicas recebem os pedidos pela mesma ordem
A abordagem básica para implementar ordenação total é atribuir identificadores totalmente ordenados às mensagens multicast, de modo a que cada processo tome a mesma decisão de ordenação com base nesses identificadores.
Algoritmos de ordem total (sem falhas):
-
Ordem total baseada em sequenciador:
- as mensagens são enviadas para todas as réplicas usando um algoritmo de Difusão Fiável
- é eleito um líder que decide a ordem pela qual as mensagens devem ser processadas, enviando esta informação para as réplicas restantes
- quando existe uma falha, as réplicas podem ser confrontadas com um estado
incoerente:
- mensagens de dados que não foram ordenadas pelo líder
- mensagens do líder referentes a mensagens que ainda não chegaram
- podem existir de forma geral diferenças nas perspectivas que cada réplica tem do sistema
- Todos estes problemas são resolvidos na camada de Sincronia na Vista
-
Ordem total baseada em acordo coletivo:
- um processo envia uma mensagem multicast para os membros do grupo. Estes processos propõem números de sequência para a mensagem (atribuição "tentativa") e devolvem-nos ao remetente, que gera o número de sequência acordado com base nos números propostos (atribuição final).
- o algoritmo funciona mesmo que cada mensagem seja enviada para um sub-conjunto diferente de nós
- quando há falhas, é preciso executar um algoritmo de reconfiguração que fica
bastante simplificado pela Sincronia na Vista
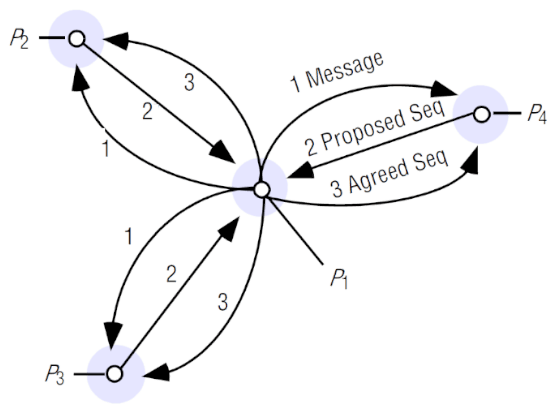
Exemplo de aplicação no algoritmo de Maekawa
Iremos analisar o funcionamento do algoritmo de Skeen (em que o cliente escolhe o maior dos números de sequência propostos) aplicado à exclusão mútua de Maekawa.
Existem três clientes , e , com quóruns , e .
e já receberam o pedido de , marcando-os com o número de sequência 1 e 2 (respectivamente) e enviando essas propostas ao cliente. Estes pedidos encontram-se no estado "tentativo" (T), já que se tratam de propostas, ainda não foram confirmados.
O cliente ao receber estes dois números, escolhe o mais alto (2) e envia essa informação ao seu quórum. O pedido de encontra-se agora ordenado definitivamente (estado final, F).
Ao chegar ao topo da lista de com estado final, é enviado para a camada de aplicação, que neste caso é o algoritmo Maekawa. dá acesso a à exclusão mútua dado estar livre. Entretanto chegou também o pedido de a , que foi marcado com o número 3.
O cliente recebe 1 e 3 como propostas, pelo que escolhe 3. Chega agora o pedido de a , que lhe atribui o número 4.
Os pedidos de chegaram ao topo, pelo que foram enviados para a camada superior. colocou como pendente, pois tem a exclusão mútua, e concedeu-lhe acesso. recebe como respostas 1 e 4, pelo que escolhe 4, o que faz com que vá para o topo da lista de .
O pedido de é enviado para a camada superior e ganha o acesso à exclusão mútua em . Em , é enviado o pedido de , que fica na lista de pendentes dado já existir outro cliente na exclusão mútua. De seguida, o pedido de em passa a estar no topo da lista com estado final, pelo que também é enviado. já está na exclusão mútua, portanto é adicionado à lista de pendentes.
Recordar: O algoritmo de Maekawa tinha uma falha: era suscetível a deadlocks. Ao utilizarmos ordem total, garantindo que todos os processos recebem os pedidos pela mesma ordem, este problema fica resolvido.
Algoritmo Primário-secundário (concretizado)
- Primário usa Difusão Fiável Uniforme síncrona na vista para propagar
novos estados aos secundários
- só responde ao cliente quando a uniformidade estiver garantida
- Réplicas usam Sincronia na Vista para lidar com falhas do primário:
- quando o primário falha, eventualmente será entregue nova vista sem
- quando uma nova vista é entregue e o anterior primário não consta nela, os restantes processos elegem o novo primário
- o novo primário anuncia o seu endereço num serviço de nomes (para que os clientes o descubram)
Replicação de máquina de estados (concretizado)
- Processos usam Sincronia na Vista
- Clientes usam Difusão Atómica síncrona na vista para enviar pedidos a todas as réplicas
Nota
Este tipo de replicação não alcança a linearizabilidade (ao contrário da replicação primário-secundário) porque a ordem total na qual os gestores de réplicas processam os pedidos pode não coincidir com a ordem real na qual os clientes fizeram os pedidos.
Consenso e Replicação
Iremos agora analisar como resolver problemas/algoritmos relacionados com replicação através do consenso.
Difusão atómica usando Consenso
Uma primeira abordagem poderia ser:
- cada processo guarda uma lista de mensagens Recebidas () e Ordenadas ()
- sempre que tiver alguma mensagem recebida que ainda não está ordenada, propõe essa mensagem para consenso (uma instância de consenso por mensagem a ordenar)
- o consenso decide qual a próxima mensagem, que é adicionada à lista de mensagens ordenadas de cada processo
Esta abordagem tem um problema: como o consenso pode decidir qualquer uma das mensagens propostas, é possível que uma mensagem que apenas um processo recebeu nunca seja decidida (e portanto entregue):
A solução é propôr para consenso todas as mensagens recebidas mas não ordenadas (). A decisão do consenso será qualquer um dos sets propostos pelos processos:
Pseudocódigo
Primário-secundário com detector de falhas não perfeito
Já abordámos uma implementação de replicação com Primário-secundário que utilizava Sincronia na Vista e Difusão Fiável, mas será que é possível construir uma solução robusta sem um detector de falhas perfeito?
Utilizaremos o detector não perfeito para escolher o primário:
- devido à natureza do detector, podem existir dois processos que pensam ser o primário
- as réplicas secundárias podem também divergir sobre quem consideram ser o primário
No exemplo acima, o primário decide que a primeira mensagem é e envia essa informação a , que a regista com sucesso. No entanto, a mensagem não chegou a devido a uma partição na rede, que após não receber mensagens do primário durante algum tempo se elegeu como primário, escolhendo como primeira mensagem.
Precisamos agora de um algoritmo que consegue resolver consenso sem um detector de falhas perfeito... O floodset consensus não consegue, já que foi arquitetado exatamente com esse pressuposto. Mas podemos usar o Paxos mencionado anteriormente!
Resumidamente, o Paxos garante que o sistema apenas avança quando tem aprovação da maioria das réplicas. Desta forma, P1 e P2 conseguem continuar a execução normal do algoritmo enquanto que as propostas de P3 (por exemplo, escolher a mensagem E como primeira) não são aceites por uma maioria. Quando a estabilidade da rede voltar ao normal, P3 irá receber as operações que foram realizadas na sua "ausência" e o sistema voltará a estar consistente.
Pseudocódigo
Sincronia na Vista usando Consenso
Mudar da vista para a consiste essencialmente em:
- recolher todas as mensagens entregues durante
- propôr para consenso um tuplo:
- =
- esperar decisão do consenso
- entregar mensagens em falta
- entregar nova vista
Funcionamento do algoritmo:
- cada processo mantém um registo de todas as mensagens que já entregou numa dada vista
- quando se inicia a mudança de vista de para , é enviada uma mensagem especial "" para todos os processos da vista (podendo a lista de saídas e/ou entradas ser vazia)
- quando um processo recebe uma mensagem "", pára de entregar novas mensagens e inicia , para todos os processos na vista e envia para todos os outros processo em
- cada processo recebe os valores de todos os outros processos em
- se um processo não recebe de um processo e suspeita que falhou, remove de e coloca
- quando um processo tem todos os valores de (ou seja, se já recebeu de ou se assume que falhou), define o conjunto de mensagens a entregar como a união de todos os recebidos e inicia o consenso propondo
- o resultado do consenso define a nova vista e o conjunto de mensagens a entregar na vista anterior
Referências
- Coulouris et al - Distributed Systems: Concepts and Design (5th Edition)
- Secções 6.5 e 18.1-18.4
- Departamento de Engenharia Informática - Slides de Sistemas Distribuídos (2023/2024)
- SlidesTagus-Aula05 (informação + imagens)
- SlidesAlameda-Aula05
- SlidesTagus-Aula06
- SlidesAlameda-Aula06
- SlidesTagus-Aula07
- SlidesAlameda-Aula07
- SlidesAlameda-Aula09
- D. B. Terry, A. J. Demers, K. Petersen, M. J. Spreitzer, M. M. Theimer and B. B. Welch, "Session guarantees for weakly consistent replicated data"
- Conflict-free replicated data type, Wikipedia