Segurança e Criptografia

Mecanismos Básicos de Comunicação Segura

Iremos abordar como é possível comunicar com outra entidade de forma segura, garantindo que não existem intrusos a intercetar a conversa, a modificar o conteúdo das mensagens ou a fazer-se passar por um de nós.

Algumas notas prévias:

• Iremos designar por $A$ e $B$ as entidades que pretendem estabelecer um canal seguro (tipicamente designadas por "Alice" e "Bob")
• Uma entidade que queira escutar ou perturbar a comunicação será designada por $T$ (tipicamente designada por "Trudy", de "intruder")

Vamos estudar de seguida mecanismos básicos utilizados para tornar um canal seguro.

Chaves simétricas

No contexto de uso de uma chave simétrica existe:

• uma chave secreta $K_S$ conhecida por $A$ e $B$
• um texto $m$ (plaintext)
• uma função de cifra que produz um texto cifrado (ciphertext) a partir de $m$ e $K_S$, designada $K_S(m)$
  • NOTA: a chave em si não cifra a mensagem, esta é utilizada por um algoritmo
• uma função para decifrar o texto cifrado que usa a mesma chave: $m = K_S(K_S(m))$

Podemos nestas condições criar um canal seguro entre $A$ e $B$ desde que estes conheçam previamente a chave, mas como é que a distribuição da chave é feita? Por exemplo, pode ser trocada fisicamente ou então derivada de uma palavra chave combinada previamente.

Existem dois grandes problemas com o uso desta chave:

• Como podemos ter a certeza de que estamos de facto a ler o que foi enviado pela outra entidade?
• Um intruso $T$ pode simplesmente escutar o que $A$ envia para $B$ e reenviar exatamente a mesma mensagem a $B$ (fazendo com que $B$ execute uma transferência bancária duas vezes por exemplo)

Chaves assimétricas

Agora em vez de termos apenas uma chave partilhada, cada entidade passa a possuir um par de chaves ($K_+$, $K_-$), designadas por chave pública e privada, respectivamente. Estas chaves apresentam as seguintes propriedades:

• a chave pública $K_+$ é partilhada com as outras entidades
• a chave privada $K_-$ é mantida secreta
• $K_+(K_-(m)) = m$
• $K_-(K_+(m)) = m$
• não é possível obter uma chave a partir da outra

A utilização destas chaves permite que, ao enviarmos uma mensagem para $B$, se a encriptarmos com a chave $K_{B+}$, somente $B$, com a sua chave privada $K_{B-}$, será capaz de decifrá-la. Para além disso, se $A$ desejar provar a $B$ que o texto $m$ foi produzido por si, basta encriptar $m$ com $K_{A-}$ e $B$ decifrar com $K_{A+}$. Se for bem sucedido, então $m$ foi garantidamente enviado por $A$, já que apenas este conhece $K_{A-}$.

O uso destas chaves tem no entanto uma grande desvantagem: a criptografia assimétrica é muito mais lenta do que a simétrica (100 a 1000 vezes). Por este motivo, é muito comum utilizar esta criptografia para negociar uma chave simétrica durante a criação do canal seguro (de forma a garantir que estamos a comunicar com a entidade certa), que será posteriormente utilizada na encriptação de toda a comunicação (método conhecido como "chave mista"). Exemplo:

1. $A$ cria uma chave simétrica $K_S$ e cifra-a com $K_{B+}$
2. Apenas $B$ consegue obter $K_S$ já que é o único que possui $K_{B-}$

Funções de Hash Criptográficas

De forma a conseguirmos ter a garantia que estamos a ler o que foi enviado pelo remetente, podemos utilizar uma função de hash e enviar o hash do texto (também conhecido como "digest") juntamente com o mesmo.

Dado um texto $m$, uma função de hash criptográfica cria um hash de tamanho fixo $H(m)$. Estas funções apresentam uma propriedade fundamental que é ser computacionalmente inviável encontrar em tempo útil outro texto $m'$ tal que $H(m') = H(m)$, ou seja, em termos práticos é impossível modificar o texto de forma a que tenha o mesmo hash que o original.

Para aumentar ainda mais a segurança do hash, podemos calculá-lo a partir do texto e da chave privada (simétrica), em vez de apenas do texto.

Nonce

Um nonce é uma palavra chave única que é utilizada para identificar uma troca de mensagens e que não é usada novamente em comunicações posteriores.

O objetivo da utilização do nonce é eliminar uma vulnerabilidade mencionada anteriormente: um atacante pode simplesmente repetir as mensagens cifradas (problema conhecido como "replay attack"). Ao utilizar uma palavra chave única por comunicação, caso um atacante repita as mensagens posteriormente, estas serão ignoradas pelo destinatário, pois este sabe que se tratam de mensagens repetidas.

O cálculo de um nonce é tipicamente baseado numa das seguintes técnicas (ou na sua combinação):

• timestamps (segurança dependente da segurança do relógio da máquina)
• números de sequência monotonicamente crescentes (segurança dependente da capacidade das máquinas memorizarem o último número usado)

Os nonces também podem ser utilizados para garantir que estamos a falar com a entidade certa:

• encriptamos o nonce com uma chave
• esperamos que a outra entidade devolva uma versão modificada (determinista) do nonce enviado (por exemplo, nonce + 1)
• como apenas a outra entidade detém a chave de forma a decifrar o que enviamos, apenas esta consegue ler o nonce enviado e modificá-lo como combinado

Mecanismos Avançados de Comunicação Segura

Combinando todos os mecanismos abordados até agora, podemos obter outros mais sofisticados, como por exemplo:

• Assinaturas digitais
• Infra-estruturas de chaves públicas e certificados
• Troca segura de e-mails
• Canais seguros
• Sistemas de autenticação com "single sign-on"

Assinaturas Digitais com Chave Simétrica

$A$ e $B$ partilham uma chave $K_S$ e $A$ quer assinar um texto $m$ de forma a que $B$ possa confirmar que $m$ foi gerado por $A$ (autenticidade) e que não foi alterado durante o percurso (integridade). Para tal:

• $A$ cria uma versão estendida do texto ($m|K_S$), concatenando ao texto $m$ o segredo $K_S$
• $A$ usa uma função de hash criptográfica para gerar o digest da versão estendida $S_m = H(m|K_S)$
• $A$ envia ambos a $B$
• $B$ verifica se $S_m = H(m|K_S)$

Este tipo de assinatura apenas pode ser usado entre duas entidades que partilham um segredo e é tipicamente designado por Message Authentication Code (MAC)

Assinaturas Digitais com Chave Assimétrica

$A$ tem $K_{A-}$ e $B$ conhece $K_{A+}$ (veremos como é que isto é possível com certificados). $A$ quer assinar um texto $m$ de forma a que $B$ possa confirmar a sua autenticidade e integridade, e que também consiga provar a outro que a mensagem $m$ foi de facto enviada por $A$ (não repúdio). Para tal:

• $A$ usa uma função de hash criptográfica para gerar o digest da mensagem $H(m)$
• $A$ usa a sua chave privada $K_{A-}$ para cifrar $H(m)$
• $K_{A-}(H(m))$ serve como assinatura de $m$
• qualquer entidade pode usar a chave pública $K_{A+}$ para validar a assinatura

Infra-estruturas de chaves públicas e certificados

Quando falámos de chaves assimétricas, vimos que corriamos um perigo ao tentar descobrir a chave pública da outra entidade: estávamos suscetíveis ao Men-in-the-middle attack. Esta vulnerabilidade existe já que não conseguimos ter a certeza de que estamos de facto a falar com a entidade pretendida, nem de verificar a autenticidade da chave pública que nos é devolvida.

Há duas formas de evitar este problema:

• se soubermos de antemão a chave pública de $B$, enviamos-lhe a chave simétrica cifrada com a sua chave pública (assim um intruso não consegue obter a nossa chave e fazer-se passar por $B$)
• se existir um certificado digital que confirma que a chave que recebemos é de facto a de $B$, $B$ pode enviar-nos o certificado

As autoridades que emitem estes certificados denominam-se Certification Authorities (CA). Assume-se que a chave pública das CA's é previamente conhecida (normalmente os browsers trazem os certificados associados às CA's pré-instalados).

Um certificado digital consiste num documento que associa uma entidade a uma chave pública e que está assinado pela CA.

Após verificarmos que o certificado recebido está assinado pela CA, ainda precisamos de garantir que a entidade com a qual estamos a contactar é de facto legítima antes de negociarmos uma chave simétrica para usar durante a sessão, e para tal podemos usar a estratégia mencionada previamente que utiliza um nonce:

• ciframos um nonce com a chave pública retirada do certificado
• esperamos receber uma versão modificada do mesmo

Por vezes, existe a necessidade de invalidar um certo certificado. Seria caro, se não impossível, rastrear e apagar todas as cópias locais do certificado. A solução mais comum para este problema é incluir uma data de validade no próprio certificado, sendo que a receção de certificados expirados deve ser rejeitada (o titular do certificado deve solicitar a renovação do mesmo).

Troca segura de e-mails

Um exemplo de sistema seguro de troca de e-mails é o PGP, Pretty Good Privacy:

• cada utilizador possui um par de chaves simétricas
• divulga a sua chave pública de forma a que outros possam ter acesso e confiança de que lhe pertence
• para garantir que um e-mail não é alterado:
  • gera uma assinatura criptográfica do conteúdo e assina-a com a sua chave privada
  • o destinatário pode obter o digest original e confrontá-lo com o que é gerado pelo conteúdo que recebeu
• para garantir que apenas o destinatário lê o e-mail:
  • cria uma chave simétrica para cifrar o conteúdo do e-mail
  • cifra essa chave com a chave pública do destinatário
  • envia o conteúdo cifrado juntamente com a chave simétrica cifrada
  • como o destinatário é o único que possui a sua chave privada, apenas este consegue obter a chave simétrica para decifrar o conteúdo do e-mail

Canais seguros (SSL/TLS)

Seja $A$ um browser e $B$ um servidor WWW que pretendem criar um canal seguro. Para tal, podem usar TLS (Transport Layer Security) ou SSL (Secure Sockets Layer, substituído pelo TLS).

Iremos apresentar de uma forma simplificada o funcionamento do protocolo SSL:

• $A$ envia um pedido a $B$ solicitando a sua chave pública, juntamente com um nonce, que será usado para tornar a ligação única
• $B$ devolve um certificado com a sua chave pública, juntamente com outro nonce
• $A$ verifica a validade do certificado, abortando a ligação caso falhe
• $A$ utiliza o nonce recebido para gerar um segredo (designado por "master secret") que irá partilhar com $B$
• $A$ cifra o segredo com a chave pública de $B$ e envia-lho
• $B$ fica a conhecer também o "master secret"
• $A$ e $B$ criam de forma determinista um conjunto de chaves simétricas que usam para concretizar o canal seguro
  • estas chaves são geradas a partir do "master secret" e dos nonces trocados
  • são criadas 4 chaves:
    • $K_C =$ chave usada para cifrar os dados enviados do cliente para o servidor
    • $M_C =$ chave para assinar, com um MAC, os dados enviados do cliente para o servidor
    • $K_S =$ chave usada para cifrar os dados enviados do servidor para o cliente
    • $M_S =$ chave para assinar, com um MAC, os dados enviados do servidor para o cliente
• os dados trocados no canal são agrupados em blocos designados por "records"
• cada record é marcado com um campo que designa o seu tipo
  • existe um tipo de record específico para fechar a ligação
• cada record é assinado pelo emissor com um MAC
  • para gerar o MAC de um record, o emissor usa a sua chave $M$, o tipo do block e um número de sequência
  • MAC $= \text{Hash(record||M||type||sequence\_number)}$
  • impedindo assim que um record seja alterado ou reordenado dentro de uma sequência sem que isso seja detetado
• os records são ainda cifrados antes de serem enviados, para assegurar a confidencialidade

Autenticação

Já sabemos como podemos estabelecer canais seguros, garantindo a $A$ que está realmente a comunicar com $B$, mas e caso $B$ queira saber a identidade de $A$? Quando um cliente se conecta a uma página web de acesso livre, o servidor não precisa de saber quem $A$ é, mas isto já não é verdade caso tenha funcionalidades privadas (para saber se pode fornecer o serviço).

Uma solução poderia passar por $A$ possuir um par de chaves assimétricas, estando a chave pública assinada por uma CA. Mas como $A$ seria por norma uma pessoa, a solução torna-se pouco prática, já que esta teria de manter o seu certificado com a sua chave pública em todos os seus dispositivos (para além de ter que proteger o certificado para impedir a utilização indevida em caso de roubo).

Geralmente a autenticação é feita através de um segredo que é partilhado entre $A$ e $B$ (como uma palavra-passe), e que é utilizado para estabelecer o canal seguro. Este tipo de autenticação pode ser usado em sistemas que usam canais seguros baseados tanto em chaves simétricas como assimétricas.

Autenticação com Chaves Simétricas

• O cliente e o servidor partilham um segredo (tipicamente a palavra-passe do cliente) a partir do qual é possível derivar uma chave simétrica $K_A$
• Para estabelecer um canal, o cliente $A$ envia para o servidor $B$ o tuplo $\text{<A, nonce>}$
• O servidor gera uma chave simétrica única $K$ que será usada para estabelecer a comunicação segura e envia-a ao cliente num tuplo cifrado com a chave simétrica partilhada $K_A(\text{<nonce, K>})$
• Apenas $A$ pode extrair $K$, já que $K_A$ vem da sua password
• Quando $A$ usar $K$, prova a sua identidade

Autenticação com Chaves Assimétricas

• O cliente $A$ estabelece um canal seguro com o servidor $B$ usando um protocolo baseado em chaves assimétricas, semelhante ao SSL/TLS descrito de forma breve anteriormente
• O cliente usa o canal seguro para enviar as suas credenciais
  • palavra-passe
  • possivelmente outros mecanismos de autenticação adicionais, tais como códigos recebidos por e-mail ou SMS

Autenticação em Múltiplos Serviços

Ambos os protocolos mencionados anteriormente obrigam o cliente a partilhar um segredo (palavra-passe) com cada servidor e a repetir todo o processo de autenticação sempre que quer aceder a um novo serviço. Isto apresenta desvantagens: além de obrigar o cliente a manter várias palavras-passe, torna-se pouco prático e repetitivo quando se quer usar vários serviços dentro de uma mesma organização (Webmail IST, Fénix, Moodle).

Uma solução que não apresenta estes "problemas" é recorrermos a um servidor central de autenticação, no qual tanto os clientes como os servidores confiam:

• o servidor auxilia o cliente no estabelecimento de um canal seguro entre este e os servidores, sem necessitar de repetir o processo de autenticação
• o cliente passa a apenas ter que partilhar segredos com o servidor de autenticação
• os serviços também apenas partilham segredos com este servidor
• pode ser feito com chaves simétricas ou assimétricas

Protocolo de Needham-Schroeder

O protocolo de autenticação de Needham-Schroeder funciona da seguinte forma:

1. $A \rarr S: A, B, N_A$
   • em que $N_A$ é um nonce
   • $A$ pede a $S$ uma chave para comunicar com $B$
2. $S \rarr A: \Set{N_A, B, K_{AB}, \Set{K_{AB}, A}_{K_B}}_{K_A}$
   • $S$ devolve uma mensagem cifrada com a chave de A $K_A$ (obtida através do segredo partilhado: palavra-passe) com os seguintes elementos:
     • a chave gerada para $A$ comunicar com $B$, $K_{AB}$
     • o nonce $N_A$ para demonstrar que a mensagem foi enviada em resposta ao pedido de $A$
     • um "ticket" cifrado com a chave de $B$ $K_B$: $\Set{K_{AB}, A}_{K_B}$, que será entregue por $A$ a $B$ na primeira comunicação, servindo de prova a $B$ que $A$ está autenticado e se trata de facto de $A$
   • como a mensagem vem cifrada com a chave de $A$ $K_A$, este confia que foi mesmo $S$ que a enviou, já que apenas este sabe o seu segredo (além de si próprio)
3. $A \rarr B: \Set{K_{AB}, A}_{K_B}$
   • $A$ envia o ticket a $B$
4. $B \rarr A: \Set{N_B}_{K_{AB}}$
   • $B$ decifra o ticket e usa a nova chave $K_{AB}$ para cifrar um novo nonce, $N_B$
5. $A \rarr B: \Set{N_B - 1}_{K_{AB}}$
   • $A$ demonstra a $B$ que foi de facto ele quem enviou o ticket ao devolver uma versão modificada de $N_B$

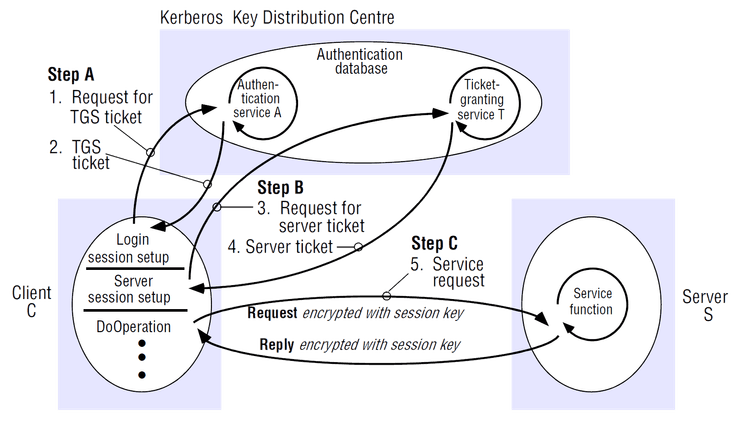
Sistema de Autenticação Kerberos

Consiste num sistema de autenticação baseado no protocolo de Needham-Schroeder que se tornou um "internet standard". Permite efetuar o que se designa por "single sign-on":

• o utilizador apenas utiliza as suas credenciais para estabelecer um canal seguro com o servidor de autenticação
• daí para a frente usa esse canal seguro para obter chaves simétricas para aceder a outros serviços

Single sign-on com Chaves Assimétricas

Pode-se aplicar o mesmo princípio utilizado no Needham-Schroeder /Kerberos em sistemas com chaves assimétricas. É algo bastante usado hoje em dia por exemplo quando fazemos login num serviço usando a conta Google.

O funcionamento resume-se ao seguinte:

1. o cliente $A$ cria um canal seguro com o servidor $B$ (usando SSL por exemplo)
2. o servidor $B$ permite que a verificação da identidade de $A$ seja feita por um fornecedor de identidades (FI) externo em quem ambos confiam
3. $B$ envia a $A$ um token cifrado com a chave pública de FI $\text{FI}_+$ que contém informação sobre o cliente de forma a que o FI consiga concluir o processo de autenticação
4. $A$ contacta o FI usando a sua palavra-passe (apenas partilhada com FI), entregando-lhe o token
5. o FI confirma a identidade de $A$ e que possui uma relação de confiança com o serviço $B$
6. o FI gera um token de acesso cifrado com a chave pública de $B$ $K_{B+}$ que o cliente $A$ pode fornecer a $B$ como prova de que foi autenticado pelo FI
7. $A$ entrega o token a $B$ e conclui assim o processo de autenticação

Nota: os tokens trocados entre $B$ e FI são cifrados com as respectivas chaves públicas para que o cliente não os consiga alterar.

Referências

• Coulouris et al - Distributed Systems: Concepts and Design (5th Edition)
  • Secções 11.1-11.2 e 11.4-11.6
• Departamento de Engenharia Informática - Slides de Sistemas Distribuídos (2023/2024)
  • SlidesTagus-Aula11
  • SlidesAlameda-Aula12