Tempo e Sincronização
Tempo
Num sistema centralizado não existe ambiguidade quanto ao tempo. Quando um processo A pretende saber o tempo atual, pode consultar o relógio do sistema. Se momentos mais tarde o processo B obtiver o tempo, este será superior (ou possivelmente igual) ao tempo obtido pelo processo A.
Num sistema distribuído o problema é mais complexo. Não existe tempo global, cada computador tem o seu próprio relógio e o tempo que estes relógios indicam pode ser diferente.
Relógios Físicos
Praticamente todos os computadores têm um circuito para contar o tempo, baseados num cristal de quartzo. Este cristal oscila a uma frequência conhecida, e o circuito conta o número de oscilações, podendo assim determinar o tempo. Ao fim de um determinado número de oscilações, o circuito gera uma interrupção a que se chama tick de relógio.
Como qualquer outra medição, existe uma incerteza associada à frequência do cristal, e por isso a frequência de ticks de relógio pode variar entre relógios. Mesmo para o mesmo relógio, a frequência pode variar com fatores externos como a temperatura. A variação é normalmente pequena, mas o erro acumulado pode levar a que dois relógios apresentem uma diferença significativa no tempo que contam.
Tempo Universal Coordenado (UTC)
Dada esta incerteza, surge a necessidade de um tempo universal, que sirva de referência para todos os relógios. Para tal, o International Time Bureau (BIH) recolhe medições de 450 relógios atómicos (capazes de uma precisão extremamente superior à dos relógios de quartzo) em 80 laboratórios distintos e calcula o tempo médio. Esta medição é o Tempo Atómico Internacional (TAI).
Por mais preciso que o TAI seja, não tem em conta o desvio da hora solar, pelo que um segundo standard foi criado, baseado no TAI mas incluindo leap seconds, o Tempo Universal Coordenado (UTC). Vários satélites transmitem UTC, sendo possível obter precisões na ordem dos nanosegundos.
Métricas de Desempenho de Relógios
Com uma referência externa, pode-se definir métricas para avaliar o desempenho de relógios. Para as definir, temos que é o tempo UTC e é o tempo contado pelo relógio no instante .
O skew é a diferença entre o tempo contado por dois relógios, ou seja:
A deriva do relógio é a taxa a que um dado relógio se afasta do tempo de referência:
Para um relógio perfeito, . Por norma, fabricantes de relógios garantem um desvio máximo. Ou seja, para um desvio máximo :
Diz-se que um relógio está correto quando o seu drift rate respeita a especificação do fabricante. Esta condição impede saltos no tempo, porém, tal nem sempre é desejável. Uma condição mais flexível é a de monotonia, que impede que o relógio retroceda no tempo:
Nota
Garantir a monotonia de um relógio é fundamental para o correto funcionamento de programas que se baseiam no tempo. Por exemplo, a ferramenta make do UNIX é utilizada para compilar apenas os ficheiros que foram modificados desde a última compilação. Se o tempo retroceder entre compilações, a ferramenta não funciona como desejado.
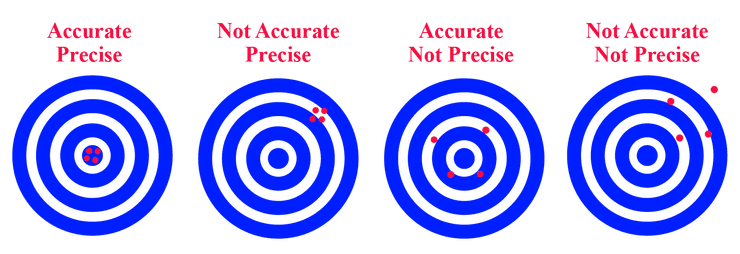
Para conjuntos de relógios, pode-se ainda falar de precisão e exatidão.
A precisão é a medida da dispersão das medições dos vários relógios. Para uma precisão , temos que a diferença entre quaisquer dois relógios nunca excede , ou seja:
Por outro lado, a exatidão é a medida da diferença do conjunto de relógios com uma referência externa. Para uma exatidão , temos que a diferença entre qualquer relógio e o tempo de referência nunca excede , ou seja:
Sincronização de Relógios Físicos
Num sistema distribuído em que uma das máquinas está instalada com um recetor de UTC, pode-se usar este relógio como referência para sincronizar os outros. Trata-se de sincronização externa, em que é usada uma referência externa para obter exatidão e precisão no sistema.
Porém, a exatidão nem sempre é relevante, sendo mais importante a precisão para que todos os nós do sistema concordem sobre o tempo. Nestes casos usa-se sincronização interna, em que os relógios são sincronizados entre si.
Algoritmo de Cristian
O Algoritmo de Cristian é um algoritmo de sincronização externa que usa um servidor de tempo.
O processo envia uma mensagem ao servidor de tempo e espera pela resposta , que inclui , com sendo o momento em que a resposta sai de .
O processo não pode usar o tempo incluído na mensagem , pois estaria a desprezar o tempo de transmissão. Assim, mede o e, assumindo que o tempo de transmissão de para é igual ao de para , estima o tempo atual como:
Caso o ajuste de tempo requira um avanço no tempo, ocorre diretamente. No entanto, se for necessário um retrocesso, de modo a não se violar a monotonia com um salto para trás, a frequência de clock ticks é reduzida, até o tempo estimado ser alcançado.
É importanto notar que não é garantido simetria no tempo de transmissão, pelo que a estimativa do tempo tem alguma incerteza. No pior caso, em que uma das mensagens é enviada instantaneamente mas a resposta demora , o tempo estimado estará errado por . A precisão deste algoritmo é, portanto, .
Pode-se melhorar a precisão caso se conheça o tempo mínimo de transmissão, ficando .
Este algoritmo é simples, no entanto, tem um único ponto de falha. Se o servidor de tempo falhar, o sistema não consegue sincronizar os relógios. Cristian propõe que o pedido seja feito em multicast a vários servidores de tempo, selecionando o que responder primeiro, resultando na melhor precisão.
Exercício
Um cliente pretende sincronizar-se com um servidor e para tal regista o RTT e os tempos enviados pelo servidor:
| RTT (ms) | Time (hh:mm:ss) |
|---|---|
| 22 | 10:54:23.674 |
| 25 | 10:54:25.450 |
| 20 | 10:54:28.342 |
1. Com qual dos valores deve o servidor se sincronizar de modo a obter a melhor precisão?
R: Com o terceiro (10:54:28.342), pois apresenta o menor RTT ()
2. Qual o valor do relógio após o acerto?
R: 10:54:28.342 10:54:28.352
3. Qual a precisão do acerto?
R:
4. E se soubermos que o tempo de envio de uma mensagem é no mínimo de 8ms, essa precisão é alterada? Se sim, qual o novo valor?
R:
Algoritmo de Berkeley
O Algoritmo de Berkeley é um algoritmo de sincronização interna. Por simplicidade, o exemplo será dado para um sistema com 3 processos, o processo coordenador e os processos e , mas o algoritmo pode ser estendido a qualquer número de processos.
Neste algoritmo, é eleito um coordenador , responsável por periodicamente enviar pedidos a todos os outros processos, que devem responder com o seu tempo.
O coordenador recebe as respostas e e calcula a média dos tempos, incluindo o próprio:
O coordenador calcula a diferença entre o tempo médio e o tempo de cada processo e envia a diferença para que os processos ajustem o seu relógio. As diferenças podem ser positivas ou negativas e são calculadas da seguinte forma:
Cada processo ajusta o seu relógio, de acordo com a diferença recebida.
O algoritmo apresentado foi simplificado, na versão real é tido em conta o tempo de transmissão, da forma como foi feito no Algoritmo de Cristian. É ainda definido um valor máximo para o RTT (dependendo da exatidão desejada), permitindo ao coordenador eliminar ocasionais leituras que ultrapassem esse valor.
Em caso de falha do coordenador, um novo coordenador é eleito. Falar-se-á de eleições na próxima publicação.
Exercício
Existem 3 máquinas A, B e C, sendo o master A. A enviou a sua hora (13:15:15)
a todos e recebeu as seguintes respostas:
| Time (hh:mm:ss) |
|---|
| [ A = 13:15:15 ] |
| B = 13:15:05 |
| C = 13:16:07 |
Qual é o acerto enviado pelo master a cada máquina?
Network Time Protocol (NTP)
Tanto o Algoritmo de Cristian como o Algoritmo de Berkeley são algoritmos desenhados para operar em intranets. O NTP define um protocolo para distribuir informação de tempo através da Internet.
Os objetivos de desenho do NTP são:
- Prestar um serviço que permita que os clientes na Internet sejam sincronizados com precisão com o UTC.
- Prestar um serviço confiável que possa sobreviver a longos períodos de perda de conectividade.
- Permitir que os clientes se resincronizem com frequência suficiente para compensar as taxas de desvio encontradas na maioria dos computadores.
- Proteger contra interferências com o serviço de tempo, quer sejam intencionais ou acidentais.
O protocolo NTP baseia-se no Algoritmo de Cristian, mas em vez apenas medir o , registam-se os valores reportados por para o envio de e recepção de , e , e os valores reportados por para a recepção de e envio de , e . Desta forma, o tempo entre a chegada de uma mensagem e o envio da próxima não é contabilizado.
Calcula-se a diferença entre os tempos reportados entre o envio e recepção de cada mensagem:
Podemos, por fim, calcular a diferença dos deltas para obter o offset e a média para obter o delay :
O offset é uma estimativa do com incerteza de . Quanto menor o delay, melhor a estimativa. O algoritmo armazena os últimos 8 pares , escolhendo de entre estes o par com o menor de forma a obter o mais preciso. Este valor é então usado para ajustar o relógio de :
O protocolo NTP pode funcionar em 3 modos:
- Multicast: O procedimento descrito anteriormente não se aplica e simplesmente é enviado o tempo atual em multicast para todos os clientes. Só se deve usar este modo em LANs de alta velocidade.
- Chamada a procedimento: O protocolo decorre de acordo com o descrito anteriormente.
- Simétrico: O protocolo decorre de acordo com o descrito anteriormente, mas a sincronização é feita em ambos os sentidos.
Aplicar NTP de forma simétrica implica que não só afeta o relógio de , como também afeta o relógio de . Isto pode causar problemas, caso um dos relógios seja mais exato que o outro. Para resolver este problema, o NTP divide as máquinas em níveis (ou strata):
- Uma máquina de nível 1 é um servidor com um relógio de referência, como é o caso de um computador instalado com um receptor de UTC.
- Uma máquina de nível 2 sincroniza com uma máquina de nível 1.
- Uma máquina de nível 3 sincroniza com uma máquina de nível 2, etc...
Uma máquina só ajusta o seu relógio com uma máquina de nível inferior.
Eventos e Relógios Lógicos
Nem sempre é necessário contar o tempo de forma exata. Se dois processos não interagem, a falta de sincronização não pode ser observada, pelo que não poderá causar problemas. Para além disso, em muitos casos, o que realmente é relevante é a ordem em que eventos ocorrem e não o tempo absoluto.
Trata-se de um evento qualquer operação que transforma o estado do processo. Para além de alterações de estado, a recepção e o envio de qualquer mensagem também são eventos.
Num só processo , é trivial determinar a ordem em que eventos ocorrem. Diz-se que antecede no processo se é obsevado por antes de . Esta relação pode ser representada por .
Em sistemas distribuídos, expande-se a definição de happens-before para incluir transmissões de mensagens. Diz-se que antecede se antecede em algum processo ou se correspondem ao envio e recepção de uma mesma mensagem. Para além disso, antecedência é transitiva.
- HB1: Se , então .
- HB2: Se , então .
- HB3: Se , então .
Com estas definições, observa-se que para uma sequência de eventos , se for possível aplicar HB1 ou HB2 a qualquer par de eventos , então, por HB3, .
Nem todos os eventos têm uma ordem de antecedência definida. Diz-se que eventos distintos , são concorrentes sse . Esta relação é representada por . Nada se pode dizer (nem necessita ser dito) sobre a ordem em que estes eventos ocorrem.
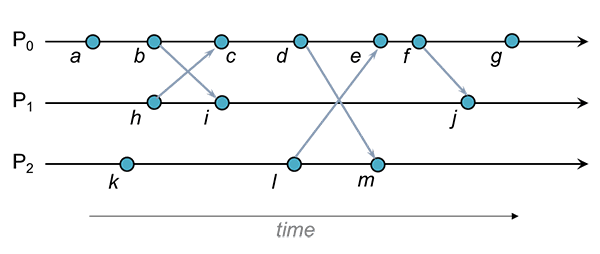
Exemplo
Algumas relações de antecedência encontradas no diagrama:
Algumas relações de concorrência encontradas no diagrama:
Nota
Se dois eventos têm uma relação happened-before, então o primeiro pode ou não ter causado o segundo. Esta relação apenas sugere potenciais causalidades, podendo não haver qualquer ligação entre os eventos (eventos independentes).
Relógio Lógico de Lamport
Leslie Lamport propôs um algoritmo simples para capturar a ordem de eventos num sistema distribuído. Cada processo mantém um relógio lógico monótono que pode ser usado para atribuir uma estampilha temporal a cada evento . Quando o processo em que se atribuiu a estampilha não é relevante, usa-se .
Os relógios são atualizados de acordo com as seguintes regras:
- LC1: é incrementado sempre que um evento é observado por .
- LC2: Quando envia uma mensagem , inclui na mensagem a estampilha com o valor de após executar LC1.
- LC3: Quando recebe uma mensagem , atualiza tal que e depois executa LC1.
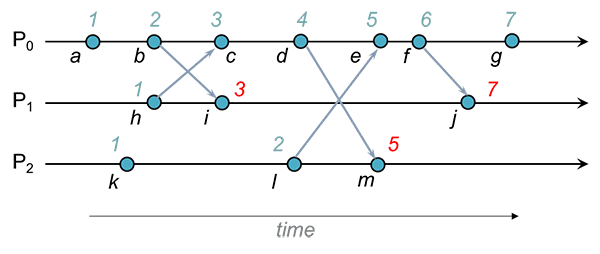
Exemplo
, e mantêm, respetivamente, os relógios , e .
Quando envia a mensagem inclui na mensagem. Quando recebe a mensagem, compara com a estampilha recebida:
Quando envia a mensagem inclui na mensagem. Quando recebe a mensagem, compara com a estampilha recebida:
Relógios lógicos de Lamport garantem a seguinte propriedade:
No entanto, o inverso não é verdadeiro. Isto é, . Pode-se encontrar um caso destes no exemplo anterior: , mas .
Demonstração:
Hipótese de indução: Se , então
Passo base (HB1): Se e ocorrem no mesmo processo, é imediato por LC1 que
Passo base (HB2): Se existe uma mensagem tal que é o evento de envio e é o evento de receção, então por LC2 e LC3
Passo indutivo (HB3): Se e , então e , por HI
Vector Clocks
Para superar esta limitação, Mattern e Fridge desenvolveram o Vector Clock: uma alternativa em que garante também a implicação no sentido contrário.
O Vector Clock é um tuplo de inteiros, um para cada processo participante no sistema distribuído. À semelhança do relógio de Lamport, cada processo mantém um vector clock que pode ser usado para atribuir uma estampilha temporal a cada evento . Quando o processo em que se atribuiu a estampilha não é relevante, usa-se .
- VC1: Inicialmente, para todo o .
- VC2: é incrementado sempre que um evento é observado por .
- VC3: Quando envia uma mensagem , inclui na mensagem a estampilha com o valor de após executar VC2.
- VC4: Quando recebe uma mensagem , atualiza realizando um merge com e depois executa VC2.
A operação de merge dos vector clock e consiste em atualizar cada campo do vector clock tal que , para todo o .
Uma possível intuição para estes valores é a seguinte:
- é o número de eventos que estampilhou.
- () é o número de eventos que já sabe que estampilhou.
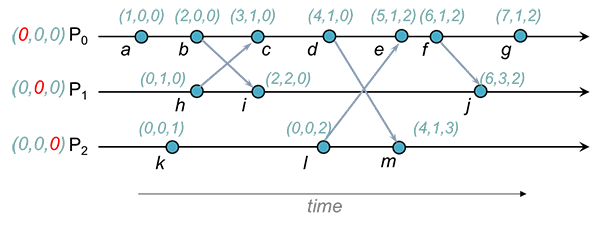
Exemplo
, e mantêm, respetivamente, os relógios , e .
Quando envia a mensagem inclui na mensagem. Quando recebe a mensagem, faz merge de com a estampilha recebida:
Ou seja, .
Quando envia a mensagem inclui na mensagem. Quando recebe a mensagem, faz merge de com a estampilha recebida:
Ou seja, .
Pode-se comparar vector clocks da seguinte forma:
- , para todo o .
- , para todo o .
Ou seja, temos que um vector clock é menor quando nenhum dos seus valores é maior, mas não são iguais. Comparando deste modo, obtemos a seguinte propriedade (uma versão da propriedade do relógio de Lamport mas com equivalência):
Demonstração:
Começamos por mostrar que
Hipótese de indução: Se , então
Passo base (HB1): Se e ocorrem no mesmo processo, é imediato por VC2 que
Passo base (HB2): Se existe uma mensagem tal que é o evento de envio e é o evento de receção, então por VC3 e VC4
Passo indutivo (HB3): Se e , então e , por HI
De seguida, mostra-se que
Para isto, prova-se que para um par de eventos e :
Seja e um par de eventos concorrentes tal que ocorre em e ocorre em . Como os eventos são concorrentes, sabemos que nenhuma mensagem de durante ou após o evento propagou a sua estampilha para pelo momento em que ocorre , e vice versa.
Como ocorreu em e ainda não foi "informado", é garantido que . Temos também que . Provando-se assim o lema e o seu contra-recíproco:
Se dois eventos não são concorrentes, então tem de existir uma relação de happens-before, é evidente que é falso.
Logo, e temos que:
Nota
Em comparação com os timestamps de Lamport, os vector timestamps têm a desvantagem de precisar de uma maior capacidade de armazenamento e transmissão de mensagens, proporcional ao número de processos. No entanto, existem técnicas para armazenar e transmitir quantidades menores de dados, com o custo adicional de processamento para reconstruir os vetores.
Salvaguarda distribuída
Criar uma salvaguarda distribuída (ou distributed snapshot) consiste essencialmente em capturar o estado global do sistema num determinado instante, o que pode ser útil porque permite:
- recuperar o sistema em caso de falha (rollback)
- analisar o sistema de forma a verificar certas propriedades
- depurar o sistema de forma geral
Guardar o estado de todo o sistema de forma coerente é um grande desafio, já que não existe o conceito de "tempo global" (os relógios não estão sincronizados) e o estado das aplicações consiste não só no estado dos seus processos, mas também nas mensagens em trânsito.
Abordagem ingénua
A primeira abordagem que nos pode surgir é existir um coordenador central que pode ordenar aos processos que:
- Parem por completo o que estão a fazer
- Criem um snapshot do seu estado atual
- Esperem por uma notificação do coordenador para retomar atividade (quando o estado de todo o sistema estiver capturado)
O problema óbvio desta abordagem é que parar todo o sistema é ineficiente, pelo que iremos procurar guardar o estado do sistema sem o parar.
Corte coerente
Antes de falarmos de algoritmos que não precisam de parar o sistema, é preciso definir a noção de corte coerente:
Corte coerente
Um corte é coerente se, para cada evento que este contém, também inclui todos os eventos que aconteceram-antes desse evento.
Um evento corresponde a uma ação interna do processo ou ao envio/receção de uma mensagem nos canais de comunicação. Note que o estado destes canais é relevante: se descobrirmos que o processo registou o envio de uma mensagem para o processo , então, examinando se recebeu , podemos inferir se faz ou não parte do estado do canal entre e .
O corte mais à direita é incoerente porque incluiu a receção de mas não incluiu o envio desta mensagem, ou seja, este corte apresenta um "efeito" sem uma "causa". É fácil perceber que a execução real do sistema nunca esteve neste estado, visto que é impossível receber uma mensagem que não foi enviada.
Em contraste, o corte do meio inclui o envio de mas não inclui a receção desta mensagem. Ainda assim, este corte é coerente com a execução real do sistema visto que as mensagens demoram algum tempo a chegar ao destinatário.
Por fim, o corte mais à esquerda é fortemente coerente porque todas as causalidades estão representadas nos estados locais dos processos (não existem mensagens em trânsito).
Algoritmo simples
Consideremos um algoritmo em que:
- qualquer processo pode a qualquer momento iniciar uma salvaguarda global, guardando o seu estado local
- quando o processo acaba de guardar o seu estado:
- envia um marker a todos os outros processos e de seguida prossegue com a sua execução normal
- quando o processo recebe um marker:
- se ainda não guardou o seu estado local, guarda-o
Exercício
Inicialmente, cada processo possui os tokens indicados na imagem. Sabendo que cada mensagem transfere 100 tokens entre 2 processos, qual vai ser o estado capturado pelo algoritmo considerando que P1 inicia um snapshot no instante X?
R:
Justificação:
- P1: Enviou 2 mensagens, pelo que perdeu tokens
- P2: Não enviou nem recebeu mensagens, pelo que o número de tokens não se altera
- P3: Recebeu 2 mensagem de P1 e enviou 1 de volta, pelo que ganhou tokens
IMPORTANTE: A soma de tokens no início era 2000 mas no snapshot é 1900! Não se sabe que mensagens estão em trânsito...
Este algoritmo apresenta uma falha, que é não garantir a coerência do corte:
O corte ilustrado (que pode ser entendido como um snapshot iniciado por P1) é incoerente (a soma de tokens é 2100).
É importante capturar também o estado dos canais de comunicação entre os processos!
Algoritmo de Chandy-Lamport
Este algoritmo estende o anterior de forma a capturar também o estado dos canais. Pressupõe que:
- não há falhas nos processos nem nos canais (ou seja, que são fiáveis)
- os canais são unidirecionais com uma implementação FIFO
- o grafo de processos e canais é fortemente ligado (isto é, existe um caminho entre quaisquer dois processos)
- qualquer processo pode iniciar uma snapshot global a qualquer momento
- os processos podem continuar a sua execução normal (e enviar/receber mensagens) enquanto a snapshot está a decorrer
A única diferença do algoritmo anterior é que o estado do canal também é guardado:
Estado dos canais
Cada processo guarda o seu estado local e, para cada canal de receção, guarda também o conjunto de mensagens recebidas após o snapshot. Desta forma, o processo regista quaisquer mensagens que tenham chegado depois de ter guardado o seu estado e antes do remetente ter registado o seu estado.
Pseudocódigo do algoritmo
Marker receiving rule for process p_i
On receipt of a marker message at p_i over channel c:
if (p_i has not yet recorded its state) it
records its process state now;
records the state of c as the empty set;
turns on recording of messages arriving over other incoming channels;
else
records the state of c as the set of messages it has received over c since it saved its state.
end if
Marker sending rule for process p_i
After p_i has recorded its state, for each outgoing channel c:
p_i sends one marker message over c
(before it sends any other message over c).Nota
Qualquer processo pode iniciar o algoritmo a qualquer momento. Este age como se tivesse recebido um marker (através de um canal inexistente) e segue a regra de receção de markers.
Neste algoritmo:
- nenhum processo decide quando termina
- todos os processos vão receber um marker e portanto guardar o seu estado
- todos os processos receberam um marker nos canais de receção e guardaram os seus estados
- existe a possibilidade de um servidor central obter todos os estados locais coerentes para construir um snapshot global
Exercício
Inicialmente, cada processo possui os tokens indicados na imagem. Sabendo que cada mensagem transfere 100 tokens entre 2 processos, qual vai ser o estado capturado pelo algoritmo Chandy-Lamport considerando que P1 inicia um snapshot no instante X?
R:
Justificação:
- P1: Enviou 2 mensagens, pelo que perdeu tokens
- P2: Não enviou nem recebeu mensagens, pelo que o número de tokens não se altera
- P3: Recebeu 2 mensagem de P1 e enviou 1 de volta, pelo que ganhou tokens
- C31: Desde que P1 enviou o primeiro marker até que recebeu de volta um de P3, recebeu nesse canal 1 mensagem, ou seja, tokens estavam a ser transferidos no canal
IMPORTANTE: A soma de tokens já se mantém a 2000! Ao escutar os canais, conseguimos saber que existe uma mensagem em trânsito de P3 para P1.
Nota
Mas será que um corte coerente garante que capturamos o estado global do sistema num determinado instante?
A verde está representado o estado real do sistema em cada fase e à direita temos o que foi capturado pelo snapshot : apesar de coerente, o sistema nunca esteve naquele estado...
Podemos verificar este acontecimento com o auxílio de vector clocks:
É possível observar que tanto é concorrente com como é com , pelo que o algoritmo não sabe em que ordem é que estes eventos aconteceram, já que os relógios de cada processo não estão sincronizados. O que o algoritmo consegue capturar é que o estado inicial é , após e é e por fim é .
Referências
- Coulouris et al - Distributed Systems: Concepts and Design (5th Edition)
- Secções 14.1, 14.2, 14.3, 14.4 e 14.5
- Coulouris et al - Distributed Systems: Concepts and Design (5th Edition) - Instructor's Manual
- Soluções dos exercícios 14.10, 14.11, 14.12 e 14.13
- van Steen and Tanenbaum - Distributed Systems
- Secções 5.1 e 5.2
- Departamento de Engenharia Informática - Slides de Sistemas Distribuídos (2022/2023)
- 3a Fundamentos: Tempo
- Paul Krzyzanowski - Assigning Lamport & Vector Timestamps
- Imagens dos exemplos de eventos e relógios lógicos
- Departamento de Engenharia Informática - Slides de Sistemas Distribuídos (2023/2024)
- SlidesTagus-Aula03b