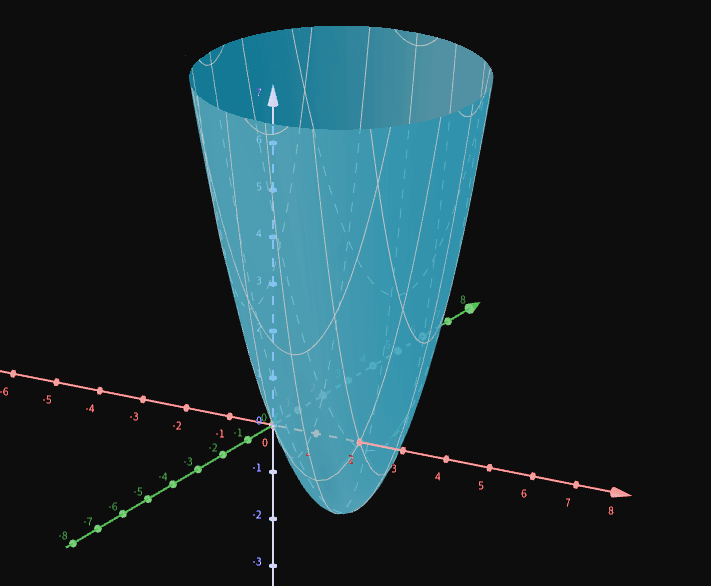
Basicamente é CDI 1 mas em dimensões superiores a 1.
Números: +, -, *, :
Sucessões: convergentes, divergentes, séries
Funções: continuidade, diferenciabilidade e integrabilidade
No entanto, em CDI 2:
Há noções e/ou resultados que migram para dim > 1.
Outros não
Surpresas - e.g. ponto de sela
Em CDI, o que conhecíamos que se f f f a a a ⇔ \Leftrightarrow ⇔ lim h → 0 f ( a + h ) − f ( a ) h \displaystyle \lim_{h\to 0}\frac{f(a+h)-f(a)}{h} h → 0 lim h f ( a + h ) − f ( a ) f ′ ( a ) f'(a) f ′ ( a )
No entanto, isto não está definido para d i m > 1 dim > 1 d im > 1 d i m > 1 dim > 1 d im > 1 1 ( 1 , 1 ) \frac{1}{(1,1)} ( 1 , 1 ) 1
Temos, então, de reformular a noção de derivada para a migrar para d i m > 1 dim > 1 d im > 1
f ′ ( a ) = lim h → 0 f ( a + h ) − f ( a ) h ⇔ 0 = lim h → 0 ( f ( a + h ) − f ( a ) h − h h f ′ ( a ) ) ⇔ 0 = lim h → 0 f ( a + h ) − f ( a ) − f ′ ( a ) h ⏞ o ( h ) h \begin{aligned}
f'( a) =\lim _{h\rightarrow 0}\frac{f( a+h) -f( a)}{h} & \Leftrightarrow 0=\lim _{h\rightarrow 0}\left(\frac{f( a+h) -f( a)}{h} -\frac{h}{h} f'( a)\right)\\
& \Leftrightarrow 0=\lim _{h\rightarrow 0}\frac{\overbrace{f( a+h) -f( a) -f'( a) h}^{o( h)}}{h}
\end{aligned} f ′ ( a ) = h → 0 lim h f ( a + h ) − f ( a ) ⇔ 0 = h → 0 lim ( h f ( a + h ) − f ( a ) − h h f ′ ( a ) ) ⇔ 0 = h → 0 lim h f ( a + h ) − f ( a ) − f ′ ( a ) h o ( h ) Chegamos assim a uma nova definição de derivada:
f e ˊ diferenci a ˊ vel em a ⇔ f ( a + h ) − f ( a ) − h f ′ ( a ) = o ( h ) , h → 0 f\ \text{é diferenciável em } a\Leftrightarrow f( a+h) -f( a) -hf'( a) =o( h) ,\ h\rightarrow 0 f e ˊ diferenci a ˊ vel em a ⇔ f ( a + h ) − f ( a ) − h f ′ ( a ) = o ( h ) , h → 0 ou seja,
f ( x ) = o ( x ) , x → a ⇔ lim x → a f ( x ) x = 0 f( x) =o( x) ,\ x\rightarrow a\Leftrightarrow \lim _{x\rightarrow a}\frac{f( x)}{x} =0 f ( x ) = o ( x ) , x → a ⇔ x → a lim x f ( x ) = 0 tip
o ( h ) o(h) o ( h ) h h h
Outra análise que podemos fazer, é pegar em
f ( a + h ) − f ( a ) − h f ′ ( a ) = o ( h ) ⇔ f ( a + h ) − f ( a ) = f ′ ( a ) h + o ( h ) , h → 0 f( a+h) -f( a) -hf'( a) =o( h) \Leftrightarrow f( a+h) -f( a) =f'( a) h+o( h) ,\ h\rightarrow 0 f ( a + h ) − f ( a ) − h f ′ ( a ) = o ( h ) ⇔ f ( a + h ) − f ( a ) = f ′ ( a ) h + o ( h ) , h → 0 e chegar à conclusão que a variação da função, quando passa de a a a a + h a+h a + h o ( h ) o(h) o ( h ) f f f a a a h h h f ′ ( a ) h f'(a)h f ′ ( a ) h h h h
Com esta reformulação, a derivada já migra para d i m > 1 dim > 1 d im > 1 existência desta transformação linear .
De facto, sempre foi, mas em d i m = 1 dim = 1 d im = 1
Distância de x x x y y y d ( x , y ) d(x,y) d ( x , y ) d ( x , y ) = ∣ x − y ∣ d(x,y)= |x-y| d ( x , y ) = ∣ x − y ∣
O que vai ser a distância em d i m > 1 dim > 1 d im > 1
Para duas dimensões:
p ( x 1 , y 1 ) , q ( x 2 , y 2 ) , d ( p , q ) = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 p(x_1,y_1),\quad q(x_2,y_2),\quad d(p,q) = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} p ( x 1 , y 1 ) , q ( x 2 , y 2 ) , d ( p , q ) = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 Para três dimensões:
p ( x 1 , y 1 , z 1 ) , q ( x 2 , y 2 , z 2 ) , d ( p , q ) = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 p(x_1,y_1, z_1),\quad q(x_2,y_2,z_2),\quad d(p,q) = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2} p ( x 1 , y 1 , z 1 ) , q ( x 2 , y 2 , z 2 ) , d ( p , q ) = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 Para N N N
d ( x , y ) = ∑ i = 1 N ( x i − y i ) 2 d(x,y)=\sqrt{\sum_{i=1}^{N}(x_i-y_i)^2} d ( x , y ) = i = 1 ∑ N ( x i − y i ) 2
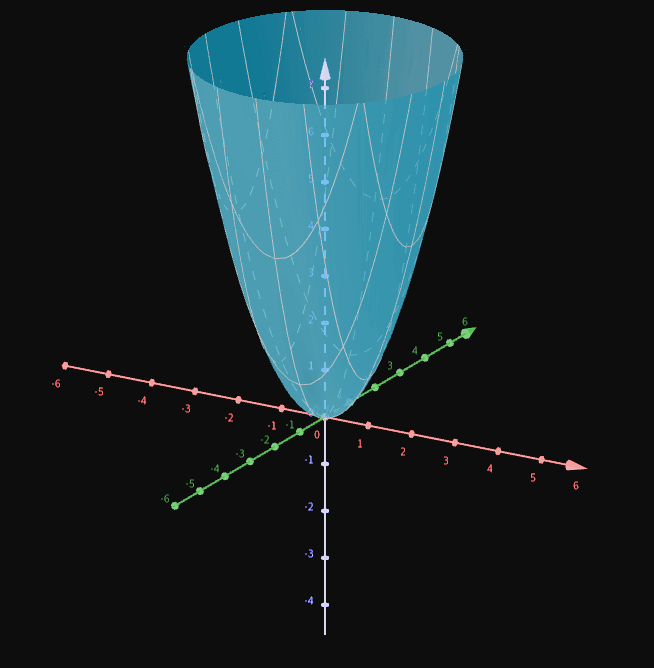
f ( x , y ) = x 2 + y 2 = ( ( x − 0 ) 2 + ( y − 0 ) 2 ) 2 = ( d ( ( x , y ) , ( 0 , 0 ) ) ) 2 \displaystyle f(x,y)=x^2+y^2=\left(\sqrt{(x-0)^2+(y-0)^2}\right)^2=\left(d((x,y), (0,0))\right)^2 f ( x , y ) = x 2 + y 2 = ( ( x − 0 ) 2 + ( y − 0 ) 2 ) 2 = ( d (( x , y ) , ( 0 , 0 )) ) 2
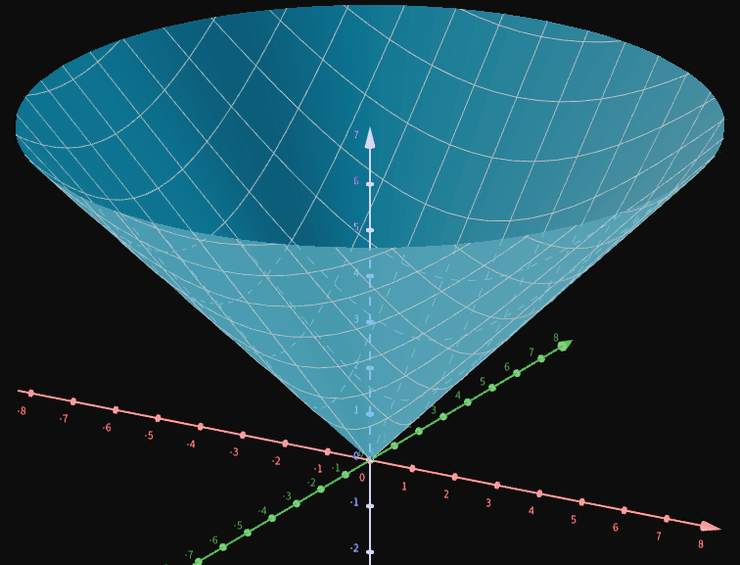
g ( x , y ) = x 2 + y 2 = ( x + 0 ) 2 + ( y + 0 ) 2 = d ( ( x , y ) , ( 0 , 0 ) ) \displaystyle g( x,y) =\sqrt{x^{2} +y^{2}} =\sqrt{( x+0)^{2} +( y+0)^{2}} =d(( x,y) ,( 0,0)) g ( x , y ) = x 2 + y 2 = ( x + 0 ) 2 + ( y + 0 ) 2 = d (( x , y ) , ( 0 , 0 ))
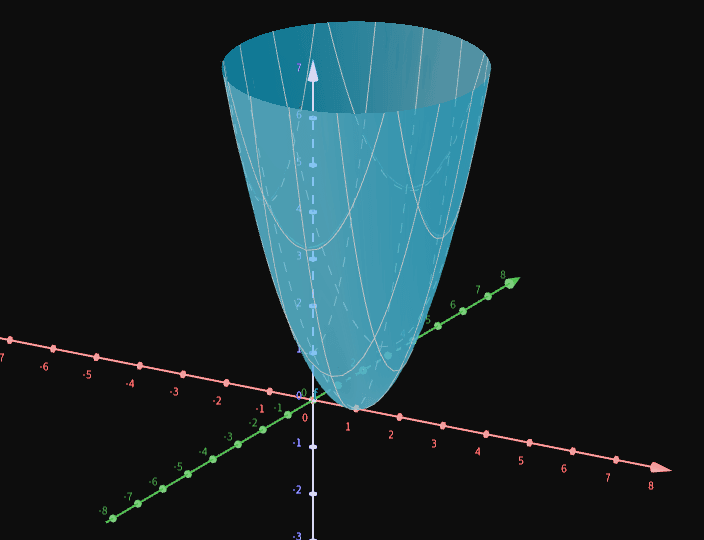
h ( x , y ) = x 2 − 2 x + 1 + y 2 = ( x − 1 ) 2 + ( y + 0 ) 2 = ( ( x − 1 ) 2 + ( y + 0 ) 2 ) 2 = ( d ( ( x , y ) , ( 1 , 0 ) ) ) 2 \displaystyle h( x,y) =x^{2} -2x+1+y^{2} =( x-1)^{2} +( y+0)^{2} =\left(\sqrt{( x-1)^{2} +( y+0)^{2}}\right)^{2} =( d(( x,y) ,( 1,0)))^{2} h ( x , y ) = x 2 − 2 x + 1 + y 2 = ( x − 1 ) 2 + ( y + 0 ) 2 = ( ( x − 1 ) 2 + ( y + 0 ) 2 ) 2 = ( d (( x , y ) , ( 1 , 0 )) ) 2
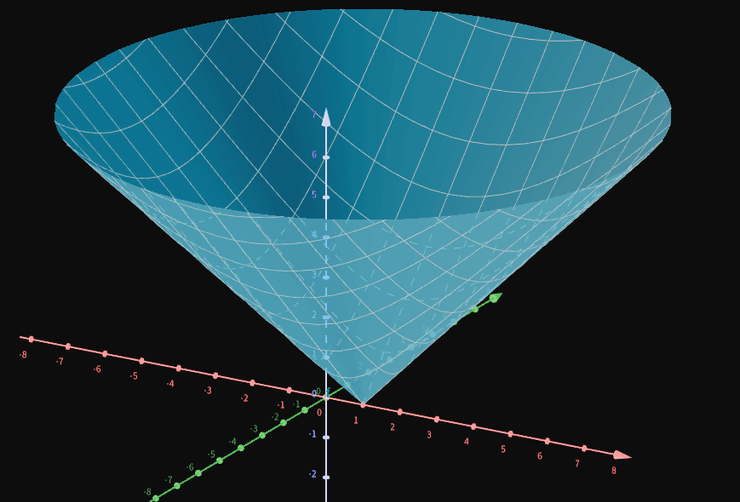
h ‾ ( x , y ) = x 2 − 2 x + 1 + y 2 = ( x − 1 ) 2 + ( y + 0 ) 2 = ( x − 1 ) 2 + ( y + 0 ) 2 = d ( ( x , y ) , ( 1 , 0 ) ) \displaystyle \overline{h}( x,y) =\sqrt{x^{2} -2x+1+y^{2}} =\sqrt{( x-1)^{2} +( y+0)^{2}} =\sqrt{( x-1)^{2} +( y+0)^{2}} =d(( x,y) ,( 1,0)) h ( x , y ) = x 2 − 2 x + 1 + y 2 = ( x − 1 ) 2 + ( y + 0 ) 2 = ( x − 1 ) 2 + ( y + 0 ) 2 = d (( x , y ) , ( 1 , 0 ))
i ( x , y ) = x 2 − 2 x + y 2 − 2 y = x 2 − 2 x + 1 + y 2 − 2 y + 1 − 2 = ( x − 1 ) 2 + ( y − 1 ) 2 − 2 = = ( ( x − 1 ) 2 + ( y − 1 ) 2 ) 2 − 2 = ( d ( ( x , y ) , ( 1 , 1 ) ) ) 2 − 2 \begin{aligned}
i( x,y) & =x^{2} -2x+y^{2} -2y=x^{2} -2x+1+y^{2} -2y+1-2=( x-1)^{2} +( y-1)^{2} -2=\\
& =\left(\sqrt{( x-1)^{2} +( y-1)^{2}}\right)^{2} -2=( d(( x,y) ,( 1,1)))^{2} -2
\end{aligned} i ( x , y ) = x 2 − 2 x + y 2 − 2 y = x 2 − 2 x + 1 + y 2 − 2 y + 1 − 2 = ( x − 1 ) 2 + ( y − 1 ) 2 − 2 = = ( ( x − 1 ) 2 + ( y − 1 ) 2 ) 2 − 2 = ( d (( x , y ) , ( 1 , 1 )) ) 2 − 2
Slides: