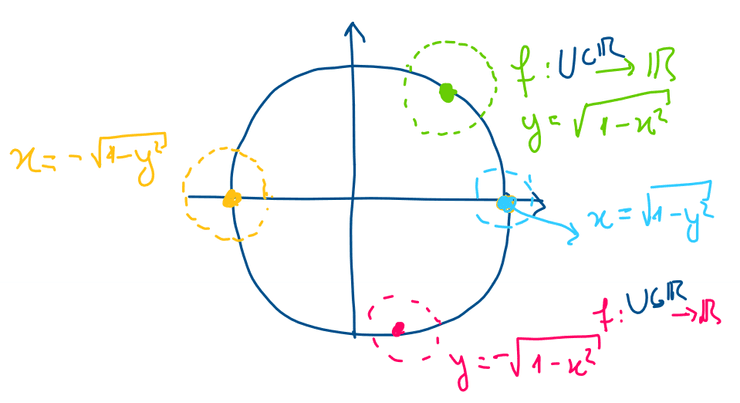Um conjunto é uma variedade de dim m \dim m dim m C 1 C^1 C 1 m m m
DEFINIÇÃO
M ⊂ R n M \subset \R^n M ⊂ R n m m m ∀ a ∈ M \forall a \in M ∀ a ∈ M M M M f : U ⊂ R m → R n − m f: U\subset \R^m \to \R^{n - m} f : U ⊂ R m → R n − m C 1 C^1 C 1
Tomando como exemplo os seguintes conjuntos:
M = { ( x , y ) ∈ R 2 : x 2 + y 2 = 1 } M= \{(x,y) \in \R^2: x^2+y^2=1\} M = {( x , y ) ∈ R 2 : x 2 + y 2 = 1 }
É variedade de dimensão 1.
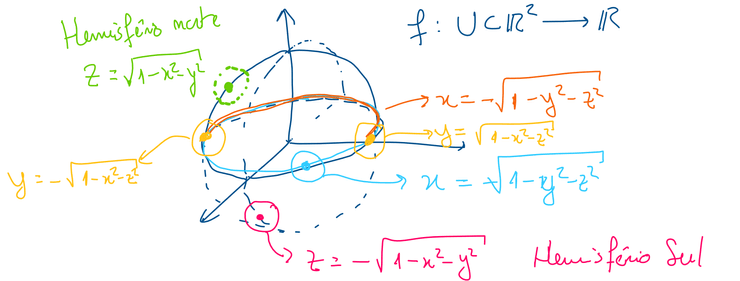
M = { ( x , y , z ) ∈ R 3 : x 2 + y 2 + z 2 = 1 } M = \{(x,y,z) \in \R^3: x^2+y^2+z^2 = 1\} M = {( x , y , z ) ∈ R 3 : x 2 + y 2 + z 2 = 1 }
É variedade de dimensão 2.
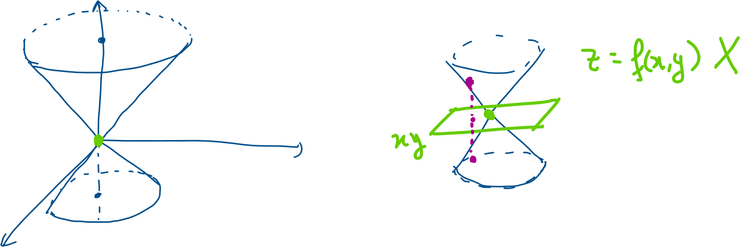
M = { ( x , y , z ) ∈ R 3 : x 2 + y 2 = z 2 } M= \{(x,y,z) \in \R^3: x^2 + y^2 = z^2\} M = {( x , y , z ) ∈ R 3 : x 2 + y 2 = z 2 }
Não é variedade.
Na origem não é possível escrever nenhuma variável em função das outras duas, pois tem um "bico".
M = { ( x , y , z ) ∈ R 3 : z = x + y } M = \{(x,y,z) \in \R^3: z=x+y\} M = {( x , y , z ) ∈ R 3 : z = x + y } z = f ( x , y ) = x + y z=f(x,y) = x+y z = f ( x , y ) = x + y variedade de dimensão 2 .
Se considerarmos um conjunto de nível:
M = { x ∈ R n : F ( x ) = 0 } F : R n → R n − m C 1 \begin{array}{lll}
M = \{x \in \R^n: F(x) = 0\} & F: \R^n \to \R^{n-m} & C^1
\end{array} M = { x ∈ R n : F ( x ) = 0 } F : R n → R n − m C 1 Então, M M M dim m \dim\ m dim m ∀ a ∈ M \forall a \in M ∀ a ∈ M Teorema da Função Implícita com m m m
Basta encontrar m m m det D F ≠ 0 ⟹ caracter ı ˊ stica m a ˊ xima n − m \det DF \ne 0 \implies \text{característica máxima}~n - m det D F = 0 ⟹ caracter ı ˊ stica m a ˊ xima n − m
TEOREMA
O conjunto de nível é uma variedade de dim m \dim\ m dim m D F DF D F característica máxima.
Exemplos Considerando
M = { x 2 + y 2 = 1 } = { F ( x , y ) = x 2 + y 2 − 1 = 0 } , F ∈ C 1 M=\{x^2+y^2 = 1\} = \{F(x,y) = x^2+y^2-1=0\}, F \in C^1 M = { x 2 + y 2 = 1 } = { F ( x , y ) = x 2 + y 2 − 1 = 0 } , F ∈ C 1 D F = [ 2 x 2 y ] DF = \begin{bmatrix}
2x & 2y
\end{bmatrix} D F = [ 2 x 2 y ] Quando car D F ≠ 1 \car DF \ne 1 car D F = 1 x , y = 0 x,y = 0 x , y = 0
Logo, car D F \car DF car D F M M M 1 1 1
Considerando
M = { x 2 + y 2 + z 2 = N } = F ( x , y , z ) = x 2 + y 2 + z 2 − N = 0 , F ∈ C 1 M = \{ x^2+y^2 + z^2 = N \} = {F(x,y,z) = x^2+y^2+z^2-N = 0}, F \in C^1 M = { x 2 + y 2 + z 2 = N } = F ( x , y , z ) = x 2 + y 2 + z 2 − N = 0 , F ∈ C 1 D F = [ 2 x 2 y 2 z ] DF = \begin{bmatrix}
2x & 2y & 2z
\end{bmatrix} D F = [ 2 x 2 y 2 z ] Quando car D F \car DF car D F x , y , z = 0 x,y,z=0 x , y , z = 0
Logo, D F DF D F M M M dim 3 − 1 = 2 \dim 3-1 = 2 dim 3 − 1 = 2
Considerando
M = { x 2 + y 2 − z 2 = 0 } M = \{x^2+y^2-z^2 = 0\} M = { x 2 + y 2 − z 2 = 0 } isto é, um cone.
D F = [ 2 x 2 y − 2 z ] DF = \begin{bmatrix}
2x & 2y & -2z
\end{bmatrix} D F = [ 2 x 2 y − 2 z ] Então, quando car = 0 \car = 0 car = 0 x , y , z = 0 x,y,z=0 x , y , z = 0
Como este ponto pertence ao conjunto, M M M
Considerando
A = { ( x , y , z ) ∈ R 3 : x 2 + y 2 + z 2 = 1 , x + y − z = 0 } A = \{(x,y,z) \in \R^3: x^2+y^2+z^2 = 1, x+y-z=0 \} A = {( x , y , z ) ∈ R 3 : x 2 + y 2 + z 2 = 1 , x + y − z = 0 } Então, podemos escrever a função:
F ( x , y , z ) = ( x 2 + y 2 + z 2 − 1 , x + y − z ) F : R 3 → R 2 \begin{array}{ll}
F(x,y,z) = (x^2+y^2+z^2-1, x+y-z)
& F: \R^3 \to \R^2
\end{array} F ( x , y , z ) = ( x 2 + y 2 + z 2 − 1 , x + y − z ) F : R 3 → R 2 A matriz D F DF D F
D F ( x , y , z ) = [ 2 x 2 y 2 z 1 1 − 1 ] DF(x,y,z) = \begin{bmatrix}
2x & 2y & 2z\\
1 & 1 & -1
\end{bmatrix} D F ( x , y , z ) = [ 2 x 1 2 y 1 2 z − 1 ] Pelo que:
car = 0 \car = 0 car = 0 car = 1 \car = 1 car = 1 ( 2 x , 2 y , 2 z ) = λ ( 1 , 1 , − 1 ) (2x, 2y, 2z) = \lambda (1, 1, -1) ( 2 x , 2 y , 2 z ) = λ ( 1 , 1 , − 1 ) x = λ 2 y = λ 2 z = − λ 2 \begin{array}{lll}
x=\frac{\lambda}{2} &
y=\frac{\lambda}{2} &
z=-\frac{\lambda}{2}
\end{array} x = 2 λ y = 2 λ z = − 2 λ Substituindo no conjunto:
{ ( λ 2 ) 2 + ( λ 2 ) 2 + ( λ 2 ) 2 = 1 λ 2 + λ 2 + λ 2 = 0 ⇔ { λ = 0 0 = 1 ⇔ imposs ı ˊ vel \begin{cases}
\left(\frac{\lambda}{2} \right)^2 + \left(\frac{\lambda}{2} \right)^2 + \left(\frac{\lambda}{2} \right)^2 = 1\\
\frac{\lambda}{2} + \frac{\lambda}{2} + \frac{\lambda}{2} = 0
\end{cases}
\Leftrightarrow
\begin{cases}
\lambda = 0\\
0 = 1
\end{cases}
\Leftrightarrow
\text{impossível} { ( 2 λ ) 2 + ( 2 λ ) 2 + ( 2 λ ) 2 = 1 2 λ + 2 λ + 2 λ = 0 ⇔ { λ = 0 0 = 1 ⇔ imposs ı ˊ vel Então, o ponto ( λ 2 , λ 2 , λ 2 ) (\frac{\lambda}{2},\frac{\lambda}{2},\frac{\lambda}{2}) ( 2 λ , 2 λ , 2 λ ) A A A
Logo, ∀ x , y , z ∈ A \forall x,y,z \in A ∀ x , y , z ∈ A car D F ( x , y , z ) = 2 \car DF(x,y,z) = 2 car D F ( x , y , z ) = 2
A A A dim 3 − 2 = 1 \dim 3 -2 = 1 dim 3 − 2 = 1
A A A R 3 \R^3 R 3
DEFINIÇÃO
Seja M M M dim m ⊂ R n \dim m \subset R^n dim m ⊂ R n g : V → M g: V \to M g : V → M
V ∈ R m V \in \R^m V ∈ R m g ∈ C 1 g \in C^1 g ∈ C 1 g g g D g Dg D g Pode não ser possível parametrizar de uma só vez toda a variedade.
Como exemplo, temos o seguinte conjunto (circunferência de raio 1):
A sua parametrização é g ( t ) = ( cos t , sin t ) , t ∈ ] 0 , 2 π [ g(t) = (\cos t, \sin t), t \in ]0, 2\pi[ g ( t ) = ( cos t , sin t ) , t ∈ ] 0 , 2 π [
Exemplos Seja f ∈ C 1 f \in C^1 f ∈ C 1 ] a , b [ ]a,b[ ] a , b [
M = { ( x , y ) ∈ R 2 : y = f ( x ) } ⊂ R 2 M = \{(x,y) \in \R^2: y = f(x)\} \subset \R^2 M = {( x , y ) ∈ R 2 : y = f ( x )} ⊂ R 2 Podemos então descrever este conjunto pela função g g g
g ( t ) = ( t , f ( t ) ) , t ∈ ] a , b [ g(t) = (t, f(t)), t \in ]a,b[ g ( t ) = ( t , f ( t )) , t ∈ ] a , b [ Será que g g g
g g g C 1 C^1 C 1 t ∈ t t \in t t ∈ t C 1 C^1 C 1 f ∈ C 1 f \in C^1 f ∈ C 1
será que g g g
g ( t 1 ) = g ( t 2 ) ⇔ ( t 1 , f ( t 1 ) ) = ( t 2 , f ( t 2 ) ) ⇒ t 1 = t 2 g(t_1) = g(t_2) \Leftrightarrow (t_1, f(t_1)) = (t_2, f(t_2)) \Rightarrow t_1 = t_2 g ( t 1 ) = g ( t 2 ) ⇔ ( t 1 , f ( t 1 )) = ( t 2 , f ( t 2 )) ⇒ t 1 = t 2
D g ( t ) = [ 1 f ′ ( t ) ] Dg(t) = \begin{bmatrix}1\\f'(t)\end{bmatrix} D g ( t ) = [ 1 f ′ ( t ) ] D g Dg D g
Logo, g g g M M M
Considerando
P = { ( x , y , z ) ∈ R 3 , z = x 2 + y 2 , z < 1 } P = \{(x,y,z) \in \R^3, z=x^2+y^2, z <1\} P = {( x , y , z ) ∈ R 3 , z = x 2 + y 2 , z < 1 }
Sabemos que P P P f ( x , y ) = x 2 + y 2 f(x,y) = x^2+y^2 f ( x , y ) = x 2 + y 2 x 2 + y 2 < 1 x^2+y^2 < 1 x 2 + y 2 < 1
Então podemos escrever a função g g g P P P
g ( x , y ) = ( x , y , f ( x , y ) ) , x 2 + y 2 < 1 g(x,y) = (x,y,f(x,y)), \quad x^2+y^2 < 1 g ( x , y ) = ( x , y , f ( x , y )) , x 2 + y 2 < 1
Outra parametrização possível, é usar as coordenadas cilíndricas:
{ x = r cos θ y = r sin θ z = z \begin{cases}
x = r \cos \theta\\
y = r \sin \theta\\
z = z
\end{cases} ⎩ ⎨ ⎧ x = r cos θ y = r sin θ z = z Então obtemos:
g ( r , θ ) = ( r cos θ , r sin θ , r 2 ) , r ∈ ] 0 , 1 ] , θ ∈ ] 0 , 2 π [ g(r,\theta) = (r \cos \theta, r \sin \theta, r^2), \quad r \in ]0, 1], \theta \in ]0, 2\pi[ g ( r , θ ) = ( r cos θ , r sin θ , r 2 ) , r ∈ ] 0 , 1 ] , θ ∈ ] 0 , 2 π [
Considerando
M = { ( x , y ) ∈ R 2 : x > 0 , x 2 + y 2 = 1 } M = \{(x,y) \in \R^2 : x>0, x^2+y^2=1 \} M = {( x , y ) ∈ R 2 : x > 0 , x 2 + y 2 = 1 } variedade de dim 1 \dim 1 dim 1 semi-circulo .
Como x > 0 ⟹ x = 1 − y 2 x >0 \implies x=\sqrt{1-y^2} x > 0 ⟹ x = 1 − y 2
g ( y ) = ( 1 − y 2 , y ) g : ] − 1 , 1 [ → M \begin{array}{ll}
g(y) = (\sqrt{1-y^2}, y) & g : ]-1, 1[ \to M
\end{array} g ( y ) = ( 1 − y 2 , y ) g : ] − 1 , 1 [ → M Verificando agora as condições da parametrização:
g ∈ C 1 g \in C^1 g ∈ C 1 g g g g ( y 1 ) = g ( y 2 ) ⟹ ( y 1 2 , y 1 ) = ( 1 − y 2 2 , y 2 ) ⟹ y 1 = y 2 g(y_1) = g(y_2) \implies (\sqrt{y^2_1}, y_1) = (\sqrt{1-y^2_2}, y_2) \implies y_1=y_2 g ( y 1 ) = g ( y 2 ) ⟹ ( y 1 2 , y 1 ) = ( 1 − y 2 2 , y 2 ) ⟹ y 1 = y 2 D g ( y ) = [ − y 1 − y 2 1 ] Dg(y)= \begin{bmatrix} -\frac{y}{\sqrt{1-y^2}} \\ 1\end{bmatrix} D g ( y ) = [ − 1 − y 2 y 1 ] Alternativamente, podemos usar coordenadas polares:
g ( θ ) = ( cos θ , sin θ ) θ ∈ ] − π 2 , π 2 [ \begin{array}{ll}
g(\theta) = (\cos \theta, \sin \theta) &
\theta \in \left]-\frac{\pi}{2}, \frac{\pi}{2}\right[
\end{array} g ( θ ) = ( cos θ , sin θ ) θ ∈ ] − 2 π , 2 π [ Verificando novamente as condições da parametrização:
g ∈ C 1 g \in C^1 g ∈ C 1 g g g D g ( θ ) = [ − sin θ cos θ ] Dg(\theta) = \begin{bmatrix} - \sin \theta \\ \cos \theta \end{bmatrix} D g ( θ ) = [ − sin θ cos θ ] D g Dg D g sin θ , cos θ = 0 \sin \theta, \cos \theta = 0 sin θ , cos θ = 0 M M M sin 2 θ + cos 2 θ = 1 \sin^2\theta + \cos^2\theta = 1 sin 2 θ + cos 2 θ = 1 Logo, g g g M M M
Considerando
M = { ( x , y , z ) : x 2 + y 2 + z 2 = 1 , z > 0 } M = \{(x,y,z): x^2+y^2+z^2 = 1, z > 0\} M = {( x , y , z ) : x 2 + y 2 + z 2 = 1 , z > 0 }
Utilizando as coordenadas esféricas, com r = 1 r=1 r = 1
g ( θ , φ ) = ( cos θ sin φ , sin θ sin φ , cos φ ) θ ∈ ] 0 , 2 π [ , φ ∈ ] 0 , π 2 [ \begin{array}{ll}
g(\theta, \varphi) = (\cos \theta \sin \varphi, \sin \theta \sin \varphi, \cos \varphi) &
\theta \in \left]0, 2\pi\right[, \varphi \in \left]0, \frac{\pi}{2}\right[
\end{array} g ( θ , φ ) = ( cos θ sin φ , sin θ sin φ , cos φ ) θ ∈ ] 0 , 2 π [ , φ ∈ ] 0 , 2 π [
g ∈ C 1 g \in C^1 g ∈ C 1
g g g
D g Dg D g
D g ( θ , φ ) = [ − sin θ sin φ cos θ cos φ cos θ sin φ sin θ cos φ 0 − sin φ ] Dg(\theta, \varphi) = \begin{bmatrix}
\smartcolor{blue}{-\sin \theta \sin \varphi} & \cos \theta \cos \varphi\\
\smartcolor{blue}{\cos \theta \sin \varphi} & \sin \theta \cos \varphi\\
0 & \smartcolor{orange}{-\sin \varphi}
\end{bmatrix} D g ( θ , φ ) = − sin θ sin φ cos θ sin φ 0 cos θ cos φ sin θ cos φ − sin φ Em φ ∈ ] 0 , π 2 [ \varphi \in \left]0, \frac{\pi}{2}\right[ φ ∈ ] 0 , 2 π [ − sin φ < 0 \smartcolor{orange}{-\sin \varphi} < 0 − sin φ < 0
Também temos que
{ − sin θ sin φ = 0 cos θ sin φ = 0 ⇒ sin θ , cos θ = 0 \begin{cases}
\smartcolor{blue}{-\sin \theta \sin \varphi} = 0\\
\smartcolor{blue}{\cos \theta \sin \varphi} = 0
\end{cases}
\Rightarrow
\sin\theta, \cos\theta = 0 { − sin θ sin φ = 0 cos θ sin φ = 0 ⇒ sin θ , cos θ = 0 que é impossível em M M M sin 2 θ + cos 2 θ = 1 \sin^2 \theta + \cos^2 \theta = 1 sin 2 θ + cos 2 θ = 1
Logo, g g g M M M
Considerando
M = { ( x , y , z ) ∈ R 3 : x 2 + y 2 + z 2 = 1 , x = y } M = \{(x,y,z) \in \R^3: x^2+y^2+z^2 = 1, x = y \} M = {( x , y , z ) ∈ R 3 : x 2 + y 2 + z 2 = 1 , x = y }
que se sabe ser uma variedade de dim 1 \dim 1 dim 1
Podemos substituir y y y x x x 2 x 2 + z 2 = 1 ⇔ ( 2 x ) 2 + z 2 = 1 2x^2+z^2=1 \Leftrightarrow (\sqrt{2} x)^2+z^2 = 1 2 x 2 + z 2 = 1 ⇔ ( 2 x ) 2 + z 2 = 1
Podemos agora aplicar coordenadas cilíndricas modificadas:
{ 2 x = cos θ z = sin θ ⇔ { x = 1 2 cos θ z = sin θ \begin{cases}
\sqrt{2} x = \cos \theta\\
z = \sin \theta
\end{cases}
\Leftrightarrow
\begin{cases}
x = \frac{1}{\sqrt{2}} \cos \theta\\
z = \sin \theta
\end{cases} { 2 x = cos θ z = sin θ ⇔ { x = 2 1 cos θ z = sin θ Como x = y x = y x = y y = 1 2 cos θ y = \frac{1}{\sqrt{2}} \cos \theta y = 2 1 cos θ
Obtemos assim a parametrização:
g ( θ ) = ( 1 2 cos θ , 1 2 cos θ , sin θ ) θ ∈ ] 0 , 2 π [ \begin{array}{ll}
g(\theta) = \left(\frac{1}{\sqrt{2}} \cos \theta, \frac{1}{\sqrt{2}} \cos \theta, \sin \theta\right) & \theta \in ]0, 2\pi[
\end{array} g ( θ ) = ( 2 1 cos θ , 2 1 cos θ , sin θ ) θ ∈ ] 0 , 2 π [ DEFINIÇÃO
M M M dim m ⊂ R n \dim m \subset \R^n dim m ⊂ R n v ∈ R n v \in \R^n v ∈ R n a ∈ M a \in M a ∈ M
v v v M M M a a a γ \gamma γ M M M γ ( 0 ) = a \gamma (0) = a γ ( 0 ) = a γ ′ ( 0 ) = v \gamma'(0) = v γ ′ ( 0 ) = v
Espaço Tangente a M M M a a a
T a M = { vetores tangentes a M no ponto a } T_aM = \{\text{vetores tangentes a } M \text{ no ponto } a\} T a M = { vetores tangentes a M no ponto a } é espaço vetorial de dimensão m m m
Espaço Normal a M M M a a a
( T a M ) ⊥ = { vetores perpendiculares a T a M } (T_aM)^\perp = \{\text{vetores perpendiculares a } T_aM\} ( T a M ) ⊥ = { vetores perpendiculares a T a M } é espaço vetorial de dimensão n − m n-m n − m
Pode-se facilmente obter o espaço normal através da matriz jacobiana D F DF D F γ \gamma γ a a a
Vejamos um exemplo:
Considerando o conjunto S = { ( x , y , z ) ∈ R 3 : z = x 4 + y 3 } S = \{(x,y,z) \in \R^3: z = x^4+y^3\} S = {( x , y , z ) ∈ R 3 : z = x 4 + y 3 } a = ( 1 , 1 , 2 ) a = (1,1,2) a = ( 1 , 1 , 2 ) S S S dim 2 \dim 2 dim 2
Podemos escrever o seguinte:
S = { ( x , y , z ) ∈ R 3 : F = x 4 + y 3 − z = 0 } F ∈ C 1 \begin{array}{ll}
S = \{(x,y,z) \in \R^3: F = x^4 +y^3 - z = 0\} & F \in C^1
\end{array} S = {( x , y , z ) ∈ R 3 : F = x 4 + y 3 − z = 0 } F ∈ C 1 D F ( x , y , z ) = [ 4 x 3 3 y 2 − 1 ] DF(x,y,z) = \begin{bmatrix}
4x^3 & 3y^2 & -1
\end{bmatrix} D F ( x , y , z ) = [ 4 x 3 3 y 2 − 1 ] D F ( 1 , 1 , 2 ) = [ 4 3 − 1 ] DF(1,1,2) = \begin{bmatrix}
4 & 3 & -1
\end{bmatrix} D F ( 1 , 1 , 2 ) = [ 4 3 − 1 ] ( T ( 1 , 1 , 2 ) S ) ⊥ = L { ( 4 , 3 , − 1 ) } que e ˊ uma reta (T_{(1,1,2)}S)^{\perp} = \mathcal{L} \{(4,3,-1)\}\ \text{que é uma reta} ( T ( 1 , 1 , 2 ) S ) ⊥ = L {( 4 , 3 , − 1 )} que e ˊ uma reta ( x , y , z ) ∈ T ( 1 , 1 , 2 ) S : ( x , y , z ) ⋅ ( 4 , 3 , − 1 ) = 0 ⇔ 4 x + 3 y − z = 0 (um plano) (x,y,z) \in T_{(1,1,2)}S: (x,y,z) \cdot (4,3,-1) = 0 \Leftrightarrow 4x+3y-z=0\ \text{(um plano)} ( x , y , z ) ∈ T ( 1 , 1 , 2 ) S : ( x , y , z ) ⋅ ( 4 , 3 , − 1 ) = 0 ⇔ 4 x + 3 y − z = 0 (um plano) Escolhendo assim dois pontos distintos pertencentes ao plano:
T ( 1 , 1 , 2 ) S = L { ( 1 , − 1 , 1 ) , ( 0 , 1 , 3 ) } T_{(1,1,2)} S = \mathcal{L} \{(1,-1,1), (0,1,3)\} T ( 1 , 1 , 2 ) S = L {( 1 , − 1 , 1 ) , ( 0 , 1 , 3 )} Mais Exemplos Considerando agora o conjunto L L L
L = { ( x , y , z ) ∈ R 3 : z = x 4 + y , x + y + z = 6 } L = \{(x,y,z) \in \R^3: z=x^4+y, x+y+z=6\} L = {( x , y , z ) ∈ R 3 : z = x 4 + y , x + y + z = 6 } Será que é variedade? Se sim, qual a sua dimensão?
Qual o espaço tangente e normal no ponto ( 1 , 2 , 3 ) (1,2,3) ( 1 , 2 , 3 )
Comecemos por escrever o conjunto na forma de conjunto de nível:
F ( x , y , z ) = ( x 4 + y − z , x + y + z − 6 ) L = { ( x , y , z ) ∈ R 3 : F = ( 0 , 0 ) } \begin{array}{c}
F(x,y,z) = (x^4+y-z, x+y+z-6)\\
L=\{(x,y,z) \in \R^3: F=(0,0)\}
\end{array} F ( x , y , z ) = ( x 4 + y − z , x + y + z − 6 ) L = {( x , y , z ) ∈ R 3 : F = ( 0 , 0 )} Calculando agora a jacobiana de F F F
D F ( x , y , z ) = [ 4 x 3 1 − 1 1 1 1 ] DF(x,y,z) = \begin{bmatrix}
4x^3 & 1 & -1\\
1 & 1 & 1
\end{bmatrix} D F ( x , y , z ) = [ 4 x 3 1 1 1 − 1 1 ] D F DF D F
Logo L L L dim 3 − 2 = 1 \dim 3 - 2 = 1 dim 3 − 2 = 1
Tomando agora a jacobiana no ponto a = ( 1 , 2 , 3 ) a = (1,2,3) a = ( 1 , 2 , 3 )
D F ( 1 , 2 , 3 ) = [ 4 1 − 1 1 1 1 ] DF (1,2,3) = \begin{bmatrix}
4 & 1 & -1\\
1 & 1 & 1
\end{bmatrix} D F ( 1 , 2 , 3 ) = [ 4 1 1 1 − 1 1 ] Ficamos assim a saber o seu espaço normal:
( T ( 1 , 2 , 3 ) L ) ⊥ = L { ( 4 , 1 , − 1 ) , ( 1 , 1 , 1 ) } (T_{(1,2,3)}L)^{\perp} = \mathcal{L} \{(4,1,-1), (1,1,1)\} ( T ( 1 , 2 , 3 ) L ) ⊥ = L {( 4 , 1 , − 1 ) , ( 1 , 1 , 1 )} Qual o valor de T ( 1 , 2 , 3 ) L T_{(1,2,3)}L T ( 1 , 2 , 3 ) L
( x , y , z ) ∈ T ( 1 , 2 , 3 ) L ⇔ { ( x , y , z ) ⋅ ( 4 , 1 , − 1 ) = 0 ( x , y , z ) ⋅ ( 1 , 1 , 1 ) = 0 ⇔ { 4 x + y − z = 0 x + y + z = 0 ⇔ { 5 x + 2 y = 0 3 x − 2 z = 0 \begin{aligned}
(x,y,z) \in T_{(1,2,3)}L &\Leftrightarrow \begin{cases}
(x,y,z) \cdot (4,1,-1) = 0\\
(x,y,z) \cdot (1,1,1) = 0
\end{cases}\\
& \Leftrightarrow \begin{cases}
4x+y-z=0\\
x+y+z=0
\end{cases}\\
& \Leftrightarrow \begin{cases}
5x+2y=0\\
3x-2z = 0
\end{cases}
\end{aligned} ( x , y , z ) ∈ T ( 1 , 2 , 3 ) L ⇔ { ( x , y , z ) ⋅ ( 4 , 1 , − 1 ) = 0 ( x , y , z ) ⋅ ( 1 , 1 , 1 ) = 0 ⇔ { 4 x + y − z = 0 x + y + z = 0 ⇔ { 5 x + 2 y = 0 3 x − 2 z = 0 Podemos escolher qualquer ponto que satisfaça o sistema acima, por exemplo: ( 1 , − 5 2 , 3 2 ) (1, -\frac{5}{2}, \frac{3}{2}) ( 1 , − 2 5 , 2 3 )
T ( 1 , 2 , 3 ) L = L { ( 1 , − 5 2 , 3 2 ) } T_{(1,2,3)}L = \mathcal{L}\left\{\left(1,-\frac{5}{2}, \frac{3}{2}\right)\right\} T ( 1 , 2 , 3 ) L = L { ( 1 , − 2 5 , 2 3 ) } Suponhamos que g g g g : V → M g: V \to M g : V → M M = { F = 0 } M = \{F = 0\} M = { F = 0 } g ( t 0 ) = a g(t_0) = a g ( t 0 ) = a
As colunas de D g ( t 0 ) Dg(t_0) D g ( t 0 )
T a M = L { colunas de D g ( t 0 ) } T_aM = \mathcal{L} \{\text{colunas de}\ Dg(t_0)\} T a M = L { colunas de D g ( t 0 )} Demonstração 0 = F ( g ( t ) ) ⟹ 0 = D ( F ( g ( t ) ) ) = D F ( g ( t ) ) ⋅ D g ( t ) 0=F(g(t)) \implies 0 = D(F(g(t))) = DF(g(t))\cdot Dg(t) 0 = F ( g ( t )) ⟹ 0 = D ( F ( g ( t ))) = D F ( g ( t )) ⋅ D g ( t ) Quando t = t 0 t=t_0 t = t 0 D F ( a ) ⋅ D g ( t 0 ) = 0 DF(a) \cdot Dg(t_0)=0 D F ( a ) ⋅ D g ( t 0 ) = 0 D F ( a ) DF(a) D F ( a ) D g ( t 0 ) Dg(t_0) D g ( t 0 )
Exemplo Considerando
P = { ( x , y , z ) ∈ R 3 : z = x 2 + y 2 , z < 1 } P = \{(x,y,z) \in \R^3: z = x^2+y^2, z < 1\} P = {( x , y , z ) ∈ R 3 : z = x 2 + y 2 , z < 1 } Escrevendo a sua parametrização, recorrendo às coordenadas cilíndricas:
g ( ρ , θ ) = ( ρ cos θ , ρ sin θ , ρ 2 ) g(\rho, \theta) = (\rho \cos \theta, \rho \sin \theta, \rho^2) g ( ρ , θ ) = ( ρ cos θ , ρ sin θ , ρ 2 ) Qual o espaço tangente e normal em ( 1 2 , 1 2 , 1 2 ) (\frac{1}{2}, \frac{1}{2},\frac{1}{2}) ( 2 1 , 2 1 , 2 1 )
Logo g ( 2 2 , π 4 ) = ( 1 2 , 1 2 , 1 2 ) g\left(\frac{\sqrt{2}}{2}, \frac{\pi}{4}\right) = \left(\frac{1}{2},\frac{1}{2},\frac{1}{2}\right) g ( 2 2 , 4 π ) = ( 2 1 , 2 1 , 2 1 )
D g ( ρ , θ ) = [ cos θ − ρ sin θ sin θ ρ cos θ 2 ρ 0 ] Dg(\rho, \theta) = \begin{bmatrix}
\cos \theta & -\rho \sin \theta\\
\sin \theta & \rho \cos \theta\\
2\rho & 0
\end{bmatrix} D g ( ρ , θ ) = cos θ sin θ 2 ρ − ρ sin θ ρ cos θ 0 No ponto ( 2 2 , π 4 ) \left(\frac{\sqrt{2}}{2}, \frac{\pi}{4}\right) ( 2 2 , 4 π )
D g ( 2 2 , π 4 ) = [ 2 2 − 1 2 2 2 1 2 2 0 ] Dg\left(\frac{\sqrt{2}}{2}, \frac{\pi}{4}\right) = \begin{bmatrix}
\frac{\sqrt{2}}{2} & -\frac{1}{2}\\
\frac{\sqrt{2}}{2} & \frac{1}{2}\\
\sqrt{2} & 0
\end{bmatrix} D g ( 2 2 , 4 π ) = 2 2 2 2 2 − 2 1 2 1 0 Temos assim o espaço tangente:
T ( 1 2 , 1 2 , 1 2 ) P = L { ( 2 2 , 2 2 , 2 ) , ( − 1 2 , 1 2 , 0 ) } T_{(\frac{1}{2}, \frac{1}{2},\frac{1}{2})}P=
\mathcal{L} \left\{\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}, \sqrt{2}\right), \left(-\frac{1}{2}, \frac{1}{2}, 0\right)\right\} T ( 2 1 , 2 1 , 2 1 ) P = L { ( 2 2 , 2 2 , 2 ) , ( − 2 1 , 2 1 , 0 ) } Para calcular o espaço normal, fazemos:
{ ( x , y , z ) ⋅ ( 2 2 , 2 2 , 2 ) = 0 ( x , y , z ) ⋅ ( − 1 2 , 1 2 , 0 ) = 0 ⇒ { 2 2 x + 2 2 y + 2 z = 0 − 1 2 x + 1 2 y = 0 ⇒ ⇒ { x + y + 2 z = 0 x = y ⇒ { x = − z x = y \begin{darray}{cc}
\begin{cases}
(x,y,z)\cdot\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}, \sqrt{2}\right) = 0\\
(x,y,z)\cdot\left(-\frac{1}{2}, \frac{1}{2}, 0\right) = 0
\end{cases}
\Rightarrow
\begin{cases}
\frac{\sqrt{2}}{2} x + \frac{\sqrt{2}}{2} y + \sqrt{2} z = 0\\
-\frac{1}{2} x + \frac{1}{2} y = 0
\end{cases}
\Rightarrow\\
\Rightarrow
\begin{cases}
x+y+2z = 0\\
x = y
\end{cases}
\Rightarrow
\begin{cases}
x = -z\\
x = y
\end{cases}
\end{darray} { ( x , y , z ) ⋅ ( 2 2 , 2 2 , 2 ) = 0 ( x , y , z ) ⋅ ( − 2 1 , 2 1 , 0 ) = 0 ⇒ { 2 2 x + 2 2 y + 2 z = 0 − 2 1 x + 2 1 y = 0 ⇒ ⇒ { x + y + 2 z = 0 x = y ⇒ { x = − z x = y Escolhendo um ponto que satisfaça esta condição, por exemplo ( 1 , 1 , − 1 ) (1,1,-1) ( 1 , 1 , − 1 )
( T ( 1 2 , 1 2 , 1 2 ) P ) ⊥ = L ( 1 , 1 , − 1 ) \left(T_{(\frac{1}{2}, \frac{1}{2},\frac{1}{2})}P\right)^{\perp}=
\mathcal{L} {(1,1,-1)} ( T ( 2 1 , 2 1 , 2 1 ) P ) ⊥ = L ( 1 , 1 , − 1 ) Slides: