Resumos LEIC-A
IST LEIC-AGitHub
Edit page

Cinemática a 1 Dimensão

O que é a cinemática?

A cinemática é o ramo da Física que se ocupa da descrição dos movimentos de pontos, corpos ou sistemas de corpos (grupos de objetos), sem se preocupar com a análise das suas causas.

Redução de um Corpo a um Ponto

Quando estivermos a analisar o movimento de um corpo, podemos, no geral, reduzi-lo a apenas um ponto, simplificando o problema.

Isto deve-se ao facto de que todas as partes do corpo descrevem o mesmo movimento: se tivermos um carro em movimento, tanto as portas, os bancos, o volante e mesmo o condutor movimentam-se à mesma velocidade e têm uma posição sempre igual entre si. Podemos assim, neste caso, considerar o carro como apenas um ponto e estudar o movimento desse ponto.

Ao ponto que resulta desta redução, chamamos ponto material.

Atenção!

Atenção que nem sempre podemos efetuar esta redução.
Por exemplo, se estivermos a estudar o movimento rotacional de um berlinde, não podemos reduzir o berlinde a um ponto.

Posição

Antes de podermos definir os conceitos abaixo, precisamos de descrever a posição atual de um corpo, em função do tempo. Assim, a posição de um corpo, já para 3 dimensões, é:

r⃗=x(t)e⃗x+y(t)e⃗y+z(t)e⃗z\vec r = x(t) \vec e_x + y(t) \vec e_y + z(t) \vec e_z

Deslocamento e Trajetória

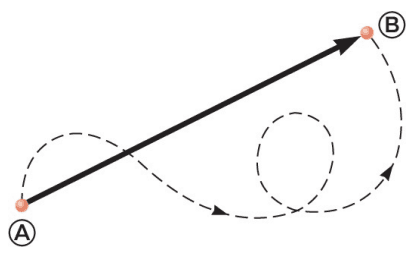
Quando um corpo se move do ponto A a um ponto B, temos:

  • Deslocamento: é o vetor que une o ponto A ao ponto B. É uma linha reta e independente do caminho.
  • Trajetória/Caminho: é o percurso que o corpo faz do ponto A ao ponto B.

Deslocamento e Caminho

O deslocamento é então dado por:

Δr⃗=r⃗2−r⃗1=Δxe⃗x+Δye⃗y+Δze⃗z\Delta \vec r = \vec r_2 - \vec r_1 = \Delta x \vec e_x + \Delta y \vec e_y + \Delta z \vec e_z

Velocidade Média

A velocidade média define-se como o quociente entre o deslocamento e o intervalo de tempo desse deslocamento.

v⃗m=Δr⃗Δt=r⃗2−r⃗1t2−t1=ΔxΔte⃗x+ΔyΔte⃗y+ΔzΔte⃗z\begin{aligned} \vec v_m &= \frac{\Delta \vec r}{\Delta t}\\ &= \frac{\vec r_2 - \vec r_1}{t_2 - t_1}\\ &= \frac{\Delta x}{\Delta t} \vec e_x + \frac{\Delta y}{\Delta t} \vec e_y + \frac{\Delta z}{\Delta t} \vec e_z \end{aligned}

Velocidade Instantânea

A velocidade instantânea é a velocidade do corpo num certo instante. Podemos pensar nisto como uma velocidade média num intervalo muito pequeno (na realidade, este é o conceito de derivada).

Assim, a velocidade instantânea é a derivada da posição:

v⃗(t)=( ⁣dx ⁣dt)e⃗x+( ⁣dy ⁣dt)e⃗y+( ⁣dz ⁣dt)e⃗z=vxe⃗x+vye⃗y+vze⃗z\begin{aligned} \vec v(t) &= \left(\frac{\d x}{\d t}\right) \vec e_x + \left(\frac{\d y}{\d t}\right) \vec e_y + \left(\frac{\d z}{\d t}\right) \vec e_z\\ &= v_x \vec e_x + v_y \vec e_y + v_z \vec e_z \end{aligned}

As unidades SI da velocidade são ms⁡−1\op{ms}^{-1}.

Aceleração Média e Instantânea

A aceleração é para a velocidade o que a velocidade é para a posição.

Assim, temos que a aceleração média é:

a⃗m=Δv⃗Δt=v⃗2−v⃗1t2−t1=ΔvxΔte⃗x+ΔvyΔte⃗y+ΔvzΔte⃗z=amxe⃗x+amye⃗y+amze⃗z\begin{aligned} \vec a_m &= \frac{\Delta \vec v}{\Delta t}\\ &= \frac{\vec v_2 - \vec v_1}{t_2 - t_1}\\ &= \frac{\Delta v_x}{\Delta t}\vec e_x + \frac{\Delta v_y}{\Delta t}\vec e_y + \frac{\Delta v_z}{\Delta t}\vec e_z\\ &= a_{mx} \vec e_x + a_{my} \vec e_y + a_{mz} \vec e_z \end{aligned}

E que a aceleração instantânea é:

a⃗(t)=( ⁣dvx ⁣dt)e⃗x+( ⁣dvy ⁣dt)e⃗y+( ⁣dvz ⁣dt)e⃗z=axe⃗x+aye⃗y+aze⃗z\begin{aligned} \vec a(t) &= \left(\frac{\d v_x}{\d t}\right) \vec e_x + \left(\frac{\d v_y}{\d t}\right) \vec e_y + \left(\frac{\d v_z}{\d t}\right) \vec e_z\\ &= a_x \vec e_x + a_y \vec e_y + a_z \vec e_z \end{aligned}

As unidades SI da aceleração são ms⁡−2\op{ms}^{-2}.

Aplicações em Situações Reais

Travagem de um Veículo

Normalmente, quando falamos de uma travagem de um veículo, existem dois momentos distintos onde podemos estudar o seu movimento:

  • Momento de reação: o condutor do veículo avistou o obstáculo e reage ao mesmo, iniciando a travagem. Ao tempo entre o avistamento do obstáculo e o início da travagem chamamos tempo de reação.
  • Momento de travagem: a travagem é iniciada e o veículo reduz a sua velocidade com aceleração constante, até ser imobilizado. A este intervalo de tempo, desde o início da travagem até à imobilização do veículo, chamamos de tempo de travagem.

Podemos observar como variam a posição, velocidade e aceleração do veículo durante estes dois momentos:

Gráficos posição, velocidade e aceleração em função do tempo

Exemplo

Um carro viaja a 45km/h⁡45 \op{km/h} numa estrada quando avista um semáforo vermelho.
O condutor do carro, após avistar o semáforo, demora 1.5s⁡1.5 \op{s} a iniciar a travagem. Ao travar, o carro é sujeito a uma aceleração de módulo 5ms⁡−25 \op{ms}^{-2}, terminando a travagem mesmo junto ao semáforo. Qual a distância do carro ao semáforo, quando o avistou?

O primeiro passo neste tipo de problemas é converter as unidades para o mais adequado. Neste caso, dá-nos mais jeito utilizar metros e segundos, pelo que temos de passar a velocidade inicial para m/s⁡\op{m/s}.

vi=45km/h⁡=12.5m/s⁡v_i = 45 \op{km/h} = 12.5 \op{m/s}

Precisamos então, para chegar à resposta do problema, de determinar a distância percorrida pelo veículo desde o momento do avistamento do obstáculo até à sua imobilização.
Dividimos assim nos dois momentos que foram referidos acima, calculando a distância percorrida em cada um deles.

  • Momento de reação

    O tempo de reação do condutor foi de tr=1.5s⁡t_r = 1.5 \op{s}, pelo que temos de calcular a distância percorrida pelo carro durante esse intervalo de tempo a 45km/h⁡45 \op{km/h}, isto é, a 12.5m/s⁡12.5 \op{m/s}.

    A equação das posições que descreve este movimento é:

    r⃗(t)=12.5t e⃗x(m⁡)\vec r(t) = 12.5t~\vec e_x\quad (\op{m})

    ou mais simplesmente, a uma dimensão,

    x(t)=12.5t(m⁡)x(t) = 12.5t\quad (\op{m})

    Assim, a distância percorrida durante o tempo de reação foi

    x(1.5)=12.5×1.5=18.75m⁡x(1.5) = 12.5 \times 1.5 = 18.75 \op{m}

  • Momento de travagem

    Neste momento já não sabemos qual foi a duração da travagem, pelo que antes de conseguirmos calcular a distância percorrida durante a travagem, temos de calcular o tempo de travagem.
    Estamos perante um movimento uniformemente retardado.

    A equação das posições que descreve este movimento é:

    r⃗(t)=(18.75+12.5t−52t2)e⃗x(m⁡)\vec r(t) = \left(18.75 + 12.5 t - \frac{5}{2} t^2\right) \vec e_x\quad (\op{m})

    ou mais simplesmente, a uma dimensão,

    x(t)=18.75+12.5t−52t2(m⁡)x(t) = 18.75 + 12.5 t - \frac{5}{2} t^2\quad (\op{m})

    É de realçar que a aceleração tem sinal negativo visto que tem sentido contrário ao movimento.

    Assim, o tempo de travagem do veículo é o tempo decorrido até à velocidade do veículo ser nula. Para isso, necessitamos da equação da velocidade deste movimento.

    vx(t)=12.5−5tv_x(t) = 12.5 - 5t

    E podemos então descobrir qual o instante em que o veículo é imobilizado.

    vx(t)=0⇔12.5−5t=0⇔t=2.5s⁡v_x(t) = 0 \Leftrightarrow 12.5 - 5t = 0 \Leftrightarrow t = 2.5 \op{s}

    Assim, o tempo de travagem é tt=2.5s⁡t_t = 2.5 \op{s}, pelo que podemos finalmente calcular a distância percorrida durante a travagem:

    x(2.5)=18.75+12.5×2.5−52×(2.5)2=34.38m⁡x(2.5) = 18.75 + 12.5 \times 2.5 - \frac{5}{2} \times (2.5)^2 = 34.38 \op{m}

Juntando a distância percorrida nos dois momentos, chegamos à distância entre o ponto de avistamento do semáforo e o semáforo:

d=18.75+34.38=53.13m⁡d = 18.75 + 34.38 = 53.13 \op{m}

Os gráficos que representam este movimento são:

Gráficos posição, velocidade e aceleração em função do tempo do exemplo

Lançamento Vertical

Quando lançamos um corpo na vertical, este descreve um movimento para cima, seguido de uma queda até ao chão.
No movimento que vamos estudar, apenas uma única força atua no corpo, a força gravítica: por simplificação, desprezamos a ação de todas as outras forças (resistência do ar, vento, etc).

Durante o movimento ascendente, a força gravítica (e consequentemente a aceleração, visto que a força resultante e a aceleração têm sempre a mesma direção/sentido, pela Segunda Lei de Newton) atua no sentido contrário ao movimento, diminuindo a velocidade do corpo.
Isto claramente corresponde à realidade, pois se atirarmos um objeto para cima ele só consegue atingir uma certa altura.

Após chegar ao ponto mais alto (altura máxima), o corpo inverte o sentido do movimento e inicia o seu movimento descendente.

No movimento descendente, o corpo aumenta a sua velocidade, visto que a aceleração tem agora o sentido do movimento. Após embater no chão, podemos ter dois casos:

  • o corpo fica no chão (por exemplo, uma bola de golfe na relva)
  • o corpo ressalta, repetindo uma ou mais vezes o movimento ascendente e descendente (por exemplo, uma bola saltitona num chão liso)

Por simplificação, a maioria dos casos estudados enquadram-se na primeira opção, podendo desprezar qualquer ressalto (geralmente temos apenas de descobrir o tempo até ao primeiro embate no chão, a altura máxima atingida, etc).

Podemos observar como variam a posição, velocidade e aceleração do corpo durante estes dois movimentos:

Gráficos posição, velocidade e aceleração em função do tempo

Exemplo

Uma bola é lançada para cima do 2º andar de um prédio, situado a 15m⁡15 \op{m} do chão, com uma velocidade inicial de 6m/s⁡6 \op{m/s}.
Considerado a aceleração gravítica g=9.8m/s⁡2g = 9.8 \op{m/s}^2 e desprezando a ação te todas as outras forças, determine o seguinte:

a) A altura máxima atingida pela bola.

A prioridade neste tipo de exercícios é definir o movimento do corpo através das equações do movimento.
Podemos considerar o sentido do eixo dos yyyy como preferirmos, mas neste caso iremos considerar o sentido positivo de baixo para cima. É indiferente, desde que seja consistente ao longo da resolução do exercício.

y(t)=15+6t−9.82t2vy(t)=6−9.8t\begin{aligned} y(t) &= 15 + 6t - \frac{9.8}{2} t^2\\ v_y(t) &= 6 - 9.8 t \end{aligned}

A bola atinge a altura máxima quando inverte o sentido do movimento, isto é, quando a sua velocidade é nula.
Como tal, o instante em que a bola está na altura máxima é dado por

vy(t)=0⇔6−9.8t=0⇔t=0.612s⁡v_y(t) = 0 \Leftrightarrow 6-9.8 t = 0 \Leftrightarrow t = 0.612 \op{s}

Podemos fazer corresponder uma posição a este instante, substituindo em y(t)y(t):

y(0.612)=15+6×0.612−9.82×(0.612)2=16.84m⁡y(0.612) = 15 + 6 \times 0.612 - \frac{9.8}{2} \times (0.612)^2 = 16.84 \op{m}

Assim, a altura máxima atingida pela bola é 16.84m⁡16.84 \op{m}, relativamente ao chão.

b) O tempo desde o lançamento até a bola embater no chão.

Para determinarmos quando tempo demora a bola a embater no chão, apenas necessitamos de determinar o instante em que a sua altura é zero.

y(t)=0⇔15+6t−9.82t2=0⇔t=−1.24s⁡ ∨ t=2.47s⁡y(t) = 0 \Leftrightarrow 15 + 6t - \frac{9.8}{2} t^2 = 0 \Leftrightarrow t = -1.24 \op{s}~\lor~t = 2.47 \op{s}

O valor negativo para o tempo não faz sentido no contexto do problema, pelo que o descartamos:

t=−1.24s⁡ ∨ t=2.47s⁡  ⟹  t=2.47s⁡\xcancel{t = -1.24 \op{s}}~\lor~t = 2.47 \op{s} \implies t = 2.47 \op{s}

Assim, a bola demora 2.47s⁡2.47 \op{s} desde o lançamento até embater no chão.

c) A velocidade com que a bola embate no chão.

Já sabemos o instante em que a bola embate no chão, pelo que temos apenas de substituir na equação da velocidade.

vy(2.47)=6−9.8×2.47=−18.21m/s⁡v_y(2.47) = 6 - 9.8 \times 2.47 = -18.21 \op{m/s}

Assim, a bola embate no chão a −18.21m/s⁡-18.21 \op{m/s}.

Os gráficos que representam este movimento são:

Gráficos posição, velocidade e aceleração em função do tempo do exemplo