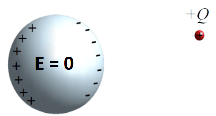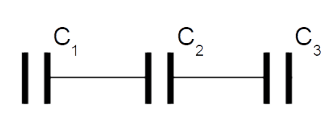Resumos LEIC-A
IST LEIC-AGitHub
Edit page

Condutores, Condensadores e Dielétricos

Os condutores que iremos estudar estarão em Eletrostática.

Condutor

Num condutor as cargas elétricas podem mover-se livremente no material.

  • Existem 2 tipos de condutores:
    • condutores metálicos onde as cargas são eletrões
    • condutores líquidos onde as cargas são iões

Dentro do Condutor

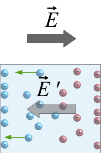
Condutor

Quando aplicamos um campo E⃗\vec E num condutor isolado, as cargas negativas (induzidas) movem-se na direção oposta ao campo E⃗\vec E, separando assim as cargas positivas das negativas.
Essas cargas induzidas criam 1 segundo campo E⃗ ′\vec E \ ' que é contrário ao campo E⃗\vec E, estes campos anulam-se e assim concluímos que o Campo Elétrico dentro do condutor é nulo.

E⃗total=0\vec E_{total} = 0

Assim pela Lei de Gauss

∇⃗⋅E⃗total=ρtotalϵ0\vec \nabla \cdot \vec E_{total} = \cfrac{\rho_{total}}{\epsilon_{0}}

Como E⃗total=0  ⟹  ρtotal=0\vec E_{total} = 0 \implies \rho_{total} = 0
Concluímos assim que a densidade de carga no interior do condutor é nula. Isto é equivalente a dizer que existe o mesmo número de cargas positivas (+)(+) e cargas negativas (−)(-), tais que as suas densidades se anulam.

  • Qualquer carga remanescente situa-se na superfície do condutor

    • Isto significa que nenhuma carga pode sair do condutor e quando interagida por um campo elétrico as cargas deslocam-se para as extremidades do condutor. Basta pensar que as cargas se deslocam para as tampas de uma caixa de Pringles

    • O Campo Elétrico E⃗⊥ \vec E \perp \ Superfície do Condutor

  • Um condutor é uma equipotencial

    • Isto é, tem o mesmo potencial em todo o seu interior.
W=Q[V(B)−V(A)]=−∫ABE⃗⋅dl⃗W = Q[V(B) - V(A)] = - \int_A^B \vec E \cdot d \vec l

Como E⃗=0\vec E = 0 e E⃗⊥dl⃗\vec E \perp d\vec l então o trabalho W=0W = 0 e V(B)=V(A)V(B) = V(A)

Cargas Induzidas

Carga

As Cargas procuram sempre o equilíbrio (E⃗=0)(\vec E = 0).

Se tivermos uma carga +Q+Q e um condutor não carregado, as cargas negativas são atraídas para a carga +Q+Q, para que assim se anule o campo no interior do condutor.

Cavidades

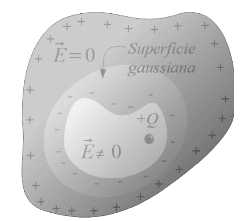
Cavidade

No caso de no interior do condutor houver uma cavidade e a carga +Q+Q estiver dentro dela, então o campo é não nulo nessa região.

Assim a carga induzida Qind Q_{ind}\ é igual a −Q-Q e a carga à superfície do condutor passa a ser positiva porque as cargas negativas aproximaram-se da carga +Q+Q deixando de estar na superfície.

No caso de não haver carga na cavidade, E⃗=0 \vec E = 0 \ na cavidade (Gaiola de Faraday)

Condensador

Um condensador é um componente que armazena cargas elétricas num campo elétrico.

Imaginemos que temos 2 condutores com carga +Q+Q e −Q-Q

Como são equipotenciais podemos calcular a sua diferença de potencial.

ΔV=V+−V−=−∫(−)(+)E⃗⋅dl⃗=E⋅d\Delta V = V_{+} - V_{-} = - \int_{(-)}^{(+)} \vec E \cdot d \vec l = E \cdot d

Para calcular o campo elétrico de cada condutor seria algo muito difícil, mas sabemos uma coisa

E⃗∝Q  ⟹  V∝Q\vec E \propto Q \implies V \propto Q

∝ \propto\ significa "é proporcional a"

Assim criamos a uma constante CC de proporcionalidade chamada de Capacitância ou Capacidade

C=Q∣ΔV∣C = \cfrac{Q} {|\Delta V|}

Esta é uma grandeza geométrica que é determinada pela forma, tamanho e separação de 2 condutores.
Tem unidades SI em farad [CV][ \cfrac{C}V ] (Coulomb por Volt) Normalmente usa-se o microfarad ou o picofarad.

  • Por definição o potencial é o do condutor com carga positiva +Q+Q, e assim a capacitância é sempre maior que zero.

  • Para a capacitância de um único condutor, dizemos que o outro "condutor está no infinito e o seu campo é zero"

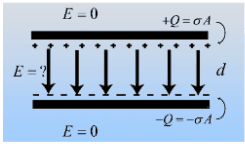
Placa

Também sabemos que para 2 placas a uma distância dd

∣ΔV∣=Ed   E=σϵ0   Q=σA|\Delta V| = E d \ \ \ E = \cfrac{\sigma}{\epsilon_{0}} \ \ \ Q = \sigma A

C=ϵ0AdC = \cfrac{\epsilon_{0} A}{d}

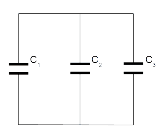
Condensadores em Paralelo

Paralelo

Se tivermos 3 Condensadores em Paralelo, as 3 placas de cima estão ao mesmo potencial assim como as debaixo, isso equivale a ter uma placa grande em cima e uma grande em baixo, e assim essa placa é a soma das 3 placas pequenas.

Assim a capacidade do Condensador é

C=Q1+Q2+Q3V=Q1V+Q2V+Q3V=C1+C2+C3C = \cfrac{Q_1+ Q_2 + Q_3}V = \cfrac{Q_1}V + \cfrac{ Q_2 }V + \cfrac{ Q_3}V = C_1 + C_2 + C_3

Condensadores em Série

Serie

Se tivermos 3 Condensadores em Série, as ligações entre todas placas tem de ser igual para manter o equilíbrio.

Assim

Q1=Q2=Q3=QQ_1 = Q_2 = Q_3 = Q

Como a diferença potencial é dada pela soma dos 3 potenciais

V1+V2+V3V_1 + V_2 + V_3

Assim a capacidade do Condensador é

C=QV1+V2+V3=1C=1C1+1C2+1C3C = \cfrac{Q}{V_1 + V_2 + V_3} = \cfrac{1}C = \cfrac {1}{ C_1 } + \cfrac {1}{ C_2 } + \cfrac {1}{ C_3 }

Trabalho

Lembrar a Definição de Trabalho

Para carregar um condensador é preciso eliminar eletrões do condutor positivo e movê-los para o condensador negativo. Isso requer trabalho pois é temos de puxar cargas negativas contra o campo elétrico.

O trabalho necessário para carregar o condensador com uma carga QQ é dado por

dW=(qC)dq  ⟹  Wq=0→Q=∫0Q(qC) dq=Q22C=CV22dW = (\cfrac{q}C) dq \implies W_{q = 0 \rightarrow Q} = \int_0^Q (\cfrac{q}C) \ dq = \cfrac{Q^2}{2C} = \cfrac{CV^2}{2}

onde qq é um carga positiva que auxilia os cálculos

Dielétricos

Com os Dielétricos entramos no estudo do campo elétrico na matéria. Existem 2 grandes grupos:

  • Condutores

    • As cargas elétricas movem-se livremente através do material

  • Dielétricos ou Isolantes

    • As cargas elétricas estão presas aos átomos ou moléculas e apenas se podem mover um pouco dentro deles
    • Existem 2 mecanismos pelos quais um campo elétrico pode distorcer a distribuição de carga de um átomo ou molécula dielétrica
      • Estiramento
      • Rotação

Quando estes mecanismos acontecem dizemos que o átomo está Polarizado.

Isolante no Meio de um Condensador

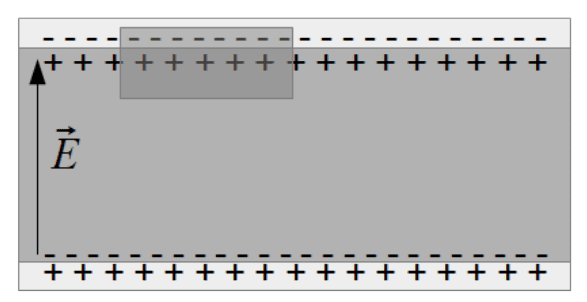
Burguer

Imaginemos que colocamos um isolante entre 2 placas de 1 condensador.

Se o isolante tocar simultaneamente nas duas placas, a capacitância aumenta por um fator kk

kk é assim a constante dielétrica do meio, no vácuo k=1k = 1.

Isto acontece porque como vimos antes a Capacitância sem a presença do dielétrico é dada por

C=ϵ0Aδ , C=Q∣ΔV∣C = \cfrac{\epsilon_{0}A}{\delta} \ , \ C = \cfrac{Q}{| \Delta V|}

onde AA é a área das placas e δ\delta a distância entre elas.

Se a Capacitância aumentar CC, para a mesma carga QQ a diferença de potencial VV é menor.

Se a diferença de potencial VV é menor, então o campo elétrico EE é também menor.

Assim podemos concluir que na parte superior do condensador irão haver cargas positivas e na parte inferior do condensador irão haver cargas negativas.

Momento Dipolar por Unidade de Volume

Isto leva nos a dizer que se houver N átomos por unidade de volume haverá momento dipolar por unidade de volume

P⃗=Np⃗\vec P = N \vec p

O P⃗\vec P pode mudar de ponto para ponto mas em cada ponto P⃗∝E⃗\vec P \propto \vec E

Consideremos uma superfície dipolar com um certo momento dipolar por unidade de volume. Haverá uma densidade de carga produzida por ela? Não se P⃗\vec P for uniforme.

Se as cargas que foram deslocadas têm a mesma densidade média não teremos uma carga líquida no volume.

Se P⃗\vec P fosse maior num lugar do que noutro então mais carga seria movida para dentro de 1 determinada região do que noutra e teríamos uma densidade de carga no volume.

No condutor de placas paralelas vamos supor que P⃗\vec P é uniforme e por isso só nos precisamos de preocupar com o que se passa nas superfícies.
Na superfície de baixo haverá uma distribuição superficial de carga negativa (chamada carga superficial de polarização) com a correspondente carga positiva a uma distância d=pQd = \cfrac{p}Q acima,
enquanto na superfície de cima acontecerá o fenómeno inverso.

Vamos assumir que p⃗⊥\vec p \perp superfície.

O número de dipolos que aparecem na superfície de baixo é dado pelo número de dipolos por unidade de volume NN multiplicados pelo volume de uma camada de superfície AA de altura dd. Em cada dipolo há uma carga eletrónica qeq_e e por isso a carga total é A⋅N⋅d⋅qeA \cdot N \cdot d \cdot q_e
Assim a densidade de carga superficial σpol\sigma_{pol} é

σpol=A⋅N⋅d⋅qeA=N d qe=P\sigma_{pol} = \cfrac{A \cdot N \cdot d \cdot q_e}A = N \ d \ q_e = P

As placas dos condutores também têm uma densidade de carga σpc\sigma_{pc}.

As cargas de polarização só existem porque existe σpc\sigma_{pc}.

Se descarregarmos o condensador, σpc\sigma_{pc} desaparece porque os dipolos desaparecem por ausência de campo aplicado e não por serem transportados pelo fio de terra.

Constante Dielétrica

Dentro do dielétrico

E=σpc−σpolϵ0=σpc−Pϵ0E = \cfrac{\sigma_{pc} - \sigma_{pol}}{\epsilon_0} = \cfrac{\sigma_{pc} - P}{\epsilon_0}

Como sabemos que P⃗∝E⃗\vec P \propto \vec E podemos escrever que

P⃗=χϵ0E⃗\vec P = \chi \epsilon_0 \vec E

χ\chi é a constante de suscetibilidade elétrica do dielétrico

E=σpcϵ011+χE = \cfrac{\sigma_{pc}}{\epsilon_0} \cfrac{1}{1+ \chi}

11+χ\cfrac{1}{1+ \chi} diz-nos quanto o campo diminui no interior do dielétrico

A diferença de potencial entre as placas é o integral de campo elétrico. Como o campo é uniforme e a carga total no condensador é σpc A\sigma_{pc} \ A

V=Eδ=E=σpcϵ0δ1+χC=ϵ0Aσ(1+χ)  ⟹  k=1+χV = E\delta = E = \cfrac{\sigma_{pc}}{\epsilon_0} \cfrac{\delta}{1+ \chi}\\ C = \cfrac{\epsilon_0A}{\sigma}(1+\chi) \implies k = 1 + \chi

kk - Constante Dielétrica

Se a polarização P⃗\vec P não for uniforme,

A carga total σpol\sigma_{pol} por unidade de volume que atravessou a superfície é

σpol=P⃗⋅n⃗\sigma_{pol} = \vec P \cdot \vec n

E a densidade de carga ρpol\rho_{pol} é

ρpol=−∇⃗⋅P⃗\rho_{pol} = -\vec \nabla \cdot \vec P

Polarização

Como sabemos da Eletrostática

∇⃗⋅E⃗=ρϵ0      ∇⃗×E⃗=0\vec \nabla \cdot \vec E = \cfrac{\rho}{\epsilon_{0}} \ \ \ \ \ \ \vec \nabla \times \vec E = 0

onde ρ\rho é a densidade de todas as cargas.

No entanto num condutor existem cargas livres e cargas polarizadas, cada uma delas com a sua densidade de carga.

∇⃗⋅E⃗=ρlivre+ρpolϵ0\vec \nabla \cdot \vec E = \cfrac{\rho_{livre} + \rho_{pol}}{\epsilon_{0}}

Mas sabemos que

ρpol=−∇⃗⋅P⃗\rho_{pol} = -\vec \nabla \cdot \vec P
P⃗=χϵ0E⃗\vec P = \chi \epsilon_0 \vec E
k=1+χk = 1 + \chi

Então

∇⃗⋅E⃗=ρlivre−∇⃗⋅P⃗ϵ0  ⟹  ∇⃗(E⃗+P⃗ϵ0)=ρlivreϵ0\vec \nabla \cdot \vec E = \cfrac{\rho_{livre} -\vec \nabla \cdot \vec P}{\epsilon_{0}} \implies \vec \nabla (\vec E + \cfrac{\vec P}{\epsilon_{0}}) = \cfrac{\rho_{livre}}{\epsilon_{0}}
∇⃗[(1+χ)E⃗]=∇⃗(kE⃗)=ρlivreϵ0\vec \nabla [(1 + \chi) \vec E ] = \vec \nabla (k \vec E) = \cfrac{\rho_{livre}}{\epsilon_{0}}

kk encontra-se dentro da divergência, isso deve-se ao seu valor variar de ponto para ponto.

Deslocamento Elétrico

Para combinar o Campo Elétrico e a Polarização utiliza-se o Deslocamento Elétrico DD
O Deslocamento Elétrico tenta descrever as propriedades da matéria (nos dielétricos lineares)

D⃗=ϵ0E⃗+P⃗\vec D = \epsilon_{0} \vec E + \vec P

Assim podemos escrever

∇⃗⋅D⃗=ρlivre\vec \nabla \cdot \vec D = \rho_{livre}\\
∇⃗×D⃗=∇⃗×P⃗ \vec \nabla \times \vec D = \vec \nabla \times \vec P\\
∮SD⃗⋅dS⃗=Qlivre \oint_S \vec D \cdot d \vec S = Q_{livre}
D⃗=ϵ0(1+χ)E⃗=kϵ0E⃗  ⟺  D⃗=ϵE⃗\vec D = \epsilon_{0}(1 + \chi)\vec E = k \epsilon_{0} \vec E \iff \vec D = \epsilon \vec E

ϵ=kϵ0\epsilon = k \epsilon_{0} é a permitividade do meio

E podemos concluir que

D+⊥−D−⊥=ρlivreD+∥−D−∥=P+∥−P−∥D_{+}^{\perp} - D_{-}^{\perp} = \rho_{livre}\\ D_{+}^{\parallel} - D_{-}^{\parallel} = P_{+}^{\parallel} - P_{-}^{\parallel}

++ e −- indica acima e abaixo da superfície respetivamente.

Num dielétrico linear homogéneo a densidade (volumétrica) de cargas de polarização ρpol\rho_{pol} é proporcional à densidade (volumétrica) de cargas livres ρlivre\rho_{livre}

ρpol=−∇⃗⋅P⃗=−(χ1+χ)∇⃗⋅D⃗=−(χ1+χ)ρlivre\rho_{pol} = - \vec \nabla \cdot \vec P = - (\cfrac{\chi}{1+ \chi}) \vec \nabla \cdot \vec D = - (\cfrac{\chi}{1+ \chi})\rho_{livre}

Em particular, a menos que existam cargas livres inseridas no dielétrico ρpol=0\rho_{pol} = 0 e toda a carga tem de estar na superfície. As condições fronteira podem ser escritas na forma

ϵ+E+⊥−ϵ−E−⊥=σlivre\epsilon_{+} E_{+}^{\perp} - \epsilon_{-} E_{-}^{\perp} = \sigma_{livre}

Slides: