Um campo (ϕ \phi ϕ
Essa quantidade pode ser escalar ou vetorial.
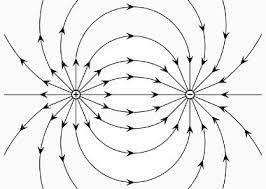
Por exemplo, o campo gravítico é um campo vetorial (ϕ ⃗ : R 3 → R 3 \vec \phi: \mathbb{R}^3 \to \mathbb{R}^3 ϕ : R 3 → R 3
ϕ ⃗ ( r ⃗ ) = − G M r 2 e ⃗ r \vec\phi (\vec r) = -G\cfrac{M}{r^2} \vec e_r ϕ ( r ) = − G r 2 M e r Para saber como um campo escalar varia com a posição temos de calcular o seu Gradiente
∇ ⃗ ϕ ( r ⃗ ) = ∂ ϕ ∂ x 1 e ⃗ 1 + ∂ ϕ ∂ x 2 e ⃗ 2 + ∂ ϕ ∂ x 3 e ⃗ 3 = ∑ i = 1 3 ∂ ϕ ∂ x i e ⃗ i = ( ∂ ϕ ∂ x 1 , ∂ ϕ ∂ x 2 , ∂ ϕ ∂ x 3 ) \vec\nabla \phi(\vec r) = \cfrac{\partial \phi}{\partial x_1}\vec e_1 + \cfrac{\partial \phi}{\partial x_2}\vec e_2 + \cfrac{\partial \phi}{\partial x_3}\vec e_3 = \sum\limits_{i =1}^{3} \dfrac {\partial \phi}{\partial x_i}\vec e_i = (\frac{\partial \phi}{\partial x_1}, \frac{\partial \phi}{\partial x_2}, \frac{\partial \phi}{\partial x_3}) ∇ ϕ ( r ) = ∂ x 1 ∂ ϕ e 1 + ∂ x 2 ∂ ϕ e 2 + ∂ x 3 ∂ ϕ e 3 = i = 1 ∑ 3 ∂ x i ∂ ϕ e i = ( ∂ x 1 ∂ ϕ , ∂ x 2 ∂ ϕ , ∂ x 3 ∂ ϕ ) Geometricamente a maior variação de ϕ \phi ϕ ∇ ⃗ ϕ \vec\nabla \phi ∇ ϕ d l ⃗ d \vec l d l ∣ d l ⃗ ∣ |d\vec l| ∣ d l ∣
d ϕ = ∑ i = 1 3 ∂ ϕ ∂ x i d x i = ∇ ⃗ ϕ ⋅ d l ⃗ = ∣ ∇ ⃗ ϕ ∣ ∣ d l ⃗ ∣ cos ( ∇ ⃗ ϕ , d l ⃗ ) d \phi = \sum\limits_{i =1}^{3} \dfrac {\partial \phi}{\partial x_i} dx_i
= \vec\nabla \phi \cdot d \vec l
= |\vec\nabla \phi| \ |d \vec l|\ \cos(\vec\nabla \phi,d \vec l) d ϕ = i = 1 ∑ 3 ∂ x i ∂ ϕ d x i = ∇ ϕ ⋅ d l = ∣ ∇ ϕ ∣ ∣ d l ∣ cos ( ∇ ϕ , d l ) ∇ ⃗ ϕ \vec\nabla \phi ∇ ϕ ϕ \phi ϕ ∇ ⃗ ϕ \vec\nabla \phi ∇ ϕ
O operador ∇ ⃗ \vec \nabla ∇ ∇ ⃗ = ∑ i = 1 n ∂ ∂ x i e i ⃗ \vec \nabla = \sum_{i=1}^n\frac{\partial}{\partial x_i}\vec{e_i} ∇ = ∑ i = 1 n ∂ x i ∂ e i
Se a quantidade (ϕ ⃗ ( r ⃗ ) \vec\phi(\vec r) ϕ ( r ) ∇ ⃗ \vec\nabla ∇
∇ ⃗ ⋅ ϕ ( r ⃗ ) = ∑ i = 1 3 ∂ ϕ i ∂ x i \vec\nabla \cdot \phi(\vec r) = \sum_{i=1}^3 \frac{\partial \phi_i}{\partial x_i} ∇ ⋅ ϕ ( r ) = i = 1 ∑ 3 ∂ x i ∂ ϕ i O resultado será um número.
∇ ⃗ × ϕ ( r ⃗ ) = ( ∂ ϕ 2 ∂ x 3 − ∂ ϕ 3 ∂ x 2 , ∂ ϕ 3 ∂ x 1 − ∂ ϕ 1 ∂ x 3 , ∂ ϕ 1 ∂ x 2 − ∂ ϕ 2 ∂ x 1 ) \vec\nabla \times \phi(\vec r) = (\frac{\partial \phi_2}{\partial x_3} - \frac{\partial \phi_3}{\partial x_2}, \frac{\partial \phi_3}{\partial x_1} - \frac{\partial \phi_1}{\partial x_3}, \frac{\partial \phi_1}{\partial x_2} - \frac{\partial \phi_2}{\partial x_1}) ∇ × ϕ ( r ) = ( ∂ x 3 ∂ ϕ 2 − ∂ x 2 ∂ ϕ 3 , ∂ x 1 ∂ ϕ 3 − ∂ x 3 ∂ ϕ 1 , ∂ x 2 ∂ ϕ 1 − ∂ x 1 ∂ ϕ 2 ) O resultado será um (pseudo-)vetor, isto porque para dois vetores a ⃗ \vec a a b ⃗ \vec b b a ⃗ × b ⃗ \vec a \times \vec b a × b − a ⃗ × − b ⃗ - \vec a \times - \vec b − a × − b
Para ϕ i \phi _i ϕ i
ϕ ( r ⃗ ) = ∑ i = 1 3 ϕ i e ⃗ i = ( ϕ 1 , ϕ 2 , ϕ 3 ) ∇ ⃗ ⋅ ϕ ( r ⃗ ) = 0 ∇ ⃗ × ϕ ( r ⃗ ) = 0 \begin{darray}{c}
\phi(\vec r) = \sum\limits_{i =1}^{3} \phi_i \vec e_i = (\phi_1, \phi_2, \phi_3)\\
\vec\nabla \cdot \phi(\vec r) = 0\\
\vec\nabla \times \phi(\vec r) = 0
\end{darray} ϕ ( r ) = i = 1 ∑ 3 ϕ i e i = ( ϕ 1 , ϕ 2 , ϕ 3 ) ∇ ⋅ ϕ ( r ) = 0 ∇ × ϕ ( r ) = 0
Com A A A
ϕ ( r ⃗ ) = ∑ i = 1 3 A x i e ⃗ i = ( A x 1 , A x 2 , A x 3 ) ∇ ⃗ ⋅ ϕ ( r ⃗ ) = 3 A ∇ ⃗ × ϕ ( r ⃗ ) = 0 \begin{darray}{c}
\phi(\vec r) = \sum\limits_{i =1}^{3} Ax_i \vec e_i = (Ax_1, Ax_2, Ax_3)\\
\vec\nabla \cdot \phi(\vec r) = 3A\\
\vec\nabla \times \phi(\vec r) = 0
\end{darray} ϕ ( r ) = i = 1 ∑ 3 A x i e i = ( A x 1 , A x 2 , A x 3 ) ∇ ⋅ ϕ ( r ) = 3 A ∇ × ϕ ( r ) = 0
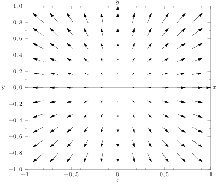
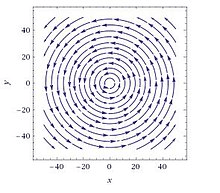
Com ϕ 1 ( r ⃗ ) = x 2 x 3 , ϕ 2 ( r ⃗ ) = − x 1 x 3 , ϕ 3 ( r ⃗ ) = 0 \phi _1(\vec r) = \cfrac{x_2}{x_3},\ \phi _2(\vec r) = -\cfrac{x_1}{x_3},\ \phi _3(\vec r) = 0 ϕ 1 ( r ) = x 3 x 2 , ϕ 2 ( r ) = − x 3 x 1 , ϕ 3 ( r ) = 0
ϕ ( r ⃗ ) = ∑ i = 1 3 ϕ i ( r ⃗ ) e ⃗ i = ( x 2 x 3 , − x 1 x 3 , 0 ) \phi(\vec r) = \sum\limits_{i =1}^{3} \phi_i (\vec r) \vec e_i = (\frac{x_2}{x_3}, -\frac{x_1}{x_3}, 0) ϕ ( r ) = i = 1 ∑ 3 ϕ i ( r ) e i = ( x 3 x 2 , − x 3 x 1 , 0 ) ∇ ⃗ ⋅ ϕ ( r ⃗ ) = 0 ∇ ⃗ × ϕ ( r ⃗ ) = − x 1 e ⃗ 1 + x 2 e ⃗ 2 + x 3 e ⃗ 3 x 3 2 \begin{darray}{c}
\vec\nabla \cdot \phi(\vec r) = 0 &&
\vec\nabla \times \phi(\vec r) = - \cfrac{x_1\vec e_1 + x_2\vec e_2+ x_3\vec e_3 }{x_3 ^2}
\end{darray} ∇ ⋅ ϕ ( r ) = 0 ∇ × ϕ ( r ) = − x 3 2 x 1 e 1 + x 2 e 2 + x 3 e 3
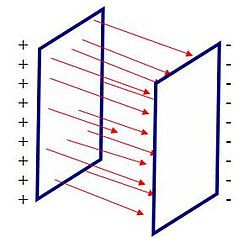
Uma linha de campo é uma curva tal que em cada ponto o
campo é tangente à curva.→ \rightarrow →
δ \delta δ A função de Dirac é uma função que em que é nula em todo o seu domínio exceto num único ponto em que tem o valor infinito.
δ ( x − a ) = { 0 , se x ≠ a ∞ , se x = a \delta (x-a) =
\begin{cases}
0,\text{ se }x \neq a\\
\infty ,\text{ se }x = a
\end{cases} δ ( x − a ) = { 0 , se x = a ∞ , se x = a ∫ − ∞ ∞ δ ( x − a ) d x = 1 \int^\infty_{-\infty} \delta (x-a) \d x = 1 ∫ − ∞ ∞ δ ( x − a ) d x = 1 Se tivermos um campo ϕ ⃗ \vec \phi ϕ
∇ ⃗ ⋅ ϕ ⃗ = f , \vec \nabla \cdot \vec \phi = f, ∇ ⋅ ϕ = f , ∇ ⃗ × ϕ ⃗ = Θ ⃗ , ( ⟹ ∇ ⃗ ⋅ Θ ⃗ = 0 ) \vec \nabla \times \vec \phi = \vec \Theta, (\implies \vec \nabla \cdot \vec \Theta = 0) ∇ × ϕ = Θ , ( ⟹ ∇ ⋅ Θ = 0 ) em que f f f Θ ⃗ \vec \Theta Θ
É impossível calcular ϕ ⃗ \vec \phi ϕ ∞ \infty ∞
Se ∇ ⃗ × ϕ ⃗ = 0 \vec \nabla \times \vec \phi = 0 ∇ × ϕ = 0
ϕ ⃗ = − ∇ ⃗ V \vec \phi = - \vec\nabla V ϕ = − ∇ V Onde V V V
Assim, ∫ A B ϕ ⃗ d r ⃗ \int^B_A \vec \phi \d \vec r ∫ A B ϕ d r A A A B B B
Se ∇ ⃗ ⋅ ϕ ⃗ = 0 \vec \nabla \cdot \vec \phi = 0 ∇ ⋅ ϕ = 0
ϕ ⃗ = ∇ ⃗ × A ⃗ \vec \phi = \vec\nabla \times \vec A ϕ = ∇ × A
Onde A ⃗ \vec A A
Assim, ∫ ϕ ⃗ d S ⃗ \int \vec \phi \d\vec S ∫ ϕ d S
Qualquer campo pode ser escrito na forma ϕ ⃗ = − ∇ ⃗ V + ∇ ⃗ × A ⃗ \vec \phi = - \vec\nabla V + \vec\nabla \times \vec A ϕ = − ∇ V + ∇ × A
Slides: