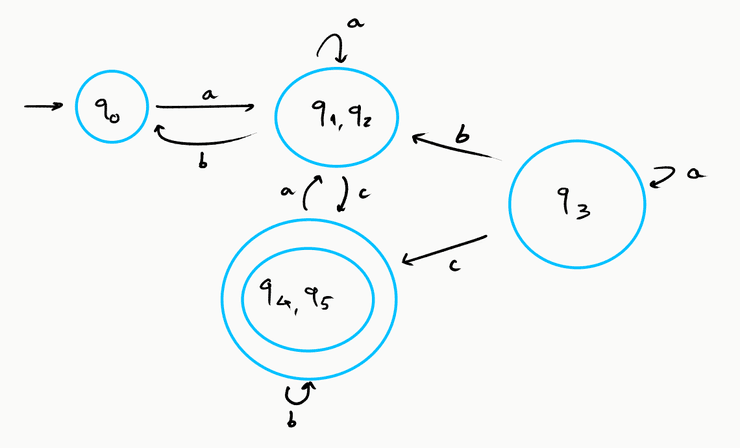Linguagens e Autómatos
Alfabetos, Palavras e Linguagens
Definimos um alfabeto como um conjunto finito não-vazio (de símbolos). Um alfabeto costuma ser representado pela letra grega .
Exemplo de Alfabeto
Um exemplo de um alfabeto é o conjunto
Definimos uma palavra sobre um alfabeto como uma sequência finita de elementos de . O conjunto de todas as palavras constituídas pelos símbolos do alfabeto é representado por .
Existe uma palavra, a que chamamos palavra vazia e representamos por que satisfaz para qualquer alfabeto .
Exemplo de Palavra
O conjunto de palavras sobre o alfabeto contém, por exemplo, as palavras . Contudo, não contém as palavras , , .
Nota
Para um alfabeto com elementos, o número de palavras de tamanho sobre esse alfabeto é .
Nomeadamente, a única () palavra de tamanho é a palavra vazia .
Operações sobre palavras
Para uma palavra definimos a operação como a operação de reversão da palavra.
Por exemplo, para , temos que .
Definimos ainda a operação binária de concatenação .
Por exemplo, para e temos que .
Temos nomeadamente que, .
Note-se que esta operação não é comutativa, mas é associativa.
Para , denotamos por à palavra que resulta da concatenação de consigo própria vezes. Mais precisamente,
Usamos ainda a notação para representar o comprimento da palavra .
Por exemplo, e .
Para qualquer , usamos para nos referir ao -ésimo símbolo da palavra .
Por exemplo, para tem-se que , e .
Uma linguagem sobre o alfabeto é qualquer conjunto .
Operações sobre Linguagens
Damos o nome de linguagem complementar de à linguagem .
Denotamos por o conjunto de todas as linguagens sobre .
Dadas duas linguagens , definimos a concatenação das linguagens como sendo a linguagem .
Definimos ainda o fecho de Kleene de uma linguagem à linguagem
Exemplo de Linguagem
Um exemplo de uma linguagem sobre o alfabeto é as palavras que acabam com exatamente três 's.
As linguagens no sentido mais corrente da palavra (Português, Inglês, Mandarim) ou mesmo as linguagens de programação são linguagens de acordo com esta definição. Têm um alfabeto (no caso do português, corresponde às letras - minúsculas, maiúsculas, acentuadas e não acentuadas -, bem como outros símbolos - !, ?, ., por exemplo) que, quando de acordo com uma regra (muito complexa, claro) formam palavras "aceites", isto é, palavras que estão de acordo com as regras da linguagem.
Autómatos
Autómatos Finitos Determinísticos
Um autómato finito determinístico (AFD) é definido como um quíntuplo tal que
- é um alfabeto;
- é um conjunto finito não vazio de estados;
- é o estado inicial;
- é um conjunto de estados finais;
- é uma função de transição.
Cada AFD define uma linguagem sobre o seu alfabeto .
Dizemos que um autómato é total se a função de transição estiver definida para todo o elemento em , isto é, se a função de transição em cada estado estiver definida para todas as letras.
Um autómato não total pode ser convertido num autómato total da seguinte forma:
- adiciona-se um estado não final ;
- estende-se a função de transição tal que para todo o par tal que a função de transição não fosse definida;
- define-se , para todo o . É conveniente pensar neste estado como um "estado lixo".
Para um AFD definimos a função de transição estendida deste autómato como a função tal que
para cada , e .
Entenda-se esta função como a função que, dado um estado inicial e uma palavra, devolve o estado que resulta da aplicação da função de transição do autómato às sucessivas letras da palavra.
Dizemos que uma palavra é aceite por um AFD se .
Ao conjunto das palavras aceites por um AFD , damos o nome de linguagem reconhecida por esse AFD.
Grafos de AFD's
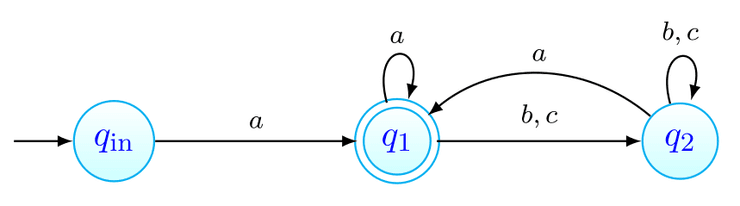
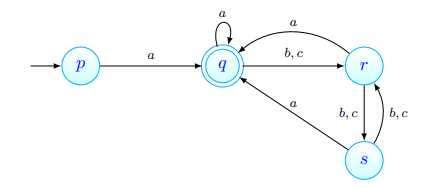
Estas entidades são normalmente representadas e entendidas de acordo com grafos como o que mostramos abaixo. Para caracterizar rigorosamente esta linguagem é útil considerar a extensão a da função de transição do AFD.
Este gráfico representa o autómato cujo:
- alfabeto é
- conjunto de estados é ;
- estado inicial é ;
- conjunto de estados finais é ;
- função de transição é tal que
Mais genericamente, a representação gráfica de um autómato é tal que:
- os estados correspondem aos vértices do grafo;
- o estado inicial é aquele em que entra a seta sem origem ;
- os estados finais são os rodeados;
- as arestas (dirigidas) indicam a definição da função .
Uma linguagem diz-se regular se existe um AFD com alfabeto tal que . Ou seja, uma linguagem é regular se for reconhecida por um AFD. Denota-se por o conjunto de todas as linguagens regulares com alfabeto .
Usa-se apenas em vez de sempre que o alfabeto esteja subentendido ou não seja importante o contexto.
Equivalência e Minimização de AFD's
Dizemos que dois AFD's são equivalentes se reconhecerem a mesma linguagem.
Para estudar a equivalência de AFD's, introduzimos as seguintes definições:
Para um AFD dizemos que um estado é:
- acessível se existe tal que . Por outras palavras, um estado é acessível se for alcançável a partir da origem;
- produtivo se existe tal que . Por outras palavras, um estado é produtivo se for possível chegar a um estado final a partir dele;
- útil se for acessível e produtivo, inútil caso contrário.
Introduzimos abaixo o algoritmo de procura de estados notáveis (APEN):
APEN
Apresentamos agora um algoritmo para a procura de estados notáveis.
O algoritmo recebe como input um AFD e dá como output um tuplo com, respetivamente, os estados acessíveis, produtivos, úteis e inúteis de .
- ;
- ;
- enquanto
- ;
- ;
Estados acessíveis determinados
- ;
- ;
- enquanto
- ;
- ;
Estados produtivos determinados
- ;
- .
Estados úteis e inúteis determinados
Temos que a execução deste algoritmo termina sempre e identifica corretamente os estados acessíveis (), produtivos (), úteis () e inúteis ().
Vamos então tentar compreender o que o algoritmo acima está a fazer:
- Numa primeira fase (passos 1 a 3), vamos descobrir quais são os estados acessíveis. Intuitivamente, podemos fazer isto começando em e fazendo uma procura (BFS) no grafo do AFD. À medida que o fazemos, colocamos esses estados no conjunto de estados acessíveis;
- Numa segunda fase (passos 4 a 6), vamos determinar os estados produtivos. Estes são aqueles que vão levar a estados finais. Então, começamos exatamente nos estados finais e fazemos também uma procura (BFS), mas desta vez no sentido contrário das setas do grafo do AFD. À medida que descobrimos os estados produtivos, colocamo-los no conjunto apropriado.
- Finalmente, determinamos os estados úteis e inúteis de acordo com a sua definição.
Para facilitar a compreensão do algoritmo, pode ser útil vê-lo em prática no exemplo seguinte.
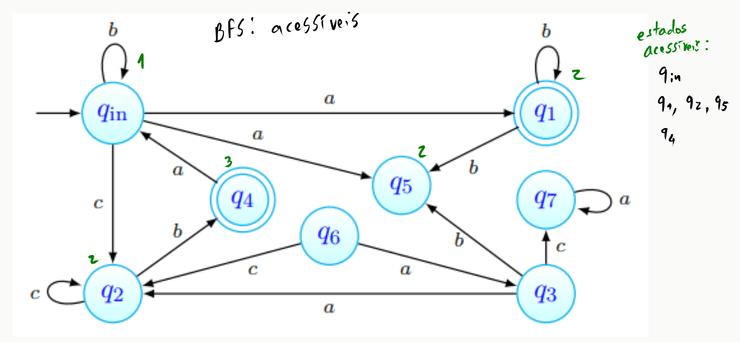
Exemplo de aplicação do APEN
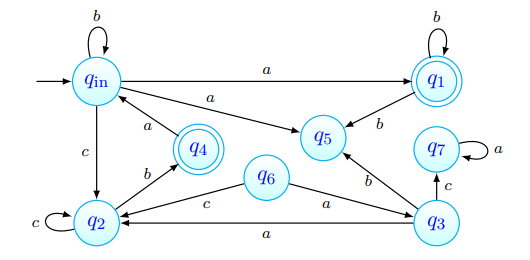
Tenhamos um AFD tal que:
Ora, procurando seguir os passos descritos na descrição acima:
-
Descobrir os estados acessíveis passa por realizar uma BFS a partir do estado inicial, - todos os estados encontrados dizem-se acessíveis:
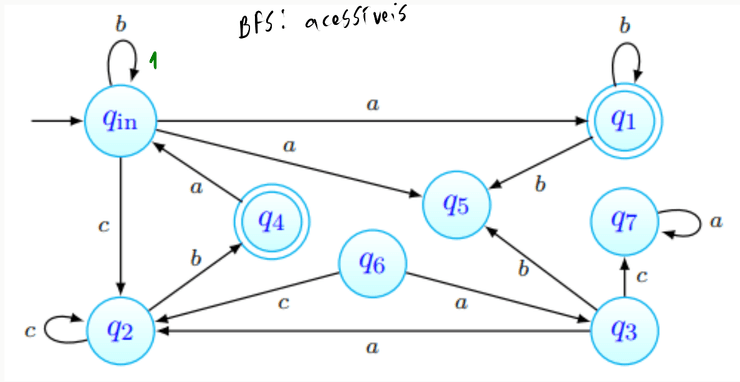
Começamos com o conjunto de estados acessíveis a conter apenas :
Logo de seguida, começamos a BFS partindo desse mesmo estado:
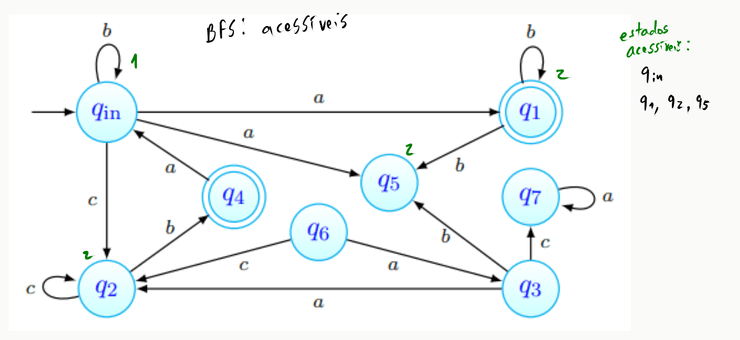
Encontrámos, a distância do estado inicial, os estados . A BFS continua então, partindo desses mesmos estados, tal que:
Podemos observar que a procura encontrou aqui . Mais ainda, temos que não há mais caminhos por onde prosseguir. A procura termina, portanto, e o conjunto de estados acessíveis foi obtido.
-
De seguida, determinar os estados produtivos: fazer BFS's, partindo de cada estado final, pelo "autómato transposto":
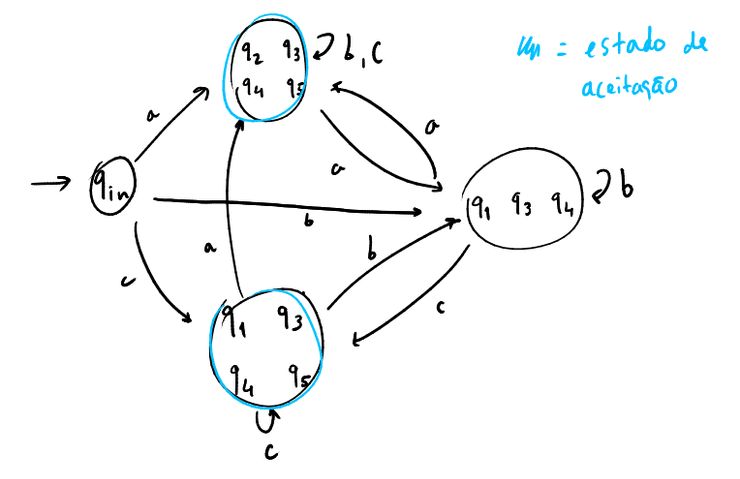
Inicialmente, o grafo transposto encontra-se assim (os estados finais estão, claro, no conjunto dos estados produtivos):
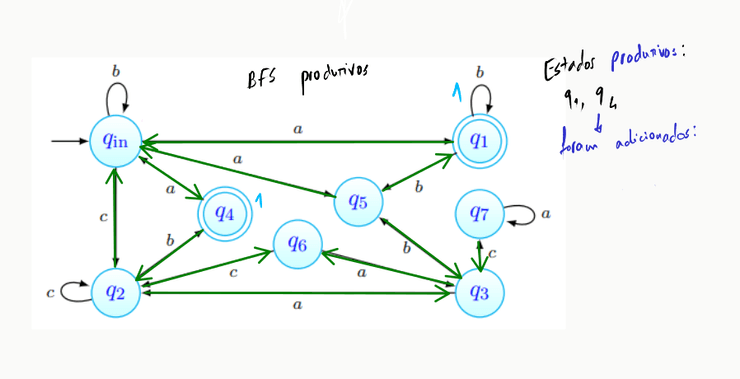
Realizamos aqui o primeiro passo da BFS - partindo dos estados finais, e , realizamos uma procura pelos estados a que podemos chegar a partir deles:
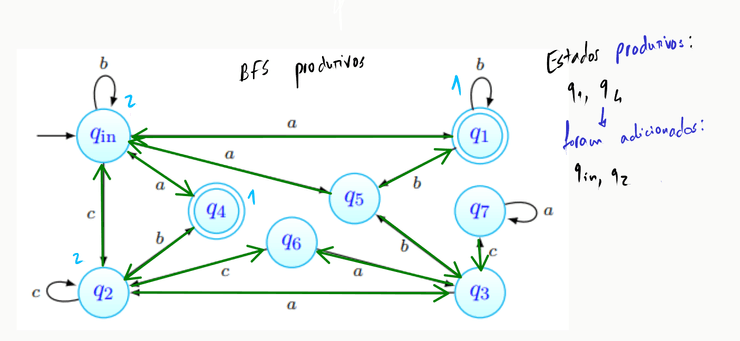
Repetimos o passo anterior, desta vez partindo dos estados que obtivemos acima: e :
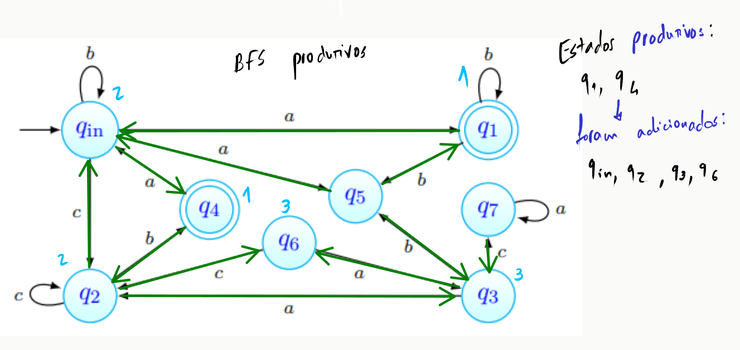
A partir dos estados acima obtidos, não podemos atingir qualquer outro estado, pelo que o algoritmo pára e temos determinado o conjunto de estados produtivos do autómato.
Ora, temos então dois conjuntos em mãos:
Pela definição da utilidade de um estado (um estado diz-se útil caso seja acessível e produtivo), podemos dizer que a interseção dos conjuntos acima corresponde ao conjunto dos estados úteis do autómato, e que portanto:
Prova da correção do algoritmo APEN
Resume-se essencialmente a: BFS funciona.
Definimos agora dois estados de um AFD como
- equivalentes se, para cada , temos que ;
- distinguíveis se não forem equivalentes. Neste caso existe pelo menos uma palavra tal que (ou vice-versa). Dizemos que distingue e ;
Vamos agora identificar critérios para distinguir estados. A partir disto, poderemos descrever um algoritmo para encontrar estados equivalentes e, consequentemente, determinar um algoritmo que minimize um AFD.
Seja um AFD e sejam e . Temos que:
- Se , e então e são distinguíveis;
- Se é produtivo e não, então e são distinguíveis;
- Se é produtivo e não está definido, então e são distinguíveis;
- Se e são estados distinguíveis, e , então e são distinguíveis. Equivalentemente, se e são equivalentes, então e também o são para qualquer ;
Ver a prova destas propriedades pode ajudar a compreendê-las.
Prova
- A palavra distingue os estados;
- Se é produtivo, existe tal que . Contudo, como não é produtivo, , pelo que a palavra distingue os estados;
- Sabemos que podemos adicionar um estado lixo ao AFD de forma que ficamos com um AFD equivalente. Se não está definido, no autómato com estado lixo vamos ver que , que é um estado não produtivo. Podemos então aplicar a condição dois a e ;
- Seja uma palavra que distingue e . Então, a palavra distingue e .
Definimos ainda como sendo o conjunto de todos os pares .
Tendo em conta estes critérios e este conjunto, introduzimos agora um algoritmo de procura de estados distinguíveis (APED).
APED
O algoritmo recebe como input o AFD e o seu output é um conjunto de pares de estados distinguíveis.
-
- ;
- enquanto e
- ;
- ;
- .
O que o algoritmo acima faz é o seguinte:
Para começar, determinar os estados distinguíveis de acordo com os 3 primeiros critérios.
Então, enquanto os houver, determinar mais estados distinguíveis de acordo com o 4º critério.
À medida que estes estados vão sendo encontrados, vão sendo agrupados no conjunto .
A execução deste algoritmo termina sempre retornando exatamente o conjunto de pares de estados distinguíveis do AFD.
Para ajudar a compreender este algoritmo pode ser útil vê-lo em prática abaixo.
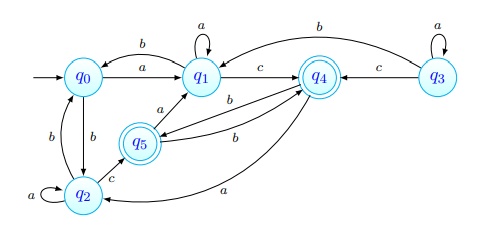
Exemplo de aplicação do APED
Consideremos um AFD tal que:
A nossa primeira tarefa será preencher segundo os três critérios iniciais:
- Num primeiro momento, organizar pares onde um elemento é um estado final e o outro é um estado não final (a ordem é irrelevante) - temos, neste momento:
-
De seguida, criar pares onde um elemento é um estado produtivo e o outro não - fazendo a BFS mencionada acima, verificamos que todos os estados são produtivos, pelo que permanece igual.
-
Por fim, encontrar todos os pares tais que um dos vértices transita, segundo um dado símbolo, para um estado produtivo, e o outro não tem qualquer transição associada a esse símbolo. Verificar esta condição pode ser mais fácil seguindo algumas heurísticas:
-
Num primeiro momento, verificar todos os estados para os quais nem todos os símbolos têm uma transição definida - aqui, não tem transição definida para e , e é o único nessa situação. Podemos a partir daqui depreender que qualquer par obtido através desta "procura" terá de envolver .
-
Obtidos símbolos sem transição definida para , aqui e , procuramos os estados que têm transição definida para os mesmos e onde essa transição leve a um estado produtivo. Neste caso, tem transições segundo e para estados produtivos, tais como e , pelo que podemos admitir que os pares criados por esta procura são .
No final destes três passos, ficamos com:
-
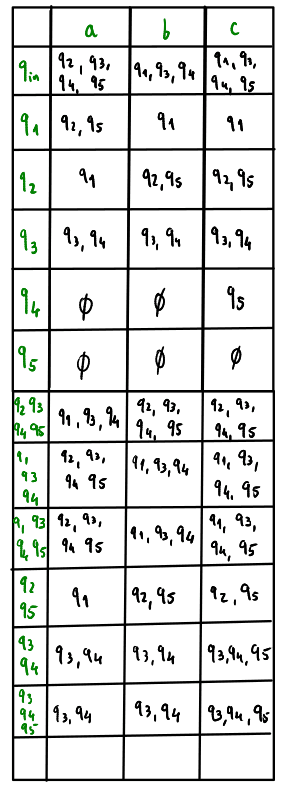
O resto do algoritmo normalmente faz-se recorrendo a uma tabela, onde cada linha e coluna correspondem a um dos estados do autómato (só se utiliza metade da tabela, já que é simétrica). A tabela corresponde ao autómato em questão seria:
Cada entrada na tabela corresponde a um dos pares de estados possíveis. Começamos por preencher a tabela com uma cruz em cada entrada que corresponde a um par em . Seria, portanto:
Entramos aqui na secção porventura mais desagradável: percorrer todos os pares de (que tenham uma cruz na tabela, portanto), e para cada um deles, verificar se existe um par que não esteja em tal que, segundo transições por um mesmo símbolo, chegam ao par de estados original (e adicionar qualquer estado encontrado à tabela). Assim que um par é (ou não) encontrado, a cruz na tabela é rodeada por um círculo (para anotar que já foi explorado).
Ora, procuremos então percorrer:
- todos os estados que incluem não adicionam pares a , já que não há qualquer estado a transitar para sequer. A tabela fica, então:
- olhando para o estado , podemos notar que não há qualquer par de estados que não esteja em e em que, segundo o mesmo símbolo, leve ao estado . Não existe qualquer estado segundo a transitar para , nem nenhum estado que segundo ou transite para , pelo que o estado dá-se por explorado sem adicionar nada de novo à tabela (sem ser circular a cruz respetiva a ).
- por fim, resta explorar . Não existe qualquer estado segundo a transitar para , nem nenhum estado que segundo ou transite para , pelo que o estado dá-se por explorado sem adicionar nada de novo à tabela (sem ser circular a cruz respetiva a ).
Todas as entradas com cruzes na tabela foram oficialmente exploradas. Os estados distinguíveis correspondem, então, às entradas com cruzes da tabela: podemos afirmar que todos os pares de estados do autómato, exceto , são distinguíveis entre si.
Além de permitir calcular o conjunto dos pares de estados distinguíveis de um AFD e, consequentemente, o conjunto dos seus pares de estados equivalentes, o APED pode também ser usado para determinar se dois AFD's e são ou não equivalentes.
Isto é feito através do algoritmo de teste à equivalência de AFD's (ATEQ):
ATEQ
O algoritmo recebe como input dois AFD's e tais que , e o seu output é um booleano que indica se os AFD's são ou não equivalentes.
- construir o AFD em que
- ;
- se
return false
caso contrárioreturn true.
Este algoritmo termina sempre, identificando como equivalentes dois AFD's se e só se eles são equivalentes.
Prova da correção do ATEQ
Verifica-se que, se , então , para qualquer .
Indutivamente, temos então que para qualquer , se , então .
Consequentemente, se para , então .
Estas propriedades verificam-se analogamente para .
Podemos inferir então que equivale a dizer que existe uma palavra tal que apenas um dos dois se verifica:
- ;
- .
consequentemente, já que e , apenas um dos dois se verifica:
- ;
- .
ou seja, a palavra é reconhecida exatamente num dos autómatos e .
Estamos agora prontos para resolver problemas de minimização de AFD's.
Um AFD diz-se mínimo se não existir nenhum outro AFD que lhe seja equivalente e tenha menos estados.
Para determinar o AFD mínimo a um AFD definimos a partição induzida pelos estados equivalentes de como o conjunto em que , para cada .
Note-se como para e distinguíveis e
, pelo que o conjunto definido é de facto uma partição.
Estamos agora em posição de introduzir o algoritmo de minimização de um AFD:
Minimização de AFD
Dado um AFD a minimização de é o AFD construído da seguinte forma:
- se , então tem apenas um estado inicial não final, e a sua função de transição não está definida para qualquer letra;
- caso contrário, em que:
- é a partição do conjunto dos estados úteis de induzida pelos estados equivalentes, com ;
- ;
- ;
- é tal que:
Observações
É relevante para o algoritmo acima notar que, para um conjunto de estados equivalentes:
-
Se existe um estado produtivo em , então só tem estados produtivos. Assim sendo, ao ignorarmos estados inúteis não podemos ignorar estados inúteis por equivalência;
-
Se , então . Isto é, se há um estado final em , todos os estados de são finais. Isto é uma consequência direta do primeiro critério de distinção de estados e faz com que a definição de estados finais de seja não ambígua;
-
Se para e , então, para cada temos que um dos dois se verifica:
- não está definido e não é produtivo;
- .
Isto faz com que a função esteja bem definida. Note-se que desta propriedade resulta que não pode oferecer dois valores diferentes, nem pode ser indefinida para alguns valores e definida para outros (uma vez que em consideramos apenas estados úteis).
Prova de equivalência de a
Seja tal que .
Se , então .
Caso contrário, para e .
Segundo o quarto critério de distinção de estados, temos que se então .
Assim sendo, por indução, temos que se , então .
Nomeadamente, uma palavra que seja aceite em , será também aceite em .
Explicado de uma forma menos rigorosa, o que estamos a constatar é que à medida que vai "lendo símbolos do alfabeto", o AFD está sempre num estado que corresponde à "classe de equivalência" do estado em que está depois de ler esses mesmos símbolos.
Ora, se ao fim dessa leitura, está num estado final, e as classes de equivalência de estados finais em são estados finais em , temos que ao fim dessa mesma leitura, também está num estado final.
Quer isto dizer que qualquer palavra aceite por é também aceite por .
Exemplo da Minimização de um AFD
Consideremos o seguinte autómato:
Apesar do decorrer do algoritmo de procura de estados distinguíveis não constar deste exemplo, consideremos que, aquando do concluir do mesmo, a tabela é tal que:
A tabela final tem, portanto, dois pares de estados equivalentes: e . Ao desenhar o autómato minimizado, os estados presentes em cada par terão de estar juntos.
Pode agora ser mais claro o porquê de considerarmos dois estados equivalentes/distinguíveis: os estados equivalentes têm, no autómato original, transições equivalentes (segundo o mesmo símbolo vão sempre para um estado num "grupo de estados equivalentes"). No caso de , por exemplo, temos que:
- através de transitam para o próprio estado em ambas as situações;
- através de transitam, em ambos os casos, para ;
- através de transitam, em ambos os casos, para um estado dentro do "par equivalente" - para e para .
Autómatos Finitos Não Determinísticos
Introduzimos a notação como o conjunto dos subconjuntos do conjunto . Também se diz que este é o conjunto das partes de .
Exemplo de um Conjunto de Partes
Temos, por exemplo, que .
Tamanho do conjunto das partes
Se um conjunto tem elementos, o conjunto tem elementos.
Prova
Isto é uma consequência de cada conjunto estar unicamente determinado pelos elementos que têm. Ora, para cada elemento, ele ou está, ou não está num dado conjunto - isto é, cada elemento tem 2 opções em relação a um dado conjunto. Sendo assim, deve haver subconjuntos de um conjunto de elementos.
Esta prova pode ser formalizada por indução.
Um autómato finito não determinístico (AFND) é definido como um quíntuplo tal que:
- é um alfabeto;
- é um conjunto finito de estados;
- é o estado inicial;
- é um conjunto de estados finais;
- é uma função de transição.
Note-se que a diferença entre um AFND e um AFD é que a função de transição num AFD não é determinística, na medida em que não define um e um só estado. Para cada par temos que define o subconjunto de dos estados que podem resultar da transição por a partir de .
Podemos ainda assinalar o autómato finito não determinístico como AFND se a função de transição tiver como domínio . Ou seja, um AFND é tal que pode haver transições que não são "causadas" por letra nenhuma. Nesta situação diz-se que o AFND tem movimentos-.
A distinção entre AFND e AFND é negligenciada em contextos que não seja relevante. Para simplificar, pode-se assumir que um AFND está sempre dotado de movimentos-.
Grafo de um AFND
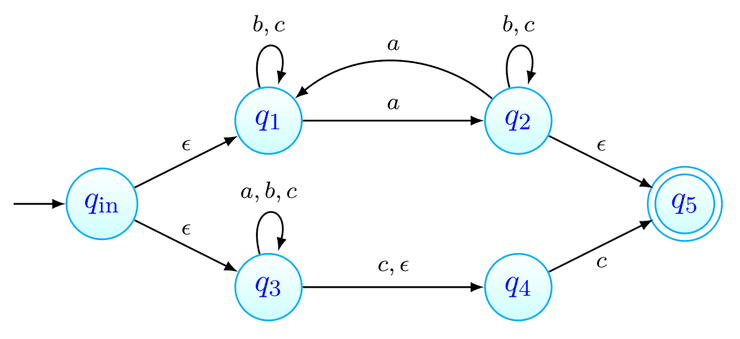
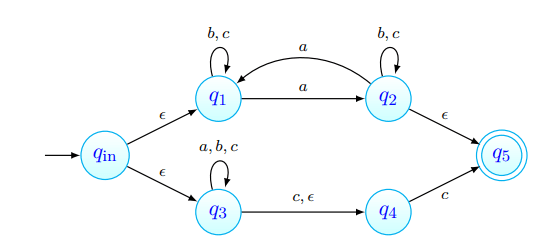
Este gráfico representa o autómato cujo:
- alfabeto é
- conjunto de estados é ;
- estado inicial é ;
- conjunto de estados finais é ;
- função de transição é tal que
Para isto, começamos por definir o fecho- de um estado.
Seja um AFND. O fecho- de um estado é o conjunto tal que:
- ;
- .
Dado um subconjunto de , o seu fecho- é o conjunto .
Dito de forma corrente, o fecho- de um estado é o conjunto de estados que se conseguem obter a partir de apenas com movimentos-.
Podemos então definir a função de transição estendida de um AFND como a função tal que, para cada , e :
Através desta função, podemos definir a palavra aceite por um AFND como qualquer palavra tal que .
Dito de forma corrente, uma palavra é aceite por um AFND se houver uma sequência de estados em tal que:
- a concatenação dos símbolos das transições entre esses estados resulte na palavra em questão;
- a sequência acabe num estado final.
Exemplo de Palavra Aceite num AFND
Consideremos o AFND que aceita todas as palavras com número ímpar de 's ou que terminam em :
Ora, tentemos então verificar se algumas palavras são ou não aceites por este autómato:
-
tenhamos ; não deve ser aceite: não tem número ímpar de 's nem termina em . As imagens abaixo procuram seguir a sequência de estados da palavra. Nenhuma delas termina num estado final, pelo que a palavra não é aceite (como esperado).
-
por outro lado, consideremos - a palavra deve ser aceite, já que tem número ímpar de 's. Vejamos então o caminho percorrido ao ler a palavra:
Como último passo, lemos aqui o símbolo vazio - podemos sempre lê-lo, e transitamos assim para o estado final desejado!
A linguagem reconhecida por um AFND é o conjunto das palavras aceites por esse AFND, isto é, o conjunto .
Exemplo de Linguagem Reconhecida por um AFND
Por exemplo, a linguagem reconhecida pelo AFND acima é a linguagem das palavras sobre o alfabeto que têm um número ímpares de 's ou acabam em .
Conversão de AFND's em AFD's
Temos que todas as linguagens reconhecidas por AFND's são linguagens regulares. Por outras palavras, seja qual for o AFND, existe um AFD que reconhece a mesma linguagem que o AFND de partida. Vamos ver daqui para a frente como obter a partir de um AFND o seu AFD equivalente.
Primeiro, começamos por remover os movimentos-:
Dado um AFND , temos que o AFND é-lhe equivalente se
- ;
- é tal que para cada e .
Pode-se entender a função como sendo aplicada a palavras com apenas uma letra.
Desta forma, é claro que (em , considerar os fechos- não tem efeito) pelo que os autómatos e reconhecem a mesma linguagem.
Remoção de movimentos-
Vamos compreender as alterações acima:
- Se podermos alcançar um estado final através de um movimento-, então se considerarmos esse estado como sendo também final, as palavras reconhecidas pelo nosso AFND não mudam;
- Para cada estado vamos ver que estados conseguimos alcançar usando apenas a letra . O conjunto de estados que conseguimos alcançar só com corresponde ao resultado de aplicar a todos os estados em e depois tirar o fecho- do resultado. Isto é, pego em todos os estados a que consigo chegar com , vejo onde consigo chegar com , e finalmente aplico outra vez.
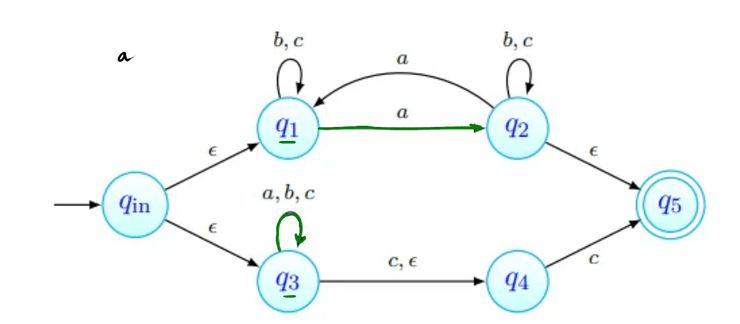
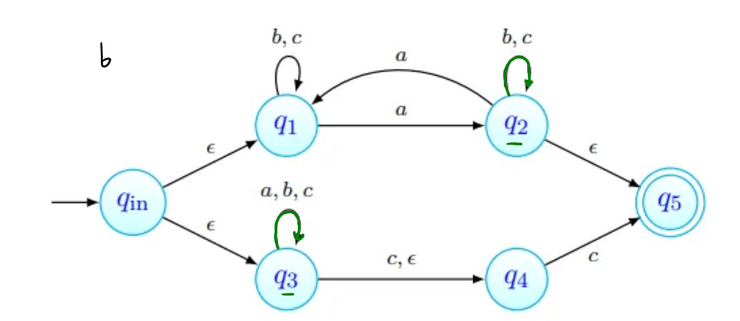
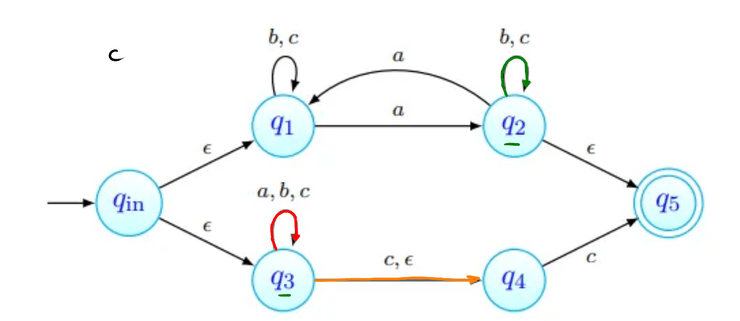
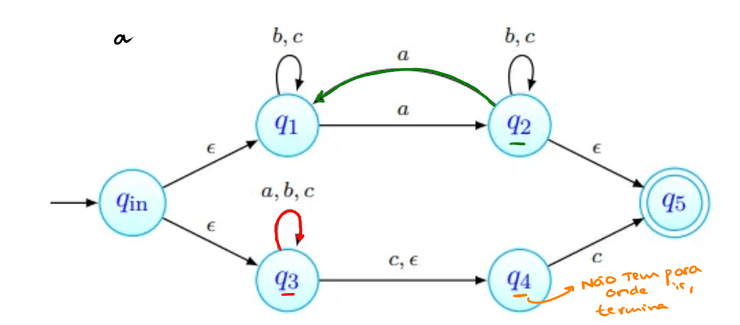
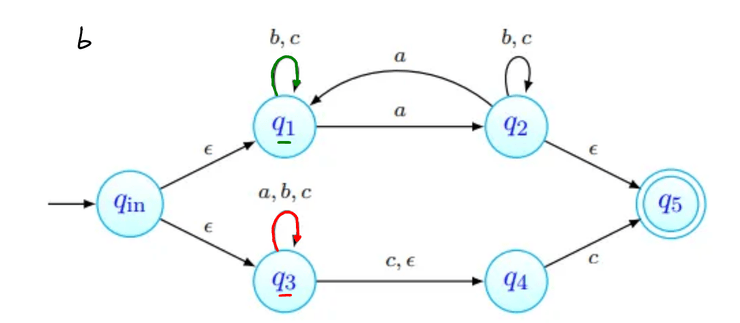
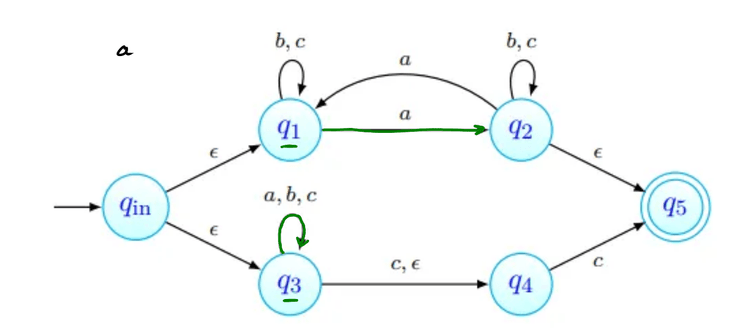
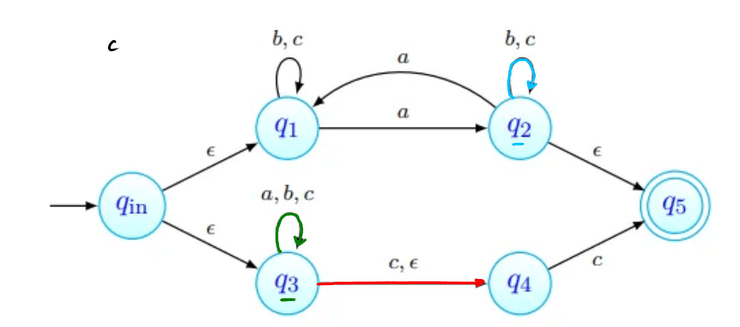
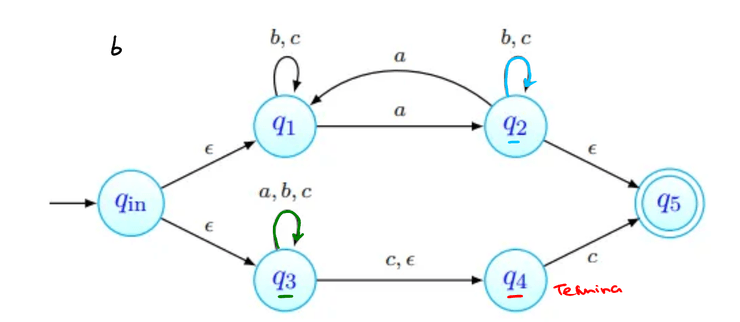
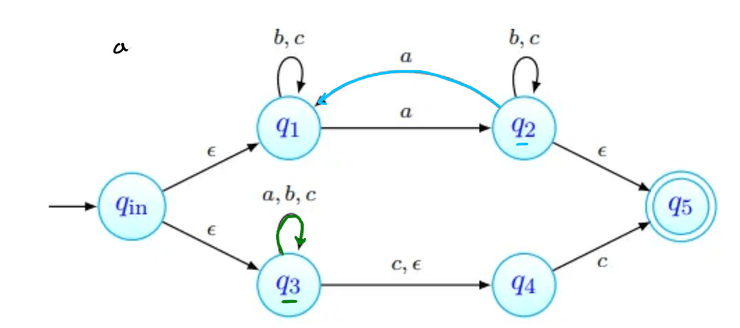
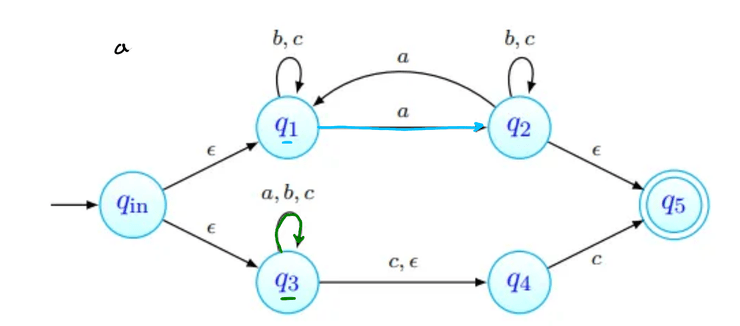
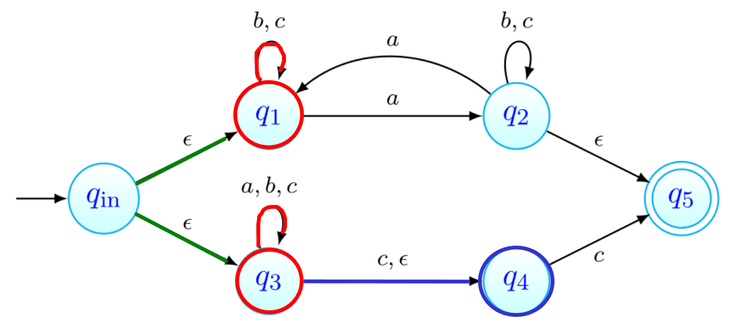
Por exemplo, na imagem acima, estão assinalados que podem ser obtidos a partir de com a letra . Todas as transições a partir de passam por:
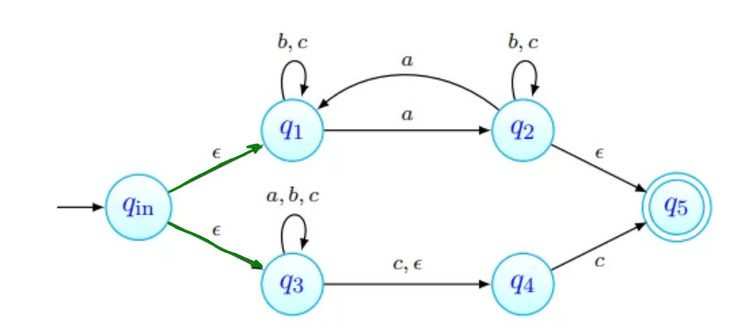
- ver onde é possível chegar com movimentos-. Na nossa imagem, estes primeiros movimentos estão assinalados a verde. O estado , apesar de estar em não está marcado com seta verde pois não há nenhum transição a partir de com .
- depois, fazemos então as transições que usam a letra , transições estas que estão assinaladas com setas vermelhas.
- finalmente, podemos ainda fazer mais movimentos-, que estão assinalados a azul.
Os estados que conseguimos obter a partir de com apenas um são os vermelhos e os azuis - .
Prova da equivalência entre e
A definição de função de transição estendida para o AFND será
em que em cima consideramos o fecho- de em , mas em baixo consideramos o fecho- de em .
Ou seja, a função de transição estendida de é tal que, dada uma letra e um estado , podemos alcançar todos os estados que podíamos em com essa letra (e possivelmente com movimentos-).
Indutivamente, se dermos uma palavra a , obtemos o mesmo conjunto de estados que obtiamos em .
Consequentemente, uma palavra é aceite em se e só se for aceite em .
Cuidado! Esta prova é indutiva com caso base , pelo que só funciona para palavras com pelo menos uma letra.
Isto é, falta provar a equivalência para .
Ora, é aceite em se e só se .
Ora, isto equivale a ser um estado final em , pelo que também é aceite em se e só se for aceite em .
Exemplo da remoção de movimentos-
Em relação à imagem mostrada acima, vamos construir um AFND equivalente sem movimentos- que vamos denominar .
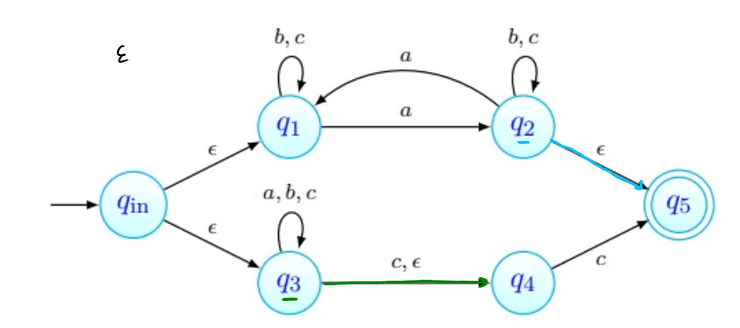
Começamos por ver que a partir de podemos:
- usando chegar a (a partir de ), (também a partir de , usando depois um movimento-), (através de ) e finalmente (através de , usando depois um movimento-).
- usando chegar a (como vimos acima).
- usando chegar a .
O processo de remoção dos movimentos- não passa de identificar estes conjuntos para todos os estados e assinalar as transições correspondentes no novo autómato . Desta forma, vamos então obter o autómato apresentado abaixo.
Note-se que o estado também passou a ser final, como tinha sido dito na teoria. Isto, como já foi explicado, acontece já que todas as palavras que terminem em são aceites (pois podem terminar em com mais um movimento-).
Agora que já não temos movimentos-, passamos o AFND para um AFD:
Dado um AFND , temos que o AFD em que:
- ;
- é tal que, para cada e
reconhece a mesma linguagem que
Observe-se que a função , por ser uma função, está bem definida e é determinística para todo o input.
Isto é, para qualquer input, só pode ter um output.
A questão é que, como vimos na definição, este output está definido em e não em .
O segredo para arranjar um AFD equivalente a um AFND será então identificar os estados de com conjuntos de estados de .
Prova da equivalência entre e
Vamos definir a função de transição estendida de
Consequentemente, se houver tal que , temos que para qualquer tal que .
Verificamos então que se a função nos leva a um estado , a função leva-nos a um estado tal que .
Então, se for final em , temos que e é final em .
Exemplo da passagem de AFND para AFD
Como foi sugerido acima, a passagem para o determinismo é feita através da identificação dos estados do AFD com conjuntos de estados do AFND .
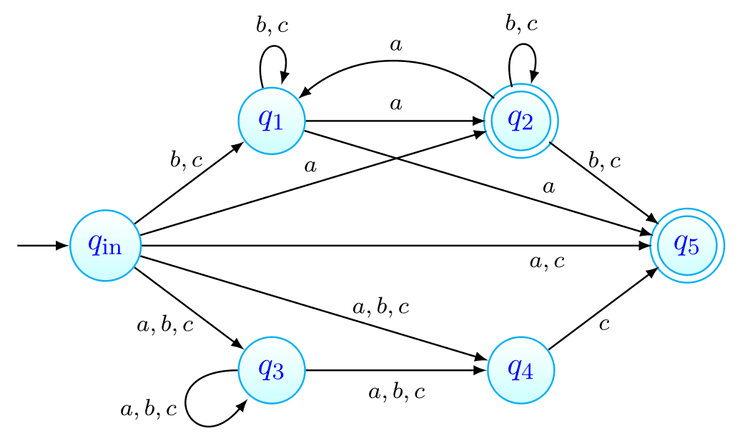
Voltando ao exemplo que temos visto, depois da remoção dos movimentos- ficámos com o AFND
No novo AFD vamos começar com um estado inicial que corresponde ao conjunto .
A partir deste estado, com um é possível chegar aos estados em .
Desta forma, em vai haver um estado correspondente a este conjunto de forma que .
De forma semelhante, haverá estados e de forma que e .
O algoritmo de transição de para limita-se então a repetir este processo para todos os estados que vão aparecendo, até que todos os estados tenham transições definidas para as letras do alfabeto que se justificam.
Geralmente, procuramos usar uma tabela para nos ajudar na conversão. Os estados representados no AFD final correspondem a todos os estados a que podemos chegar a partir do estado inicial, ao olhar para a tabela.
O preenchimento da tabela é muito simples: um par linha-coluna corresponde a um par estado-símbolo, onde o conteúdo da entrada da tabela correspondente está associado ao conjunto de estados a que podemos aceder partindo desse estado e transicionando através desse símbolo.
Não é preciso incluir todas as linhas da tabela que foram incluídas: fizemo-lo por completude, mas só precisamos de representar os estados a que podemos chegar a partir do estado inicial.
Neste caso, por exemplo, após podíamos representar logo na tabela e não , depois , etc.
O autómato resultante desta conversão será o seguinte:
Acabamos só por reparar que enquanto os AFD's têm a vantagem de terem todas as transições bem determinadas, podem necessitar de bastante mais estados que um AFND equivalente.
Nomeadamente, se for um AFND com conjunto de estados com elementos, o AFD mínimo que lhe corresponde pode ter até estados (o conjunto de estados de está contido em ).
Desta forma, os AFND's podem ser frequentemente uma forma mais eficiente de representar a mesma linguagem.
No entanto, como temos algoritmos para converter AFND's em AFD's, podemos dizer ao computador para fazer esse trabalho chato.
Propriedades das Linguagens Regulares
A classe das linguagens regulares é muito bem comportada, suportando uma quantidade de construções. Comecemos por analisar as suas propriedades lógicas.
Proposição
Para um alfabeto e linguagens regulares, temos que e são linguagens regulares.
Prova
Seja um AFD que reconhece . Temos então que o AFD reconhece a linguagem , pelo que esta é também regular. Ao AFD damos o nome de AFD dual de .
Sejam e AFD's tais que e .
Definimos o AFD produto como o AFD cuja função tal que, para cada e :
É fácil de observar que .
Corolário
É imediato a partir da proposição acima que se e são regulares, então, por exemplo, e também o são.
Prova
.
Proposição
Para um alfabeto e , temos que e são também linguagens regulares.
Prova para
Sejam e AFD's tais que e .
Considere-se o AFND com função de transição tal que,
Podemos observar que reconhece .
Entenda-se da seguinte forma:
- inicialmente estamos em . Podemos escolher começar por ler palavras em , e vamos para , ou em , e vamos para .
- Quando acabamos de ler uma palavra em podemos:
- ir para se quisermos ler mais palavras em ;
- ir para se quisermos começar a ler palavras em .
- Sempre que acabamos de ler uma palavra em :
- ou acabamos e aceitamos a palavra lida;
- ou voltamos para para ler mais uma palavra de $L_2.
Prova para
Considere-se um AFD que reconheça a linguagem . Seja o AFND para um estado tal que
e é tal que, para cada e :
É fácil de perceber que reconhece , pelo que é regular.
Observe-se que o que o AFND oferece é um autómato que a acrescenta a possibilidade de começarmos a ler uma nova palavra reconhecida por , sempre que estivermos num estado de aceitação (mudando para o estado ).
O estado é de aceitação pois a palavra vazia também está em .
Expressões Regulares
Para um alfabeto definimos o conjunto das expressões regulares sobre como o conjunto definido indutivamente como se segue:
- ;
- para cada ;
- se , então (soma);
- se , então (concatenação);
- se , então (fecho de Kleene).
Para simplificar vamos ocultar os parêntesis quando desnecessários, e vamos abreviar por .
Dada uma expressão regular , definimos a linguagem denotada por como o conjunto definido indutivamente como se segue:
- ;
- para cada ;
- ;
- ;
- .
Duas expressões regulares dizem-se equivalentes () se denotarem a mesma linguagem.
Proposições para expressões regulares
Sobre expressões regulares, verificam-se as seguintes propriedades:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
A relevância das expressões regulares neste contexto vem da seguinte proposição:
Proposição
Uma linguagem é regular se e só se houver uma expressão regular que a denote.
Prova
Que a linguagem denotada por uma expressão regular é também regular é imediato a partir da definição de expressão regular, de linguagem denotada por expressão regular, e das propriedades em relação a operações sobre expressões regulares.
Para qualquer AFD, é possível reescrevê-lo como um sistema de equações lineares, que podemos resolver como vamos ver a seguir.
Solução de uma Equação Linear com Expressões Regulares
Para resolver sistemas de equações com expressões regulares, observamos que a equação
tem como solução a expressão regular .
Desta forma, podemos resolver um sistema de equações com variáveis tal como fazemos nos números reais.
Ver o exemplo abaixo para perceber como.
Exemplo de Resolução de Sistemas de Equações
Considere-se o seguinte AFD:
Podemos traduzir o AFD no seguinte sistema de equações:
Note-se como o sistema acima tem equações (uma para cada estado) e variáveis (também uma para cada estado).
Vemos agora que a terceira equação é linear em , pelo que podemos substituir diretamente pela solução.
Ficamos agora também com uma equação linear em :
A expressão correspondente ao estado inicial é então , pelo que esta denota a linguagem reconhecida pelo AFD.
Lema de Pumping
Para mostrar que uma linguagem não é regular, há que garantir que não existe nenhum autómato finito que a reconheça, ou expressão regular que a denote. A seguinte proposição enuncia um resultado, conhecido como Lema de Pumping ou Lema da bombagem (para AFD's), que é útil para esse efeito:
Se é uma linguagem regular, então existe tal que, se é uma palavra com então em que são tais que:
- ;
- ;
- para cada .
Prova
Seja uma linguagem regular, onde , para um AFD .
Seja e uma palavra de com .
Quando o autómato recebe a palavra lê letras e portanto passa por estados.
Se na leitura de , passamos por pelo menos estados, temos que, segundo o Teorema de Pombal, há um estado pelo qual passamos duas vezes.
Seja o primeiro estado que é repetido. Chamemos então à palavra que é lida até à primeira ocorrência de , à palavra que é lida entre as primeiras duas ocorrências de , e à restante palavra.
Temos então que
- , porque ainda não se repetiu estados
- , uma vez que podemos apenas repetir as transições de estados que acontecem entre as duas ocorrências de quantas vezes quisermos.
Exemplo do Lema de Pumping
Vamos usar o Lema de Pumping para provar que a linguagem não é regular.
Assuma-se que a linguagem é regular.
Segundo o Lema de Pumping, existem, para algum , tal que tais que:
- ;
- ;
- para cada .
Considere-se uma palavra com . Como , esta palavra está na condição do Lema. Como , temos que e para . Consequentemente, temos que também pertence à linguagem .
Contudo isto é claramente um absurdo, pelo que a linguagem em questão não é regular.
Autómato de Pilha
Um autómato de pilha (AP) (em inglês push-down automaton) é um tuplo em que:
- é um alfabeto;
- é um alfabeto auxiliar;
- é um conjunto finito não vazio de estados;
- é o estado inicial;
- é o conjunto de estados finais;
Explicando de forma mais simples, um autómato de pilha é um AFND ao qual se adiciona uma estrutura adicional: uma pilha.
Nesta estrutura podemos, em cada transição, adicionar e remover um símbolo do alfabeto auxiliar (incluindo símbolos vazios).
Desta forma, a função de transição deve ser entendida seguinte:
quer dizer que quando estamos num estado , lemos uma letra na palavra e verificamos que se encontra um símbolo , podemos transitar para o estado , substituindo o símbolo na pilha pelo símbolo .
Se a letra lida na pilha for , a transição de para pode ser feita para qualquer estado da pilha. Devemos então colocar o símbolo no topo da pilha.
Simetricamente, se , quer dizer que devemos apenas remover o símbolo que estava na pilha, sem colocar nenhum novo.
Vamos agora formalizar o conceito de palavra aceite por um AP.
Compreendemos que a pilha acumula símbolos do alfabeto auxiliar , pelo que podemos representá-la por uma palavra em .
Definimos então uma palavra aceite por um AP como uma palavra tal que:
- pode ser escrita como , com ;
- existem uma sequência de estados e uma sequência de pilhas com e para cada tais que:
- e ;
- com , para e algum ;
- .
A linguagem reconhecida por um AP , denotada corresponde ao conjunto de palavras aceites por .
As linguagens que são reconhecidas por AP's são denominadas de linguagens independentes do contexto, que abreviamos para ou apenas quando o alfabeto está subentendido ou é irrelevante no contexto.
Temos que , isto é, todas as linguagens regulares são independentes de contexto, havendo linguagens que são independentes de contexto, mas não são regulares.
Prova
Que , uma vez que um autómato de pilha é uma generalização de um AFD. Para fazer um AP que reconheça qualquer basta considerar o AP que é igual ao AFD que reconhece , em que nenhuma transição mexe na pilha.
Que é também evidente: já vimos acima pelo menos uma linguagem que é independente de contexto, mas não é regular (a linguagem das palavras ).
Propriedades das Linguagens Independentes do Contexto
As linguagens independentes do contexto mantêm algumas boas propriedades das linguagens regulares, mas perdem algumas. Vamos agora ver exatamente quais das propriedades são preservadas.
Proposição
Para um alfabeto e linguagens independentes do contexto, temos que , e são linguagens independentes do contexto.
Prova
As provas passam, tal como fizemos nas linguagens regulares, por pegar em autómatos que reconhecem as linguagens , e , e construir um autómato que reconheça a linguagem que queremos provar que é independente de contexto.
Resumidamente, ficam as ideias para construir os autómatos:
- Para , considerar como fizemos antes um autómato produto (fica para pensar o que é preciso fazer com a pilha);
- Para considerar uma composição dos autómatos e : quando estamos num estado final de , podemos fazer um movimento- para o estado inicial de , assinalando esta transição na pilha com um símbolo especial;
- Para considerar a composição acima do AP para si próprio: em cada estado final de adicionamos um movimento- para o estado inicial, marcando também esta transição na pilha com um símbolo especial.
Lamentamos a brevidade da prova. Aceitam-se contribuições.
No entanto, no geral, a classe das linguagens independentes do contexto não é fechada para intersecções ou complementações. Não temos ainda um método para verificar que uma linguagem não é independente do contexto. Tal como para as linguagens regulares, isto é feito através do Lema de Pumping, mas desta vez da sua versão para autómatos de pilha.
Lema de Pumping para Linguagens Independentes do Contexto
Se é uma linguagem do contexto, então existe tal que se é uma palavra com , então em que satisfazem as seguintes condições:
- , ou seja ;
- ;
- , para qualquer .
Aplicação do Lema de Pumping
Vamos usar o Lema de Pumping para Linguagens Independentes para provar que a linguagem não é independente.
A prova é bastante semelhante à que não é regular.
No entanto, aqui, vamos ter de considerar vários casos:
Para o cuja existência é garantida pelo Lema, consideramos a palavra . Uma de três coisas acontece:
- tem apenas b's;
- tem pelo menos um a, e não tem nenhum c;
- tem pelo menos um c, e não tem nenhum a. Em qualquer um dos casos, podemos ver que a palavra não tem o mesmo número de a's, b's e c's, pelo que a linguagem não pode ser independente de contexto.