Diferenciabilidade

Ponto Fixo de uma Função

Exemplo - TVI para descobrir o ponto fixo de uma função

Considere-se, agora, uma função $f : [0, 1] \rightarrow [0, 1]$, contínua. Sendo g a função definida por

$$g : [0, 1] \rightarrow \R , g(x) = f(x) − x,$$

$g$ é contínua, por ser a diferença de duas funções contínuas,

$$\begin{array}{c} g(0) = f(0) ≥ 0 \wedge g(1) = f(1) − 1 ≤ 0. \end{array}$$

Então, uma das três afirmações é verdadeira:

• $g(0) = 0$ e, portanto, $f(0) = 0$, logo $f$ tem um ponto fixo em 0;
• $g(1) = 0$ e, portanto, $f(1) = 1$, logo $f$ tem um ponto fixo em 1;
• $g(1) < 0 < g(0)$ e, pelo TVI, o contradomínio de $g, g([0, 1])$, contém o intervalo

$$[g(1), g(0)] \ni 0,$$

logo $g$ tem um zero e, nesse ponto, $f$ tem um ponto fixo.
Como é óbvio, em qualquer um dos casos $f$ tem um ponto fixo.

Exemplo - Weierstrass para descobrir o ponto fixo de uma função

Seja, agora,

$$f : \R \rightarrow \R , f(x) = \frac{e^x - 1}{e^x + 1},$$

Como $f$ é contínua em $\R$, existe uma vizinhança de cada ponto em $\R$ na qual $f$ é limitada. Como a reunião de infinitos conjuntos limitados não tem que ser, e em geral não é, limitada, não é possível, contudo, garantir, deste modo, que $f$ é limitada.
Por outro lado, a existência de

$$f(−\infty) = \lim_{x \rightarrow -\infty} \frac{e^x - 1}{e^x + 1} = -1 \in \R$$

garante que existe um $R_1 \in \R^+$ tal que $f$ é limitada em $V_{R_1}(- \infty) = ] - \infty, -\frac{1}{R_1} [$.

Método da Bissecção

Ao utilizar o TVI, este método permite diminuirmos o intervalo onde pode estar o ponto que pretendermos verificar que pertence ao contra domínio de uma função. Para quem conhece, este método funciona de forma semelhante à binary search.

Funciona da seguinte maneira:

1. Dividir o intervalo (e.g. $[-1, 1]$) ao meio ($[-1, 0]$ e $[0, 1]$)
2. Ver em que intervalo (ou ambos), aplicando o TVI, se situa o valor que queremos provar que existe pela função $f$.
3. Repetir até ter um intervalo do tamanho desejado.

Exemplo

Tomemos a função $g$, e queremos provar que tem um zero:

$$g:[0, 1]\rightarrow \R\quad,\quad g(x)=e^x-5x^2$$

Descobrimos os valores de $0$ e $1$ e aplicamos o TVI:

$$g(0)=1>0\quad g(1)=e-5<0$$

Logo, $g$ contém um zero no seu domínio, mas conseguimos melhorar o intervalo em que estamos a procurar, aplicando o método da bisseção.

$$g(0.5)=\sqrt e - \frac 5 4 >0$$

Logo, pelo TVI, há pelo menos um zero de $g$ em $[0.5, 1]$. Mas podemos continuar a melhorar:

$$g(0.7)=e^{0.7}-2.45 <0$$

Logo, há pelo menos um zero de $g$ em $[0.5, 0.7]$.

Podemos repetir este processo até termos um intervalo suficientemente pequeno, de acordo com o que pretendermos.

Distância de um ponto a um conjunto compacto

Sejam $X\subset\R$ um compacto e $x_0\in\R$. Chama-se distância de $x_0$ a $X$ ao mínimo da função:

o qual é sempre um número não negativo. A distância de $x_0$ a $X$ é nula se e só se $x_0\in X$.

Razão incremental

É útil estudar a variação de uma função para ser possível determinar os máximos e mínimos de uma função.

Assim, define-se a razão incremental de $f$ no intervalo $[x,y]$, a partir da noção de taxa média de variação:

Sendo $f$ uma função real de variável real, $x,y\in D_f\land x\ne y$.

No entanto, esta razão incremental, como se trata de um valor médio, pode esconder variações locais da função.

Introduz-se assim um novo conceito, em que $y=x_0$ fixo e faz-se o limite da razão incremental quando $x\rightarrow x_0$. Ao valor deste limite chama-se taxa de variação instantânea ou derivada de $f$ no ponto $x_0$:

com $R\in\R^+$.

Derivada de uma função num ponto

Sejam $D_f \subset \R$, $f : D_f \rightarrow \R$ e $x_0 \in \text{int } D_f$. Chama-se derivada de $f$ no ponto $x_0$ ao limite

caso este exista.

• Se o limite existir e for finito, a função diz-se diferenciável em $x_0$.
• Se o limite existir em $\overline\R$, $f$ diz-se derivável no ponto $x_0$.
• Se o limite não existir, $f$ diz-se não derivável no ponto $x_0$.

Chama-se domínio de diferenciabilidade de $f$ ao conjunto $D_{f'}\subset\text{int }D_f$ de todos os pontos onde a derivada de $f$ existe e é finita.

Uma função diferenciável num ponto, é também, obviamente, derivável nesse ponto. O contrário (recíproco) não se verifica.

Outra forma de escrever este limite é com:

Exemplos de cálculos de derivadas

Exemplo 1

Como primeiro exemplo, considere-se a função polinomial definida por

$$f : \R \rightarrow \R , f(x) = a_1 x + a_0,\quad a_1, a_0 \in \R \wedge x_0 \in \R.$$

A derivada no ponto $x_0$ é o limite

$$f'(x_0) = \lim_{x\rightarrow x_0} \frac{(a_1 x + a_0) − (a_1 x_0 + a_0)}{x - x_0} = \lim_{x\rightarrow x_0} a_1 = a_1.$$

Então, o domínio de diferenciabilidade de $f$ é $\R$ e a derivada em cada ponto $x_0$ $\in \R$ é

$$f'(x_0) = a_1.$$

Constata-se, assim, que $f$ é uma função contínua e diferenciável em todo o seu domínio.

Exemplo 2

Considere-se, agora, a função g definida por

$$g : \R \rightarrow \R , g(x) = \sqrt[3]{x}$$

e $x_0 \in \R$. A derivada no ponto $x_0$ é o limite

$$g'(x_0) = \lim_{x\rightarrow x_0} \frac{\sqrt[3]{x} − \sqrt[3]{x_0}}{x - x_0} = \lim_{x\rightarrow x_0} \frac{x − x_0}{(x - x_0)(\sqrt[3]{x^2} + \sqrt[3]{x_0 x} + \sqrt[3]{x^2_0})} = \frac{1}{3 \sqrt[3]{x^2_0}},$$

se $x_0 \neq 0$. No caso de $x_0 = 0$, o limite ainda existe, pois o denominador tem sinal fixo, mas vale $+ \infty$, logo não é finito. Então, o domínio de diferenciabilidade de $g$ é $\R \backslash \{0\}$ e a derivada em cada ponto $x_0 \in \R \backslash \{0\}$ é

$$g'(x_0) = \frac{1}{3 \sqrt[3]{x^2_0}}.$$

A função $g$ é uma função contínua e derivável em $\R$, mas só é diferenciável em $R \backslash \{0\}$.

Exemplo 3

Para estudar um caso em que a derivada não existe porque a razão incremental tem dois limites finitos distintos, estuda-se a função definida por

$$g_2 : \R \rightarrow \R, \quad g_2(x) = |x|$$

e $x_0 \in \R$. A derivada no ponto $x_0$ é o limite

$$g'_2(x_0) = \lim_{x\rightarrow x_0} \frac{|x| - |x_0|}{x - x_0} = \lim_{x \rightarrow x_0} \frac{x^2 - x^2_0}{(x - x_0)(|x| + |x_0|)} = \frac{x_0}{|x_0|},$$

se $x_0 \neq 0$. Neste caso, para $x_0 = 0$ o limite não existe, pois os limites laterais correspondentes têm valores diferentes: o limite à direita vale 1 e o à esquerda vale −1. Então, o domínio de diferenciabilidade de $g_2$ é $\R \backslash \{0\}$ a a derivada em cada ponto $x_0 \in \R \backslash \{0\}$ é

$$g'_2(x_0) = \frac{x_0}{|x_0|},$$

ou seja, é 1 se $x_0 > 0$ e −1 se $x_0 < 0$. A função $g_2$ é uma função contínua em $\R$ mas só é diferenciável e derivável em $R \backslash \{0\}$.

Exemplo 4

Por fim, estuda-se uma função que não é contínua, a função de Heaviside, definida por

$$h : \R \rightarrow \R , \quad h(x) = \begin{cases} 1 \quad \text{ se } x > 0\\ \frac{1}{2} \quad \text{ se } x = 0\\ 0 \quad \text{ se } x < 0 \end{cases},$$

e $x_0 \in \R$. Se $x_0 > 0$, a derivada no ponto $x_0$ é o limite

$$f'(x_0) = \lim_{x\rightarrow x_0} \frac{1 - 1}{x - x_0} = 0,$$

já que a função verifica $h(x) = 1$ numa vizinhança de $x_0$.
De modo em tudo semelhante, se $x_0 < 0$, a derivada também é 0. Se $x_0 = 0$, tem-se

$$\lim_{x\rightarrow 0^+} \frac{1 - \frac{1}{2}}{x} = + \infty \quad {e} \quad \lim_{x\rightarrow 0^-} \frac{0 - \frac{1}{2}}{x} = + \infty$$

logo o limite que dá a derivada existe e é $+ \infty$.
Então, o domínio de diferenciabilidade de $h$ é $\R \backslash \{0\}$ e a derivada em cada ponto $x_0 \in \R \backslash \{0\}$ é

$$h'(x_0) = 0.$$

A função $h$ é uma função contínua e diferenciável em $\R \backslash \{0\}$ e é derivável em $\R$, apesar de ser descontínua em 0.

Reta Tangente ao gráfico de uma função

Sejam $D_f\subset\R$, $f:D_f\rightarrow\R$ e $x_0\in \text{int }D_f$.

• Se existir e for finita a derivada (diferenciável) de $f$ em $x_0$, $f'(x_0)$, chama-se reta tangente ao gráfico de $f$ no ponto $(x_0, f(x_0))$ à reta de equação

• Se a derivada existir mas for infinita (derivável, mas infinita), a reta tangente define-se como sendo a reta vertical de equação

• Se não existir derivada (não derivável), diz-se que não existe reta tangente ao gráfico de $f$ nesse ponto.

Ponto semi-interior

Seja $A\subset\R$ e $x_0\in A$.

• Diz-se que $x_0$ é um ponto semi-interior à direita, de $A$, se o intervalo $[x_0,x_0+r[$ estiver contido em $A$, para algum $r\in\R^+$.
• Diz-se que $x_0$ é um ponto semi-interior à esquerda, de $A$, se o intervalo $]x_0-r;x_0]$ estiver contido em $A$, para algum $r\in\R^+$.
  Exemplo

  Considerando um intervalo $A=[3,5]$. O conjunto dos pontos interiores deste conjunto é $\text{int }A=]3,5[$. No entanto, o ponto $x=3$ é um ponto semi-interior à direita, pois $[3,3+r[$ pertence a $A$ para algum $r\in \R^+$. Do mesmo modo, o ponto $x=5$ é um ponto semi-interior à esquerda, pois $]5-r, 5]$ pertence a $A$ para algum $r\in \R^+$.

Semi-vizinhança

Tal como se falou de pontos semi-interiores, também de pode falar de semi-vizinhanças:

• Chama-se de semi-vizinhança direita de $x_0$, de raio $r\in\R^+$, ao intervalo $[x_0,x_0 + r[$.
• Chama-se de semi-vizinhança esquerda de $x_0$, de raio $r\in\R^+$, ao intervalo $]x_0-r,x_0]$.

Derivada Lateral num ponto

Com o conceito de pontos semi-interiores, podemos assim definir as derivadas laterais num ponto:

Sejam $D_f\subset\R$, $f:D_f\rightarrow\R$ e $x_0\in D_f$.

• Se $x_0$ é um ponto semi-interior à direita de $D_f$, chama-se derivada à direita de $f$ no ponto $x_0$ ao limite, caso este exista,

• Se $x_0$ é um ponto semi-interior à esquerda de $D_f$, chama-se derivada à esquerda de $f$ no ponto $x_0$ ao limite, caso este exista,

Propriedades da diferenciabilidade e derivabilidade

• Existem funções que são contínuas e não são deriváveis, por exemplo o módulo.
• Existem funções que são deriváveis e não são contínuas, por exemplo a função de Heaviside.
• Todas as funções estudadas que são diferenciáveis num ponto também são contínuas nesse ponto.
• A noção de diferenciabilidade é mais útil que a de derivabilidade.
• Qualquer função diferenciável num ponto é necessariamente contínua nesse ponto.

Regras da Derivação

Sejam $D_f,D_g\subset\R$, $f:D_f\rightarrow\R$, $g:D_g\rightarrow\R$, $x_0\in(\text{int }D_f\cap\text{int }D_g)$ e $\alpha \in\R$.

• $(f+g)'(x_0)=f'(x_0)+g'(x_0)$
• $(\alpha f)'(x_0)=\alpha f'(x_0)$
• $(f\cdot g)'(x_0)=f'(x_0)g(x_0)+f(x_0)g'(x_0)$
• Com $f(x_0)\ne 0$ ; $\displaystyle\bigg(\frac gf\bigg)'(x_0)=\frac{f(x_0)g'(x_0)-f'(x_0)g(x_0)}{f^2(x_0)}$
• Com $f(a)>0$ ; $(f^\alpha)'(a)=\alpha f'(a)f^{\alpha-1}(a)$
• Com $f(a)\in\text{int }D_g$ ; $(g\circ f)'(a)=g'(f(a))\cdot f'(a)$, em que $f$ tem de ser diferenciável em $a$ e $g$ tem de ser diferenciável em $f(a)$.

Tabela com derivadas de funções comuns

Regra de derivação do produto de $n$ termos

Sejam $n\in\N_2$, $D_{f_k}\subset\R$, $f_k:D_{f_k}\rightarrow\R$, $k=1,\dots,n$ e

Então, se $f_k$ é diferenciável em $x_0$, $k=1,\dots,n$, o mesmo se sucede com $\displaystyle f=\prod_{k=1}^nf_k$,

tendo-se

Resumidamente, o que a expressão acima simboliza é que, a derivada de um produto com $n$ fatores é uma soma de $n$ termos em que em cada um deles se deriva só um dos fatores, mantendo os restantes inalterados.

Função Derivada

Após a definição de função derivada, pode-se escrever as regras de derivação com uma notação mais leve, atendendo aos devidos domínios:

• $(f+g)'=f'+g'$
• $(\alpha f)'=\alpha\cdot f'$
• $(f\cdot g)'=f'\cdot g+f\cdot g'$
• $\displaystyle \bigg(\frac g f\bigg)'=\frac{g'\cdot f - g\cdot f'}{f^2}$
• $(f^\alpha)'=\alpha\cdot f'\cdot f^{\alpha-1}$
• $(g\circ f)'=(g'\circ f)\cdot f'$
• $(f^{-1})'=\frac 1{f'\circ f^{-1}}$ (a definir abaixo)

Notação alternativa para derivadas

Podemos assim reescrever a derivada da composta, considerando $y=f(x)$ e $z=g(y)$:

Exemplos de Resoluções de Derivadas

Exemplo 1

$$f : \R \rightarrow \R , \quad f(x) = (1 + x^2)^{12}.$$

O domínio de diferenciabilidade de $f$ é $\R$ e a sua função derivada é

$$f' : \R \rightarrow \R , \quad f'(x) = 12(1 + x^2)^{11} (1 + x^2)' = 24x(1 + x^2)^{11}.$$

Neste exemplo usou-se a regra de derivação da potência.

Exemplo 2

Apresenta-se, agora, um exemplo em que é necessário aplicar diretamente o teorema da composta. Seja $g$ uma função diferenciável na origem e $f$ a função definida numa vizinhança do ponto 1 por

$$f(x) = g(x^3 − 2x + 1).$$

Para calcular $f'(1)$ faz-se

$$f'(x) = g'(x^3 − 2x + 1)(3x^2 − 2),$$

para $x$ numa vizinhança de 1, pelo teorema da composta. Então, $f'(1) = g'(0)$.
O mesmo problema pode ser formalizado usando a notação $\frac{dy}{dx}$. Para tal, definem-se as variáveis $y = x^3 − 2x + 1$ e $z = g(y)$. Como se pretende calcular a derivada no ponto 1, tem-se $x_0 = 1$ e $y_0 = 0$. A cadeia de composição conduz à fórmula

$$\frac{dz}{dx}(1) = \frac{dz}{dy}(0) \cdot \frac{dy}{dx}(1)$$

Como se tem

$$\frac{dz}{dy}(y) = g'(y) \quad \text{e} \quad \frac{dy}{dx}(x) = 3x^2 - 2$$

obtém-se

$$\frac{dz}{dx}(1) = g'(0).$$

Uma das vantagens da noção de função derivada é a de permitir intuitivamente transformar a noção de derivada num ponto, que é pontual numa noção local ou seja definida numa vizinhança do ponto.

Diferenciabilidade local

Este teorema permite-nos transformar a noção de derivada num ponto numa noção local, isto é, que está definida numa vizinhança do ponto.

É de notar que qualquer função que seja diferenciável em todo o seu domínio tem que estar definida num conjunto aberto, visto que apenas se pode verificar a diferenciabilidade local em pontos do interior do domínio.

Classes de funções

Resumidamente, uma função se seja diferenciável duas vezes, será de classe $C^2$, se for diferenciável três vezes, será de classe $C^3$, etc. Se não for diferenciável mas for contínua, diz-se uma função de ordem $C^0$.

Assim:

• Uma função de ordem $C^0$ em $A$ é uma função contínua em $A$
• Uma função de ordem $C^1$ em $A$ é uma função diferenciável em $A$ cuja função derivada é contínua em $A$.
• Para um dado aberto $A$, $C^0(A)\supset C^1(A) \supset C^2(A)\supset \dots\supset C^n(A)\supset \dots$
• Se, para um dado aberto $A$, $f$ é de classe $C^n$ em $A$ para qualquer $n\in\N_0$ diz-se que ${f\in C^\infin (A)}$.

Derivada da Inversa

Apresentam-se duas versões deste teorema - a versão forte, mais correta mas mais difícil de usar, e a versão fraca, mais fácil de aplicar.

A fórmula para a derivada pode ser apresentada de uma forma mais simples:

$(f^{-1})'=\frac 1{f'\circ f^{-1}}$

Derivadas de Funções Elementares

• $(e^u)'=u'e^u$
• $\displaystyle(\log u)'=\frac {u'}u$
• $(\sin u)'=u'\cdot \cos u$
• $(\cos u)'=-u'\cdot\sin u$
• $\displaystyle(\tg u)'=\frac {u'}{\cos^2u}$
• $\displaystyle(\cotg u)'=\frac{-u'}{\sin^2 u}$
• $\displaystyle(\arcsin u)'=\frac {u'} {\sqrt{1-u^2}}$
• $\displaystyle (\arccos u)'=\frac{-u'}{\sqrt{1-u^2}}$
• $\displaystyle(\arctg u)'=\frac{u'}{1+u^2}$
• $\displaystyle(\arcctg u)'=\frac{-u'}{1+u^2}$
• $(\sh u)'=u'\ch u$
• $(\ch u)'=u'\sh u$
• $\displaystyle(\th u)'=\frac{u'}{\ch^2u}$
• $\displaystyle(\coth u)'=\frac{-u'}{\sh^2 u}$
• $\displaystyle(\arg\sh u)'=\frac{u'}{\sqrt{1+u^2}}$
• $\displaystyle(\arg\ch u)'=\frac{u'}{\sqrt{u^2-1}}$
• $\displaystyle(\arg\th u)'=\frac{u'}{1-u^2}$

Introdução ao teorema de Lagrange

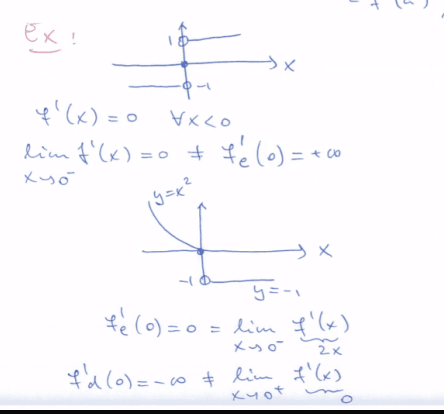
Nas 2 primeiras páginas do PDF da aula 15, apresenta-se o estudo de uma função com um comportamento fora do normal, de onde se retira que:

• Uma função pode ser diferenciável em $\R$ mas não ser de classe $C^1$, pois a sua derivada não é contínua.
• Uma derivada de uma função $f$ num ponto pode ser positiva sem que seja crescente em alguma vizinhança desse ponto
• Uma função derivada pode ser positiva num ponto mas trocar de sinal infinitas vezes em qualquer vizinhança desse ponto
• Pode existir $f'_d(a)$ e $f'_e(a)$ sem existir $f'(a^+)$ e $f'(a^-)$ (como no exemplo abaixo)
• Uma função pode ter derivada nula num ponto mas não ter nenhum extremo nesse ponto

Exemplo

Extremo Local de uma função

Sejam $D_f\subset\R$ e $f:D_f\rightarrow \R$ e $x_0\in D_f$.

• $x_0$ diz-se um maximizante local de $f$ se existe algum $r\in\R^+$ tal que $f(x_0)$ é o máximo de $f\big|_{V_r(x_0)\cap D_f}$. Nesse caso, $f(x_0)$ diz-se um máximo local de $f$. Também se diz que $f$ tem um máximo local em $x_0$.
• $x_0$ diz-se um minimizante local de $f$ se existe algum $r\in\R^+$ tal que $f(x_0)$ é o mínimo de $f\big|_ {V_r(x_0)\cap D_f}$. Nesse caso, $f(x_0)$ diz-se um mínimo local de $f$. Também se diz que $f$ tem um mínimo local em $x_0$.
• $x_0$ diz-se um extremante local de $f$ se $x_0$ é um maximizante local ou um minimizante local de $f$.
• $f(x_0)$ diz-se um extremo local de $f$ se $f(x_0)$ é um máximo local de $f$ ou um mínimo local de $f$.

Daqui podem-se tirar algumas conclusões:

• Se $f$ tem um máximo, esse máximo também é um máximo local. O mesmo para o mínimo.
• Existem funções que têm máximo local num ponto interior do seu domínio sem que tenham derivada nula nesse ponto. A noção de extremo não está dependente da noção de derivada.
• Uma função pode ter derivada nula num ponto mas não ter nenhum extremo nesse ponto.
• Existem funções com extremos locais que não são limitadas. Mesmo que sejam limitadas, o seu supremo/ínfimo pode não ser um dos seus máximos/mínimos locais.

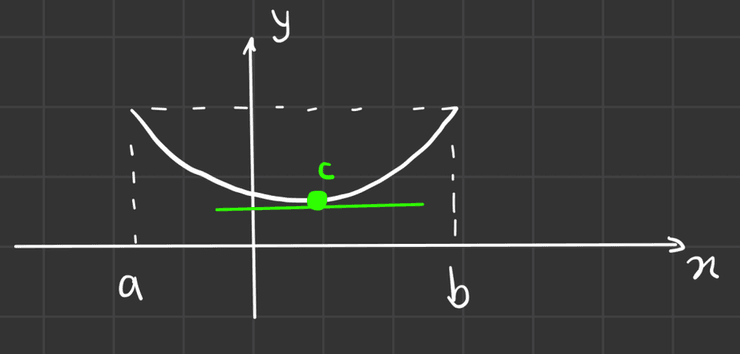
Teorema de Rolle (e aplicações)

É fácil compreender este teorema, se se observar o seguinte esquema:

Este teorema garante que existe pelo menos um ponto c, no entanto, se a função for constante, por exemplo, existem infinitos pontos que satisfazem esta condição.

Este teorema pode ser usado para algo bastante mais útil: podemos afirmar que, entre dois zeros consecutivos de $f'$, existe, no máximo, um zero de $f$.

Exemplo do uso desta propriedade

Considere-se, por exemplo, a função polinomial definida por

$$f(x) = 2x^3 + 15x^2 + 36x + 12.$$

Dado que se trata de uma função polinomial do terceiro grau, sabe-se que tem no máximo três zeros, e que tem pelo menos um. Não se sabe, no entanto, se há um, dois ou três e onde os zeros estão colocados.
No entanto, é fácil determinar a derivada de $f$, que é a função polinomial definida por

$$f'(x) = 6x^2 + 30x + 36 = 6(x^2 + 5x + 6)$$

Recorrendo à fatorização do polinómio do segundo grau conclui-se que $f'$ tem exatamente dois zeros, nos pontos −2 e −3. Como $f(- \infty) = −\infty , f(−3) < 0 , f(−2) < 0 \text{ e } f(+\infty) = +\infty$ , a aplicação do Teorema de Rolle diz que existem:

• no máximo, um zero no intervalo $] − \infty, −3[$;
• no máximo, um zero no intervalo $] − 3, −2[$;
• no máximo, um zero no intervalo $] − 2, +\infty[$.
  Usando, agora, o TVI em conjunto com o Teorema de Rolle verifica-se que, para uma função que tem no máximo um zero num intervalo, esse zero existe se e só se a função troca de sinal nos extremos do intervalo. Conclui-se, então, que não existe nenhum zero nos dois primeiros intervalos pelo que a função só tem um zero e ele se encontra no intervalo $] − 2, + \infty[$.

Como é evidente que $f(0) > 0$, pode até afirmar-se que o único zero de $f$ se encontra no intervalo $] − 2, 0[$, usando exatamente o mesmo raciocínio. Se fosse necessário mais precisão na colocação do zero poder-se-ia aplicar o método da bissecção, já apresentado, para diminuir o comprimento do intervalo onde ele se encontra.
Verificou-se, assim, que o Teorema de Rolle pode revelar-se uma ferramenta crucial na determinação do número de zeros de uma função, bem como na localização desses zeros.

Teorema de Darboux

Deste teorema, pode concluir-se que:

• O Teorema de Darboux é parecido ao Teorema do Valor Intermédio, mas para a derivada e sem exigir continuidade desta (no entanto, exige continuidade da função original).
• Qualquer derivada, mesmo que não contínua, tem a propriedade do valor intermédio.
• Qualquer derivada monótona num intervalo é contínua nesse intervalo.

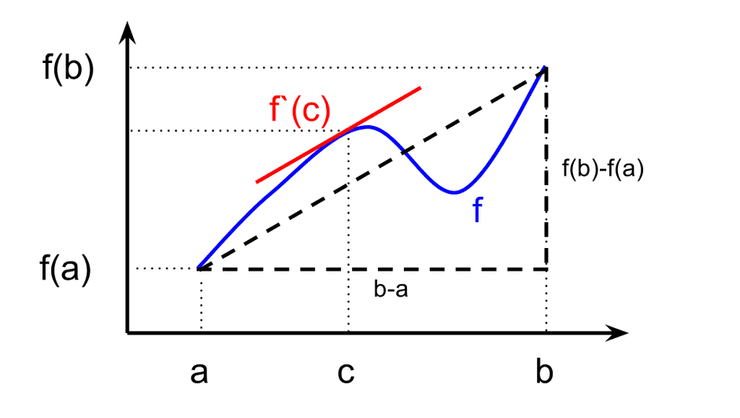
Teorema de Lagrange

Fórmula dos acréscimos finitos

Podemos reescrever o Teorema de Lagrange da seguinte forma:

Substituindo $a$ por $x$ e $b$ por $x_0$:

Se considerarmos um $x$ muito próximo de $x_0$, isto é, um $\Delta x=x-x_0$ muito pequeno e que a derivada de $f$ varia com suficiente lentidão para $f'(c)\approx f'(x_0)$. Então:

Exemplo

Pode-se usar esta fórmula para, por exemplo, calcular o valor aproximado de $\sqrt {102}$.

Arranja-se assim uma função $f(x)=\sqrt x$ e divide-se $102=100+2$, isto é, $x_0=100$ e $\Delta x = 2$.

Então:

$$f(x_0)=f(100)=\sqrt{100}=10\\ f'(x)=(\sqrt x)'=\frac 1 {2\sqrt x}\\ f'(x_0)=f'(100)=\frac 1 {2\sqrt {100}}=\frac 1 {20}$$

Aplicando assim a Fórmula dos Acréscimos Finitos:

$$f(x_0+\Delta x)\approx f(x_0)+f'(x_0)\Delta x\\ \sqrt {102}\approx 10 + \frac 1 {20}\times 2=10.1$$

O que é uma aproximação bastante boa, visto que o valor de $\sqrt{102}\approx 10,099504938$.

Consequências do Teorema de Lagrange

• Se a derivada de uma função existe e é nula num intervalo aberto (não se aplica a pontos), essa função é constante nesse intervalo.
• Se duas funções têm a mesma derivada num intervalo, então a diferença entre elas é uma constante, nesse intervalo.
• Se $f'(x)\ge 0$ num intervalo (relembra-se o exemplo nas duas primeiras páginas do PDF em anexo, que mostra que isto não é válido para pontos), então $f$ é crescente nesse intervalo. Se $f'(x)\le 0$ num intervalo, então $f$ é decrescente nesse intervalo.
• Se $f$ é contínua em $[a,a+r[$ e diferenciável em $]a,a+r[$ para algum $r\in\R^+$, e, para além disso, existe $f'(a^+)$, então existe $f'_d(a)$. No entanto, pode existir $f'_d(a)$ sem existir $f'(a^+)$. O mesmo se aplica para a derivada lateral à esquerda.
• Se $f$ é contínua num intervalo $]a,b[\ni c$ e diferenciável em $]a,b[\backslash\{c\}$, se existir o limite de $f'$ quando $x\rightarrow c$ por valores $x \ne c$ então $f$ é diferenciável em $c$ e $f'$ é contínua em $c$.
• Se $f$ é diferenciável numa vizinhança de $x_0$ e
  $$\lim_{x\rightarrow x_0}\frac{f'(x)}{(x-x_0)^n}=0$$
  então,
  $$\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{(x-x_0)^{n+1}}=0$$

Exemplos - Aplicação do Teorema de Lagrange

Exemplo 1

Considere-se, então a função

$$f : \R \rightarrow \R , f(x) = x e^x.$$

O domínio de diferenciabilidade de $f$ também é $\R$ e a sua derivada pode ser calculada por aplicação das regras de derivação, vindo

$$f': \R \rightarrow \R , \quad f'(x) = e^x + x e^x = (x + 1) e^x.$$

Então, a derivada é não negativa no intervalo $[−1, +\infty[$ e, pelo Teorema de Lagrange (TL), $f$ é crescente nesse intervalo. Por outro lado $f'$ é não positiva no intervalo $] − \infty, −1]$ pelo que $f$ é decrescente nesse intervalo. Conclui-se, portanto que, como $f$ é contínua em −1, tem um mínimo nesse ponto.

Exemplo 2

Como segundo exemplo, utiliza-se o TL para provar que, para qualquer $x > 0$ se tem que

$$e^x > 1 + x.$$

Quando se pretende utilizar o TL para algo deste tipo, o essencial é escolher bem qual a função e qual o intervalo a que se vai aplicar o teorema. Se estas escolhas forem bem feitas, o teorema faz, geralmente, o resto do trabalho, de modo eficiente.
No caso em estudo, o mais natural é aplicar o teorema à função definida por $h(x) = e^x$ no intervalo $[0, x]$. Assim, irão aparecer na expressão que se obtém, $e^x$ e 1, da função calculada nos extremos do intervalo, e $x − 0$, do denominador da expressão dada pelo TL.
Seja, então, $x > 0$ e $h$ a função definida no intervalo $[0, x]$ por $h(x) = e^x$. $h$ é uma função regular no intervalo $[0, x]$ pelo que o teorema de Lagrange permite afirmar que existe um $c \in ]0, x[$ tal que

$$e^c = \frac{e^x − e^0}{x-0} \leftrightarrow \quad \text{e} \quad e^c = \frac{e^x −1}{x}.$$

Como, para $c\in \R^+, e^c > 1$ vem

$$\frac{e^x −1}{x} > 1 \leftrightarrow e^x > x + 1,$$

pois $x > 0$.

---

PDFs:

• Aula 13
• Aula 14
• Aula 15